2023-2024学年人教版数学八年级上册12.2三角形全等的判定(ASA、AAS) 强化练习(含解析)
文档属性
| 名称 | 2023-2024学年人教版数学八年级上册12.2三角形全等的判定(ASA、AAS) 强化练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 355.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 13:44:57 | ||
图片预览



文档简介
三角形全等的判定(ASA、AAS)
一、单选题
1、如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A. B. C. D.
2、如图,D是AB上一点,DF交AC于点E,,.与CE的数量关系是( )
A. B. C. D.无法确定
3、如图,AD是的角平分线,,垂足为E,交ED的延长线于点F,若BC恰好平分,.给出下列四个结论:
①;
②;
③;
④,
其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
4、把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A在桌面上,若另外两个顶点分别距离桌面5cm和3cm,过另外两个顶点向桌面作垂线,则垂足之间的距离,即DE的长为( )cm.
A.6 B.5 C.4 D.8
5、如图,在中,,,AD是经过A点的一条直线,且B、C在AD的两侧,于D,于E,交AB于点F,,,则DE的长为( )
A.6 B.5 C.4 D.8
6、如图,在中,,,垂足分别为D、E,AD、CE交于点H,已知,,则CH的长是( )
A. B.1 C.3 D.2
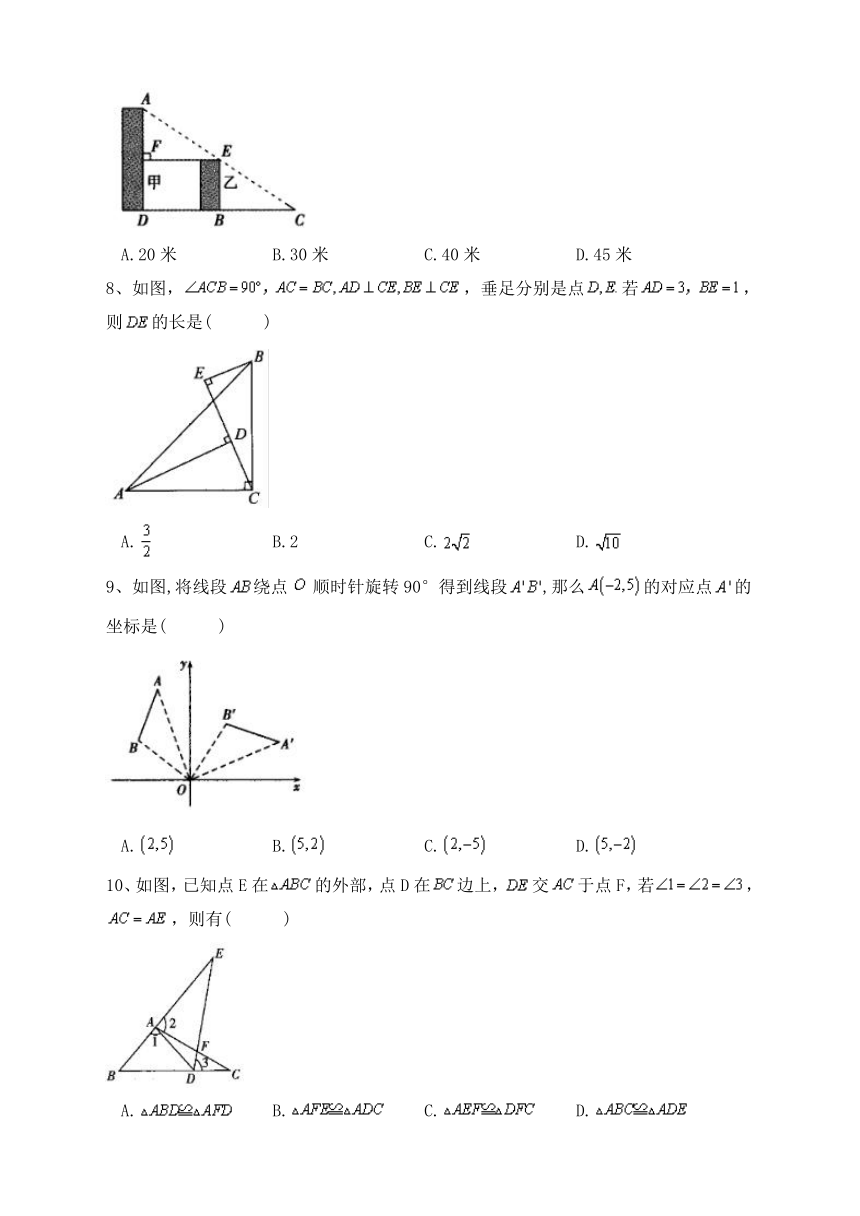
7、如图,小明站在点C处看甲、乙两楼楼顶上的点A和点E.已知C,E,A三点在同一条直线上,B,C相距20米,D,C相距40米,乙楼高BE为15米,小明身高忽略不计,,,则甲楼高AD为( )
A.20米 B.30米 C.40米 D.45米
8、如图,,垂足分别是点若,则的长是( )
A. B.2 C. D.
9、如图,将线段绕点顺时针旋转90°得到线段,那么的对应点的坐标是( )
A. B. C. D.
10、如图,已知点E在的外部,点D在边上,交于点F,若,,则有( )
A. B. C. D.
11、如图,要测量河两岸相对的两点的距离,先在的垂线上取两点,使,再作出的垂线,使在一条直线上,可以说明最恰当的理由是( )
A. B. C. D.
12、如图,在中,,M为BC的中点,H为AB上一点,过点C作,交HM的延长线于点G,若,,则四边形ACGH周长的最小值是( )
A.18 B.9 C.13 D.14
二、填空题
13、已知,如图,在中,,,,,则ED的长为_______cm.
14、如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使,再从点C观测,在BA的延长线上测得一点D,使,这时量得,则水池宽AB是______m.
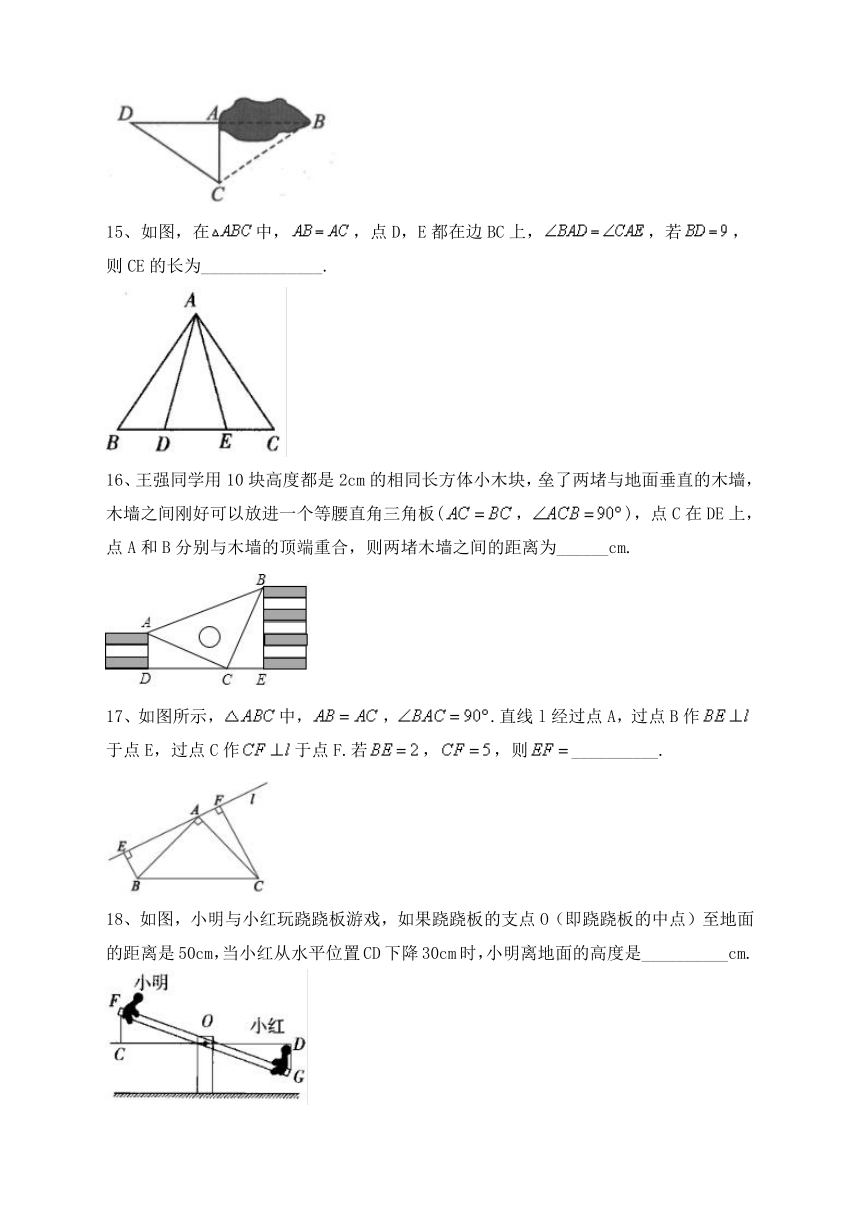
15、如图,在中,,点D,E都在边BC上,,若,则CE的长为______________.
16、王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.
17、如图所示,中,,.直线l经过点A,过点B作于点E,过点C作于点F.若,,则__________.
18、如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是__________cm.
三、解答题
19、如图,在四边形ABCD中,,连接BD,点E在BD上,连接CE,若,.
(1)求证:.
(2)若,,求的度数.
20、如图,在中,点D是上一点,且,,,连接交于点F.
(1)若,求的度数;
(2)若平分,求证:.
21、已知:四边形ABCD中,对角线AC与BD相交于点O,,.
(1)如图1,过点A作交BD于点E,求证:;
(2)如图2,将沿AB折叠,点D的对应点为,求证:.
22、如图,中,,的角平分线AD、BE相交于点P,过P作交BC的延长线于点F,交AC于点H.
(1)求的度数;
(2)求证:;
(3)求证:.
参考答案
1、答案:B
解析:破玻璃保留了原来三角形的两个角和一边,则可以根据来配一块一样的玻璃,
故选:B.
2、答案:A
解析:,.,,,.
3、答案:A
解析:,
,
BC平分,
,
,
,
AD是的角平分线,
,故②③正确;
在与中
,
,
,,故①正确
,故④正确
故选A.
4、答案:D
解析:为等腰三角形,.,,,.在和中,,,,,cm.
5、答案:A
解析:,,
,
于E,
,
,
在与中,
,
,
,,
.
故选:A.
6、答案:B
解析:,,
,
,
,
在和中,
,
,
,
则.
故选:B.
7、答案:B
解析:根据题意,得,所以.因为,所以.易知米,所以,所以(AAS),所以米,因为米,所以米.故选B.
8、答案:B
解析:,
在和中,
,
,
.故选B.
9、答案:B
解析:线段绕点顺时针旋转90°得到线段,
,
.
作轴于,轴于,
.
,
,
.
在和中,
,
,
.
,
,
,
.故选B.
10、答案:D
解析:,即,.故选D.
11、答案:B
解析:略
12、答案:D
解析:,
,
M是BC的中点,
,
在和中,
,
,
,,
,,
四边形ACGH的周长,
当GH最小时,即时四边形ACGH的周长有最小值,
,,
,
,
四边形ACGH的周长最小值为,
故选:D.
13、答案:2
解析:在和中,
,
,
,
,,
,
,
故答案为:2.
14、答案:100
解析:,
,
,,
,
,
故答案为:100.
15、答案:9
解析:,是等腰三角形,.在和中,,,.故答案为9.
16、答案:20
解析:解:由题意得:,,,,
,
,,
,
在和中,,
;
由题意得:cm,cm,
(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
17、答案:7
解析:由题意可知,,,
,
,
,
,
,
在和中,
,
,
,,
,
,,
,
故答案为:7.
18、答案:80
解析:在与中,,,(cm),小明离地面的高度是(cm),故答案为80.
19、答案:(1)见解析;
(2);
解析:(1)证明:,
,
在和中,
,
,
.
(2),,
,
,
.
20、答案:(1)
(2)证明见解析
解析:(1)解:,,,
,
又,
.
(2)证明:平分,
,
,
,
又,
,即:,
在和中,
,
.
21、答案:(1)见解析
(2)见解析.
解析:(1)证明:
,
,,
在和中,
,
;
,,
,,
,
(2)证明:由(1)知,,
,
,
,
即,
,
.
22、答案:(1)AD平分,BE平分,
,,,
,
.
(2)证明:,,
,,.
BE平分,.
在和中,,
.
(3)证明:,
,,.
,,即.
在和中,,
,,
,,
,即.
一、单选题
1、如图,有一块三角形玻璃,小明不小心将它打破.带上这块玻璃,能配成同样大小的一块,其理由是( )
A. B. C. D.
2、如图,D是AB上一点,DF交AC于点E,,.与CE的数量关系是( )
A. B. C. D.无法确定
3、如图,AD是的角平分线,,垂足为E,交ED的延长线于点F,若BC恰好平分,.给出下列四个结论:
①;
②;
③;
④,
其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
4、把等腰直角三角形的三角板按如图所示的方式立在桌面上,顶点A在桌面上,若另外两个顶点分别距离桌面5cm和3cm,过另外两个顶点向桌面作垂线,则垂足之间的距离,即DE的长为( )cm.
A.6 B.5 C.4 D.8
5、如图,在中,,,AD是经过A点的一条直线,且B、C在AD的两侧,于D,于E,交AB于点F,,,则DE的长为( )
A.6 B.5 C.4 D.8
6、如图,在中,,,垂足分别为D、E,AD、CE交于点H,已知,,则CH的长是( )
A. B.1 C.3 D.2
7、如图,小明站在点C处看甲、乙两楼楼顶上的点A和点E.已知C,E,A三点在同一条直线上,B,C相距20米,D,C相距40米,乙楼高BE为15米,小明身高忽略不计,,,则甲楼高AD为( )
A.20米 B.30米 C.40米 D.45米
8、如图,,垂足分别是点若,则的长是( )
A. B.2 C. D.
9、如图,将线段绕点顺时针旋转90°得到线段,那么的对应点的坐标是( )
A. B. C. D.
10、如图,已知点E在的外部,点D在边上,交于点F,若,,则有( )
A. B. C. D.
11、如图,要测量河两岸相对的两点的距离,先在的垂线上取两点,使,再作出的垂线,使在一条直线上,可以说明最恰当的理由是( )
A. B. C. D.
12、如图,在中,,M为BC的中点,H为AB上一点,过点C作,交HM的延长线于点G,若,,则四边形ACGH周长的最小值是( )
A.18 B.9 C.13 D.14
二、填空题
13、已知,如图,在中,,,,,则ED的长为_______cm.
14、如图,要测量水池宽AB,可从点A出发在地面上画一条线段AC,使,再从点C观测,在BA的延长线上测得一点D,使,这时量得,则水池宽AB是______m.
15、如图,在中,,点D,E都在边BC上,,若,则CE的长为______________.
16、王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点C在DE上,点A和B分别与木墙的顶端重合,则两堵木墙之间的距离为______cm.
17、如图所示,中,,.直线l经过点A,过点B作于点E,过点C作于点F.若,,则__________.
18、如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降30cm时,小明离地面的高度是__________cm.
三、解答题
19、如图,在四边形ABCD中,,连接BD,点E在BD上,连接CE,若,.
(1)求证:.
(2)若,,求的度数.
20、如图,在中,点D是上一点,且,,,连接交于点F.
(1)若,求的度数;
(2)若平分,求证:.
21、已知:四边形ABCD中,对角线AC与BD相交于点O,,.
(1)如图1,过点A作交BD于点E,求证:;
(2)如图2,将沿AB折叠,点D的对应点为,求证:.
22、如图,中,,的角平分线AD、BE相交于点P,过P作交BC的延长线于点F,交AC于点H.
(1)求的度数;
(2)求证:;
(3)求证:.
参考答案
1、答案:B
解析:破玻璃保留了原来三角形的两个角和一边,则可以根据来配一块一样的玻璃,
故选:B.
2、答案:A
解析:,.,,,.
3、答案:A
解析:,
,
BC平分,
,
,
,
AD是的角平分线,
,故②③正确;
在与中
,
,
,,故①正确
,故④正确
故选A.
4、答案:D
解析:为等腰三角形,.,,,.在和中,,,,,cm.
5、答案:A
解析:,,
,
于E,
,
,
在与中,
,
,
,,
.
故选:A.
6、答案:B
解析:,,
,
,
,
在和中,
,
,
,
则.
故选:B.
7、答案:B
解析:根据题意,得,所以.因为,所以.易知米,所以,所以(AAS),所以米,因为米,所以米.故选B.
8、答案:B
解析:,
在和中,
,
,
.故选B.
9、答案:B
解析:线段绕点顺时针旋转90°得到线段,
,
.
作轴于,轴于,
.
,
,
.
在和中,
,
,
.
,
,
,
.故选B.
10、答案:D
解析:,即,.故选D.
11、答案:B
解析:略
12、答案:D
解析:,
,
M是BC的中点,
,
在和中,
,
,
,,
,,
四边形ACGH的周长,
当GH最小时,即时四边形ACGH的周长有最小值,
,,
,
,
四边形ACGH的周长最小值为,
故选:D.
13、答案:2
解析:在和中,
,
,
,
,,
,
,
故答案为:2.
14、答案:100
解析:,
,
,,
,
,
故答案为:100.
15、答案:9
解析:,是等腰三角形,.在和中,,,.故答案为9.
16、答案:20
解析:解:由题意得:,,,,
,
,,
,
在和中,,
;
由题意得:cm,cm,
(cm),
答:两堵木墙之间的距离为20cm.
故答案是:20.
17、答案:7
解析:由题意可知,,,
,
,
,
,
,
在和中,
,
,
,,
,
,,
,
故答案为:7.
18、答案:80
解析:在与中,,,(cm),小明离地面的高度是(cm),故答案为80.
19、答案:(1)见解析;
(2);
解析:(1)证明:,
,
在和中,
,
,
.
(2),,
,
,
.
20、答案:(1)
(2)证明见解析
解析:(1)解:,,,
,
又,
.
(2)证明:平分,
,
,
,
又,
,即:,
在和中,
,
.
21、答案:(1)见解析
(2)见解析.
解析:(1)证明:
,
,,
在和中,
,
;
,,
,,
,
(2)证明:由(1)知,,
,
,
,
即,
,
.
22、答案:(1)AD平分,BE平分,
,,,
,
.
(2)证明:,,
,,.
BE平分,.
在和中,,
.
(3)证明:,
,,.
,,即.
在和中,,
,,
,,
,即.
