山东省济南市莱芜区鲁教版八年级下册 期末模拟测试题(含答案)
文档属性
| 名称 | 山东省济南市莱芜区鲁教版八年级下册 期末模拟测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 336.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 08:57:34 | ||
图片预览




文档简介
八年级数学下册期末模拟试题一
一、选择题(10*4=40)
1.下列等式成立的是( )
A.3+4=7 B.×= C.÷=2 D.=3
2.将一元二次方程x2-8x-5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是( )
A.-4,21 B.-4,11 C.4,21 D.-8,69
3.在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
4.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
5.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是( )
A.-7 B.7 C.3 D.-3
6.正方形具有菱形不一定具有的性质是( )
A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等
7.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1 250个迅速增加到第三季度的1 800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到 个( )
A.2 140 B.2 160 C.2 180 D.2 200
8.如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是 ( )
A.= B.BC2=AB·BC C.= D.≈0.618
9.(2020·姑苏区一模)如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
10.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC,BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确的个数是( )
A.4 B.3 C.2 D.1
9. 10.
二、选择题(6*4=24)
11.使式子有意义的x的取值范围是 .
12.若(m-2)+x-3=0是关于x的一元二次方程,则m的值是 .
13.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ= .
13. 14. 16.
15.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是______.
16.如图,在矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为______.
三、解答题
17.(6分)计算:(7+4)(7-4)-(3-1)2
18.(6分)解方程:3x(2x+3)=4x+6.
19.(6分)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
20.(8分)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
21.(8分)如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
22.(8分)观察下列各式:
=1+=1+, =1+=1+,
=1+=1+,…
1.请用n直接表示上面的规律
2.请利用你发现的规律,计算:
+++…+,
23.(10分)安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2 090元,则这种干果每千克应降价多少元
24.(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
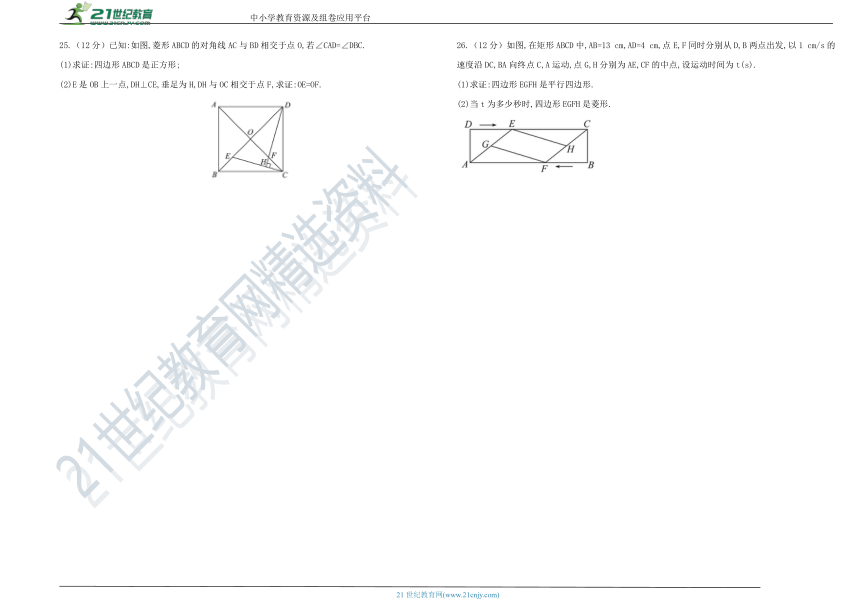
25.(12分)已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形;
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
26.(12分)如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,点G,H分别为AE,CF的中点,设运动时间为t(s).
(1)求证:四边形EGFH是平行四边形.
(2)当t为多少秒时,四边形EGFH是菱形.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
八年级数学下册期末模拟试题一
1.下列等式成立的是( D )
A.3+4=7 B.×=
C.÷=2 D.=3
2.将一元二次方程x2-8x-5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是( A )
A.-4,21 B.-4,11 C.4,21 D.-8,69
3.在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( C )
A.4 B.6 C.8 D.10
4.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( A )
A.3 B.2 C.4 D.5
5.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是( A )
A.-7 B.7 C.3 D.-3
6.正方形具有菱形不一定具有的性质是( D )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
7.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1 250个迅速增加到第三季度的1 800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到 个( B )
A.2 140 B.2 160 C.2 180 D.2 200
8.如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是 ( B )
A.= B.BC2=AB·BC C.= D.≈0.618
9.如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( B )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
10.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC,BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;
②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确的个数是( A )
A.4 B.3 C.2 D.1
11.使式子有意义的x的取值范围是 x< .
12.若(m-2)+x-3=0是关于x的一元二次方程,则m的值是 -2 .
13.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 16
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ= .
15.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是____8____.
16.如图,在矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为___(0,2.1)______.
(0,2.1) 解析:∵矩形OABC中,OA=2,AB=5,∴BC=2,OC=5.∵把△ABC沿着AC对折得到△AB′C,∴B′C=BC,∠B′=∠B=90°,∴AO=CB′,∠AOD=∠B′.又∵∠ADO=∠CDB′,∴△AOD≌△CB′D,∴AD=CD.设OD=x,则AD=CD=5-x.在Rt△AOD中,AD2=OA2+OD2,∴(5-x)2=22+x2,∴x=2.1.∴D点的坐标为(0,2.1).
17.计算:(7+4)(7-4)-(3-1)2
=[72-(4)2]-[(3)2-2×3+1]
=1-(46-6)=-45+6.
18.解方程:3x(2x+3)=4x+6.
3x(2x+3)=2(2x+3),
∴3x(2x+3)-2(2x+3)=0,
∴(2x+3)(3x-2)=0,则2x+3=0或3x-2=0,
解得x=-或x=.
19.已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【解析】(1)∵Δ=(2m+1)2-4×1×(m-2)=4m2+4m+1-4m+8=4m2+9>0,∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系得出,
由x1+x2+3x1x2=1,
得-(2m+1)+3(m-2)=1,解得m=8.
20.如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
【证明】(1)∵四边形ABCD是平行四边形,∴∠A=∠C,
在△AED和△CFD中,∴△AED≌△CFD;
(2)由(1)知△AED≌△CFD,∴AD=DC,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
21.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
【解析】∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°.
∵CE=1,∴DE==.
∵AF⊥DE,∴∠AFD=90°=∠C,∠ADF+∠DAF=90°.
又∵∠ADF+∠EDC=90°,∴∠EDC=∠DAF,
∴△EDC∽△DAF,∴=,即=,
∴FD=,即DF的长度为.
22.(2019·枣庄中考)观察下列各式:
=1+=1+,
=1+=1+,
=1+=1+,…
请利用你发现的规律,计算:
+++…+,
其结果为 2 018 .
23.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0(1)求y与x之间的函数关系式;
(2)商贸公司要想获利2 090元,则这种干果每千克应降价多少元
【解析】(1)设y与x之间的函数关系式为:y=kx+b.
当x=2时,y=120;当x=4时,y=140;
∴,解得:,
∴y与x之间的函数关系式为y=10x+100.
(2)由题意得:(60-40-x)(10x+100)=2 090,
整理得:x2-10x+9=0,解得:x1=1,x2=9,
∵让顾客得到更大的实惠,∴x=9,
答:商贸公司要想获利2 090元,则这种干果每千克应降价9元.
24.(8分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,∴△ADF∽△DEC.
(2)∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得AE===6.
25.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形;
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
【证明】(1)∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,
∴∠BAD=90°,∴四边形ABCD是正方形.
(2)∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,CO=AC,DO=BO,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),∴OE=OF.
26.如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,点G,H分别为AE,CF的中点,设运动时间为t(s).
(1)求证:四边形EGFH是平行四边形.
(2)当t为多少秒时,四边形EGFH是菱形.
【解析】(1)∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=CB,AB∥CD,
∵点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,
∴DE=BF,在△ADE和△CBF中,
∴△ADE≌△CBF,
∴AE=CF,∠DEA=∠CFB,
∵点G,H分别为AE,CF的中点,
∴GE=HF,
∵AB∥CD,∴∠DEA=∠EAF=∠CFB,
∴AE∥CF,∴四边形EGFH是平行四边形.
(2)连接EF,∵四边形EGFH是菱形,G是AE的中点.
∴GF=GE=GA=AE,
∴EF⊥AB,∴DE=AF,
∴t=13-t,∴t=.
即t=s时,四边形EGFH是菱形.
一、选择题(10*4=40)
1.下列等式成立的是( )
A.3+4=7 B.×= C.÷=2 D.=3
2.将一元二次方程x2-8x-5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是( )
A.-4,21 B.-4,11 C.4,21 D.-8,69
3.在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( )
A.4 B.6 C.8 D.10
4.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( )
A.3 B.2 C.4 D.5
5.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是( )
A.-7 B.7 C.3 D.-3
6.正方形具有菱形不一定具有的性质是( )
A.四条边相等 B.对角线互相垂直平分 C.对角线平分一组对角 D.对角线相等
7.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1 250个迅速增加到第三季度的1 800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到 个( )
A.2 140 B.2 160 C.2 180 D.2 200
8.如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是 ( )
A.= B.BC2=AB·BC C.= D.≈0.618
9.(2020·姑苏区一模)如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
10.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC,BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确的个数是( )
A.4 B.3 C.2 D.1
9. 10.
二、选择题(6*4=24)
11.使式子有意义的x的取值范围是 .
12.若(m-2)+x-3=0是关于x的一元二次方程,则m的值是 .
13.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ= .
13. 14. 16.
15.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是______.
16.如图,在矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为______.
三、解答题
17.(6分)计算:(7+4)(7-4)-(3-1)2
18.(6分)解方程:3x(2x+3)=4x+6.
19.(6分)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
20.(8分)如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
21.(8分)如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
22.(8分)观察下列各式:
=1+=1+, =1+=1+,
=1+=1+,…
1.请用n直接表示上面的规律
2.请利用你发现的规律,计算:
+++…+,
23.(10分)安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0
(2)商贸公司要想获利2 090元,则这种干果每千克应降价多少元
24.(10分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
25.(12分)已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形;
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
26.(12分)如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,点G,H分别为AE,CF的中点,设运动时间为t(s).
(1)求证:四边形EGFH是平行四边形.
(2)当t为多少秒时,四边形EGFH是菱形.
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
八年级数学下册期末模拟试题一
1.下列等式成立的是( D )
A.3+4=7 B.×=
C.÷=2 D.=3
2.将一元二次方程x2-8x-5=0化成(x+a)2=b(a,b为常数)的形式,则a,b的值分别是( A )
A.-4,21 B.-4,11 C.4,21 D.-8,69
3.在矩形ABCD中,AC,BD相交于点O,若△AOB的面积为2,则矩形ABCD的面积为( C )
A.4 B.6 C.8 D.10
4.已知△FHB∽△EAD,它们的周长分别为30和15,且FH=6,则EA的长为( A )
A.3 B.2 C.4 D.5
5.已知关于x的一元二次方程x2+5x-m=0的一个根是2,则另一个根是( A )
A.-7 B.7 C.3 D.-3
6.正方形具有菱形不一定具有的性质是( D )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
7.某市发出生活垃圾分类的号召后,实现生活垃圾分类的社区由第一季度的1 250个迅速增加到第三季度的1 800个,照此速度增加,今年第四季度实现生活垃圾分类的社区可以达到 个( B )
A.2 140 B.2 160 C.2 180 D.2 200
8.如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是 ( B )
A.= B.BC2=AB·BC C.= D.≈0.618
9.如图,在平行四边形ABCD中,点E在边DC上,DE∶EC=3∶1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( B )
A.3∶4 B.9∶16 C.9∶1 D.3∶1
10.如图,∠BOD=45°,BO=DO,点A在OB上,四边形ABCD是矩形,连接AC,BD交于点E,连接OE交AD于点F.下列4个判断:①OE平分∠BOD;
②OF=BD;③DF=AF;④若点G是线段OF的中点,则△AEG为等腰直角三角形.正确的个数是( A )
A.4 B.3 C.2 D.1
11.使式子有意义的x的取值范围是 x< .
12.若(m-2)+x-3=0是关于x的一元二次方程,则m的值是 -2 .
13.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 16
14.如图,矩形ABCD中,AB=2,BC=,E为CD的中点,连接AE,BD交于点P,过点P作PQ⊥BC于点Q,则PQ= .
15.△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是____8____.
16.如图,在矩形OABC中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则D点的坐标为___(0,2.1)______.
(0,2.1) 解析:∵矩形OABC中,OA=2,AB=5,∴BC=2,OC=5.∵把△ABC沿着AC对折得到△AB′C,∴B′C=BC,∠B′=∠B=90°,∴AO=CB′,∠AOD=∠B′.又∵∠ADO=∠CDB′,∴△AOD≌△CB′D,∴AD=CD.设OD=x,则AD=CD=5-x.在Rt△AOD中,AD2=OA2+OD2,∴(5-x)2=22+x2,∴x=2.1.∴D点的坐标为(0,2.1).
17.计算:(7+4)(7-4)-(3-1)2
=[72-(4)2]-[(3)2-2×3+1]
=1-(46-6)=-45+6.
18.解方程:3x(2x+3)=4x+6.
3x(2x+3)=2(2x+3),
∴3x(2x+3)-2(2x+3)=0,
∴(2x+3)(3x-2)=0,则2x+3=0或3x-2=0,
解得x=-或x=.
19.已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根;
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【解析】(1)∵Δ=(2m+1)2-4×1×(m-2)=4m2+4m+1-4m+8=4m2+9>0,∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系得出,
由x1+x2+3x1x2=1,
得-(2m+1)+3(m-2)=1,解得m=8.
20.如图,已知四边形ABCD是平行四边形,点E,F分别是AB,BC上的点,AE=CF,并且∠AED=∠CFD.
求证:(1)△AED≌△CFD;
(2)四边形ABCD是菱形.
【证明】(1)∵四边形ABCD是平行四边形,∴∠A=∠C,
在△AED和△CFD中,∴△AED≌△CFD;
(2)由(1)知△AED≌△CFD,∴AD=DC,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
21.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长度.
【解析】∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°.
∵CE=1,∴DE==.
∵AF⊥DE,∴∠AFD=90°=∠C,∠ADF+∠DAF=90°.
又∵∠ADF+∠EDC=90°,∴∠EDC=∠DAF,
∴△EDC∽△DAF,∴=,即=,
∴FD=,即DF的长度为.
22.(2019·枣庄中考)观察下列各式:
=1+=1+,
=1+=1+,
=1+=1+,…
请利用你发现的规律,计算:
+++…+,
其结果为 2 018 .
23.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y(千克)与每千克降价x(元)(0
(2)商贸公司要想获利2 090元,则这种干果每千克应降价多少元
【解析】(1)设y与x之间的函数关系式为:y=kx+b.
当x=2时,y=120;当x=4时,y=140;
∴,解得:,
∴y与x之间的函数关系式为y=10x+100.
(2)由题意得:(60-40-x)(10x+100)=2 090,
整理得:x2-10x+9=0,解得:x1=1,x2=9,
∵让顾客得到更大的实惠,∴x=9,
答:商贸公司要想获利2 090元,则这种干果每千克应降价9元.
24.(8分)如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为点E,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC.
(2)若AB=8,AD=6,AF=4,求AE的长.
【解析】(1)∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C,∴△ADF∽△DEC.
(2)∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,∴=,
∴DE===12.
在Rt△ADE中,由勾股定理得AE===6.
25.已知:如图,菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.
(1)求证:四边形ABCD是正方形;
(2)E是OB上一点,DH⊥CE,垂足为H,DH与OC相交于点F,求证:OE=OF.
【证明】(1)∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,
∴∠BAD+∠ABC=180°,
∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,
∴∠BAD=90°,∴四边形ABCD是正方形.
(2)∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,CO=AC,DO=BO,
∴∠COB=∠DOC=90°,CO=DO,
∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,
∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,
在△ECO和△FDO中,,
∴△ECO≌△FDO(ASA),∴OE=OF.
26.如图,在矩形ABCD中,AB=13 cm,AD=4 cm,点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,点G,H分别为AE,CF的中点,设运动时间为t(s).
(1)求证:四边形EGFH是平行四边形.
(2)当t为多少秒时,四边形EGFH是菱形.
【解析】(1)∵四边形ABCD是矩形,
∴∠D=∠B=90°,AD=CB,AB∥CD,
∵点E,F同时分别从D,B两点出发,以1 cm/s的速度沿DC,BA向终点C,A运动,
∴DE=BF,在△ADE和△CBF中,
∴△ADE≌△CBF,
∴AE=CF,∠DEA=∠CFB,
∵点G,H分别为AE,CF的中点,
∴GE=HF,
∵AB∥CD,∴∠DEA=∠EAF=∠CFB,
∴AE∥CF,∴四边形EGFH是平行四边形.
(2)连接EF,∵四边形EGFH是菱形,G是AE的中点.
∴GF=GE=GA=AE,
∴EF⊥AB,∴DE=AF,
∴t=13-t,∴t=.
即t=s时,四边形EGFH是菱形.
同课章节目录
