25.3 用频率估计概率 课件(共23张PPT)【2023秋人教九上数学高效实用备课】
文档属性
| 名称 | 25.3 用频率估计概率 课件(共23张PPT)【2023秋人教九上数学高效实用备课】 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 23:34:29 | ||
图片预览






文档简介
(共23张PPT)
人教九上数学同步精品课件
人教版九年级上册
25.3 用频率估计概率
第二十五章 概率
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解试验次数较大时试验频率趋于稳定这一规律.
2.结合具体情境掌握如何用频率估计概率.
3.通过概率计算进一步比较概率与频率之间的关系.
学习目标
重点
难点
抛掷一枚硬币,硬币落地后,会出现哪些可能的结果呢?
它们的概率是多少呢?
出现“正面朝上”和“反面朝上”2种情况
都是
思考
新课引入
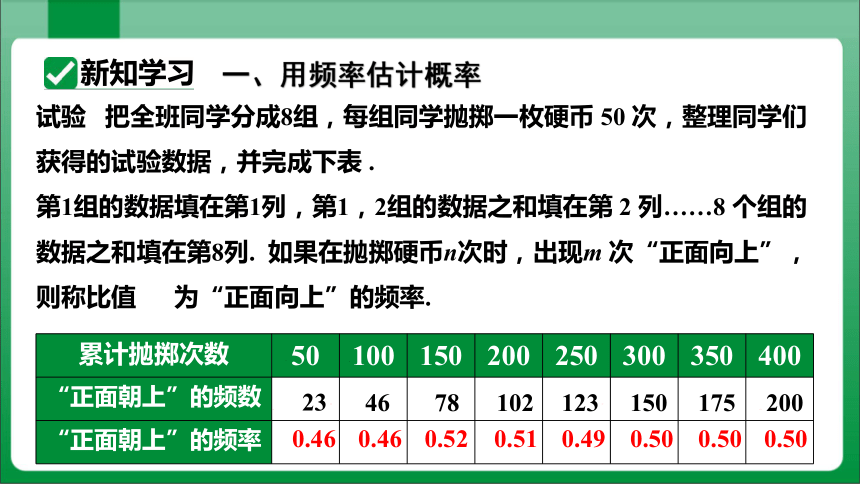
累计抛掷次数 50 100 150 200 250 300 350 400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
试验 把全班同学分成8组,每组同学抛掷一枚硬币 50 次,整理同学们获得的试验数据,并完成下表 .
第1组的数据填在第1列,第1,2组的数据之和填在第 2 列……8 个组的数据之和填在第8列. 如果在抛掷硬币n次时,出现m 次“正面向上”,则称比值 为“正面向上”的频率.
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
一、用频率估计概率
新知学习
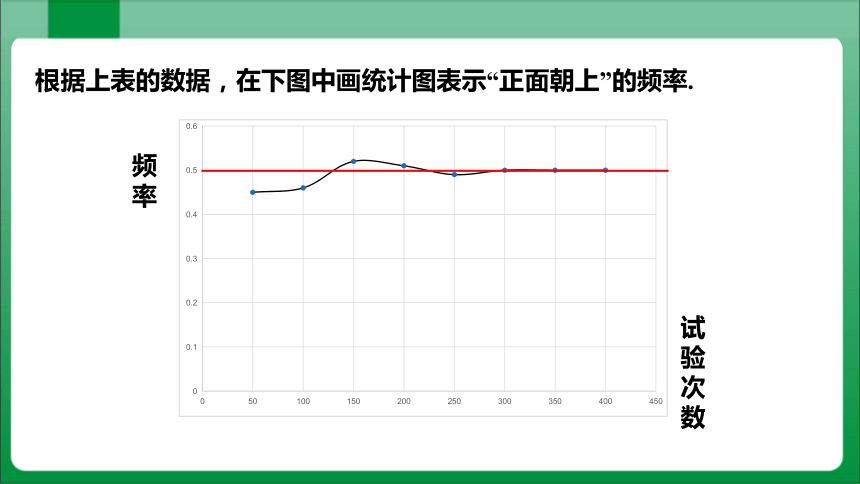
根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
频率
试验次数
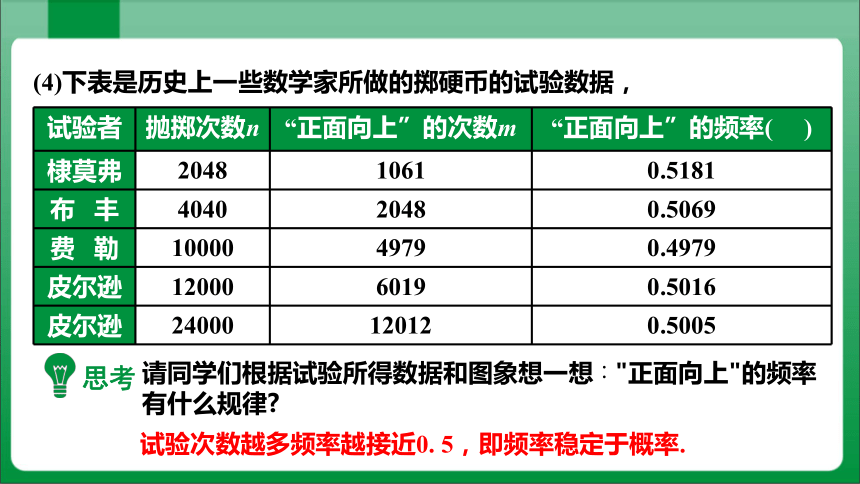
(4)下表是历史上一些数学家所做的掷硬币的试验数据,
试验者 抛掷次数n “正面向上”的次数m “正面向上”的频率( )
棣莫弗 2048 1061 0.5181
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
试验次数越多频率越接近0. 5,即频率稳定于概率.
请同学们根据试验所得数据和图象想一想∶"正面向上"的频率有什么规律
思考
从抛掷硬币的试验还可以发现,"正面向上"的概率是0.5,连续掷2次,结果不一定是"正面向上"和"反面向上"各1次;连续抛掷100次,结果也不一定是"正面向上"和"反面向上"各50次.也就是说,概率是0.5并不能保证掷2n次硬币一定恰好有n次"正面向上",只是当n越来越大时,正面向上的频率会越来越稳定于0.5.
可见,概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
归纳总结
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
频率具有稳定性
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即P(A)=P.
1.判断正误
(1)连续掷一枚质地均匀的硬币10次,结果10次全部是正面,则正面向上的概率是1;
(2)小明掷硬币10000次,则正面向上的频率在0.5附近;
(3)设一大批灯泡的次品率为0.01,那么从中抽取1000只灯泡,一定有10只次品.
×
√
针对训练
×
例 某水果公司以2元/kg的成本价新进10000 kg柑橘.如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
二、用频率估计概率的应用
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在表中. 请你帮忙完成此表.
柑橘总质量n/kg 50 100 150 200 250 300 350 400 450 500
损坏柑橘质量m/kg 5.5 10.5 15.15 19.42 24.25 30.92 35.32 39.24 44.57 51.54
柑橘损坏的频率(结果保册小数点后三位)
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
0.105
0.110
分析:根据上表估计柑橘损坏的概率为0.1,则柑橘完好的概率为0.9.
根据估计的概率可以知道,在 10 000 kg 柑橘中完好柑橘的质量为10000×0.9=9 000 (kg).
设每千克柑橘的售价为 x元,则(x-2.22)×9 000=5 000.解得x≈2.8(元).
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
完好柑橘的实际成本为 (元/kg)
1.某池塘里养了鱼苗10万条,根据这几年的经验知道,鱼苗成活率为95%,一段时间准备打捞出售,第一网捞出40条,称得平均每条鱼重 2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的重量.
解:先计算每条鱼的平均重量是
(2.5×40+2.2×25+2.8×35)÷(40+25+35)=2.53(千克).
所以这池塘中鱼的重量是2.53×100000× 95%=240350(千克).
针对训练
1、一个纸箱内装有除颜色外都相同的80个小球,小明将纸箱里面的小球搅匀后,从中随机摸出一个小球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个小球记下其颜色,把它放回纸箱中,…,多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.3左右,估计该纸箱内红球有________个.
24
随堂练习
2、某校初三一班的学习小组为了体会频率和概率的关系,在一个不透明的盒子里装有红、黄两种颜色的小球共5个(这些小球除颜色外,其他都相同),将小球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复该实验,下表是该小组统计的实验总次数和摸到红球的次数:
实验总次数 10 50 100 200 500 1000
摸到红球的次数 2 23 37 81 198 401
(1)试估计盒子里红、黄两种颜色的小球各有多少个?
解:(1)由表格可知,当实验次数很大时,摸到红球的频率非常接近0.4,
∴估计盒子里红色小球有5×0.4=2(个),黄色小球有5-2=3(个);
(2)该校的小强和小林受“2021西安马拉松赛”的鼓舞,都想报名参加本市田径运动会的“万米长跑”项目,但是只能推选一人参加,小强建议用上述摸球实验(小球的颜色、个数等均不变)来决定由谁参加“万米长跑”项目.规则如下:小强先从盒子里拿出一个小球,不放回,小林再从盒子里拿出一个小球;若两人拿出的小球颜色相同,则小林参加比赛;若两人拿出的小球颜色不同,则小强参加比赛.请你判断谁参加“万米长跑”项目的可能性大,并说明理由.
(2)小强参加“万米长跑”项目的可能性大.列表如下:
小林 小强 红 红 黄 黄 黄
红 (红,红) (黄,红) (黄,红) (黄,红)
红 (红,红) (黄,红) (黄,红) (黄,红)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
由表格知,一共有20种等可能的结果,其中两个小球颜色相同的结果有8种,颜色不同的结果有12种,
∴P(小林)=,P(小强)=
∵<,所以小强参加“万米长跑”项目的可能性大
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教九上数学同步精品课件
人教版九年级上册
25.3 用频率估计概率
第二十五章 概率
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.理解试验次数较大时试验频率趋于稳定这一规律.
2.结合具体情境掌握如何用频率估计概率.
3.通过概率计算进一步比较概率与频率之间的关系.
学习目标
重点
难点
抛掷一枚硬币,硬币落地后,会出现哪些可能的结果呢?
它们的概率是多少呢?
出现“正面朝上”和“反面朝上”2种情况
都是
思考
新课引入
累计抛掷次数 50 100 150 200 250 300 350 400
“正面朝上”的频数
“正面朝上”的频率
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
试验 把全班同学分成8组,每组同学抛掷一枚硬币 50 次,整理同学们获得的试验数据,并完成下表 .
第1组的数据填在第1列,第1,2组的数据之和填在第 2 列……8 个组的数据之和填在第8列. 如果在抛掷硬币n次时,出现m 次“正面向上”,则称比值 为“正面向上”的频率.
23
46
78
102
123
150
175
200
0.46
0.46
0.52
0.51
0.49
0.50
0.50
0.50
一、用频率估计概率
新知学习
根据上表的数据,在下图中画统计图表示“正面朝上”的频率.
频率
试验次数
(4)下表是历史上一些数学家所做的掷硬币的试验数据,
试验者 抛掷次数n “正面向上”的次数m “正面向上”的频率( )
棣莫弗 2048 1061 0.5181
布 丰 4040 2048 0.5069
费 勒 10000 4979 0.4979
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
试验次数越多频率越接近0. 5,即频率稳定于概率.
请同学们根据试验所得数据和图象想一想∶"正面向上"的频率有什么规律
思考
从抛掷硬币的试验还可以发现,"正面向上"的概率是0.5,连续掷2次,结果不一定是"正面向上"和"反面向上"各1次;连续抛掷100次,结果也不一定是"正面向上"和"反面向上"各50次.也就是说,概率是0.5并不能保证掷2n次硬币一定恰好有n次"正面向上",只是当n越来越大时,正面向上的频率会越来越稳定于0.5.
可见,概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
归纳总结
对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量的重复试验,用一个随机事件发生的频率去估计它的概率.
频率具有稳定性
一般地,在大量重复试验中,随机事件A发生的频率 (这里n是实验总次数,它必须相当大,m是在n次试验中随机事件A发生的次数)会稳定到某个常数P.于是,我们用P这个常数表示事件A发生的概率,即P(A)=P.
1.判断正误
(1)连续掷一枚质地均匀的硬币10次,结果10次全部是正面,则正面向上的概率是1;
(2)小明掷硬币10000次,则正面向上的频率在0.5附近;
(3)设一大批灯泡的次品率为0.01,那么从中抽取1000只灯泡,一定有10只次品.
×
√
针对训练
×
例 某水果公司以2元/kg的成本价新进10000 kg柑橘.如果公司希望这些柑橘能够获得利润5000元,那么在出售柑橘(去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?
二、用频率估计概率的应用
销售人员首先从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录在表中. 请你帮忙完成此表.
柑橘总质量n/kg 50 100 150 200 250 300 350 400 450 500
损坏柑橘质量m/kg 5.5 10.5 15.15 19.42 24.25 30.92 35.32 39.24 44.57 51.54
柑橘损坏的频率(结果保册小数点后三位)
0.101
0.097
0.097
0.103
0.101
0.098
0.099
0.103
0.105
0.110
分析:根据上表估计柑橘损坏的概率为0.1,则柑橘完好的概率为0.9.
根据估计的概率可以知道,在 10 000 kg 柑橘中完好柑橘的质量为10000×0.9=9 000 (kg).
设每千克柑橘的售价为 x元,则(x-2.22)×9 000=5 000.解得x≈2.8(元).
因此,出售柑橘时,每千克定价大约2.8元可获利润5000元.
完好柑橘的实际成本为 (元/kg)
1.某池塘里养了鱼苗10万条,根据这几年的经验知道,鱼苗成活率为95%,一段时间准备打捞出售,第一网捞出40条,称得平均每条鱼重 2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,试估计这池塘中鱼的重量.
解:先计算每条鱼的平均重量是
(2.5×40+2.2×25+2.8×35)÷(40+25+35)=2.53(千克).
所以这池塘中鱼的重量是2.53×100000× 95%=240350(千克).
针对训练
1、一个纸箱内装有除颜色外都相同的80个小球,小明将纸箱里面的小球搅匀后,从中随机摸出一个小球记下其颜色,把它放回纸箱中;搅匀后再随机摸出一个小球记下其颜色,把它放回纸箱中,…,多次重复上述过程后,发现摸到红球的频率逐渐稳定在0.3左右,估计该纸箱内红球有________个.
24
随堂练习
2、某校初三一班的学习小组为了体会频率和概率的关系,在一个不透明的盒子里装有红、黄两种颜色的小球共5个(这些小球除颜色外,其他都相同),将小球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复该实验,下表是该小组统计的实验总次数和摸到红球的次数:
实验总次数 10 50 100 200 500 1000
摸到红球的次数 2 23 37 81 198 401
(1)试估计盒子里红、黄两种颜色的小球各有多少个?
解:(1)由表格可知,当实验次数很大时,摸到红球的频率非常接近0.4,
∴估计盒子里红色小球有5×0.4=2(个),黄色小球有5-2=3(个);
(2)该校的小强和小林受“2021西安马拉松赛”的鼓舞,都想报名参加本市田径运动会的“万米长跑”项目,但是只能推选一人参加,小强建议用上述摸球实验(小球的颜色、个数等均不变)来决定由谁参加“万米长跑”项目.规则如下:小强先从盒子里拿出一个小球,不放回,小林再从盒子里拿出一个小球;若两人拿出的小球颜色相同,则小林参加比赛;若两人拿出的小球颜色不同,则小强参加比赛.请你判断谁参加“万米长跑”项目的可能性大,并说明理由.
(2)小强参加“万米长跑”项目的可能性大.列表如下:
小林 小强 红 红 黄 黄 黄
红 (红,红) (黄,红) (黄,红) (黄,红)
红 (红,红) (黄,红) (黄,红) (黄,红)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
黄 (红,黄) (红,黄) (黄,黄) (黄,黄)
由表格知,一共有20种等可能的结果,其中两个小球颜色相同的结果有8种,颜色不同的结果有12种,
∴P(小林)=,P(小强)=
∵<,所以小强参加“万米长跑”项目的可能性大
联系: 频率 概率
事件发生的频繁程度
事件发生的
可能性大小
在实际问题中,若事件的概率未知,常用频率作为它的估计值.
区别:频率本身是随机的,在试验前不能确定,做同样次数或不同次数的重复试验得到的事件的频率都可能不同,而概率是一个确定数,是客观存在的,与每次试验无关.
稳定性
大量重复试验
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
