§30.2.用样本估计总体 2.抽样调查可靠吗?(四川省达川地区达县)
文档属性
| 名称 | §30.2.用样本估计总体 2.抽样调查可靠吗?(四川省达川地区达县) |

|
|
| 格式 | rar | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-27 20:24:00 | ||
图片预览



文档简介
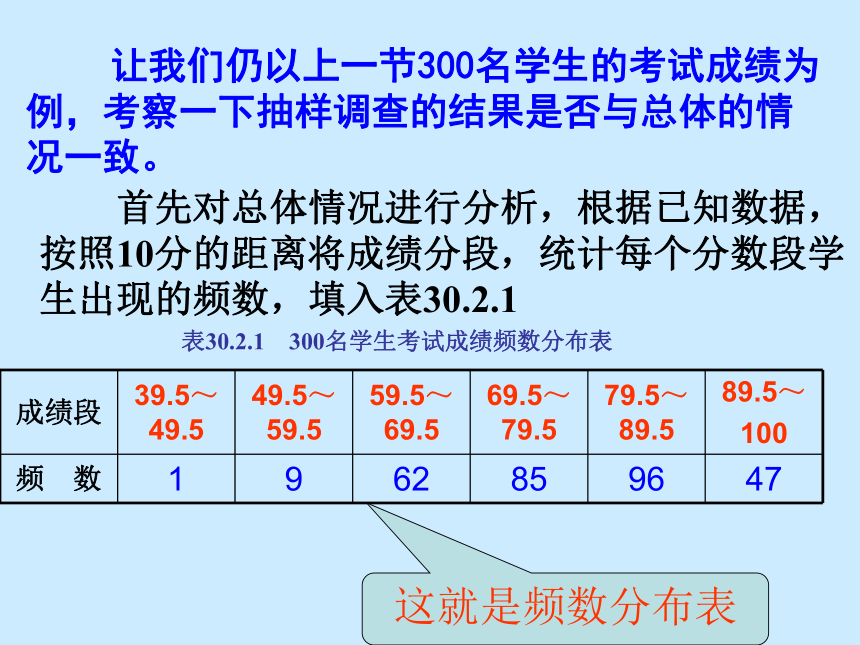
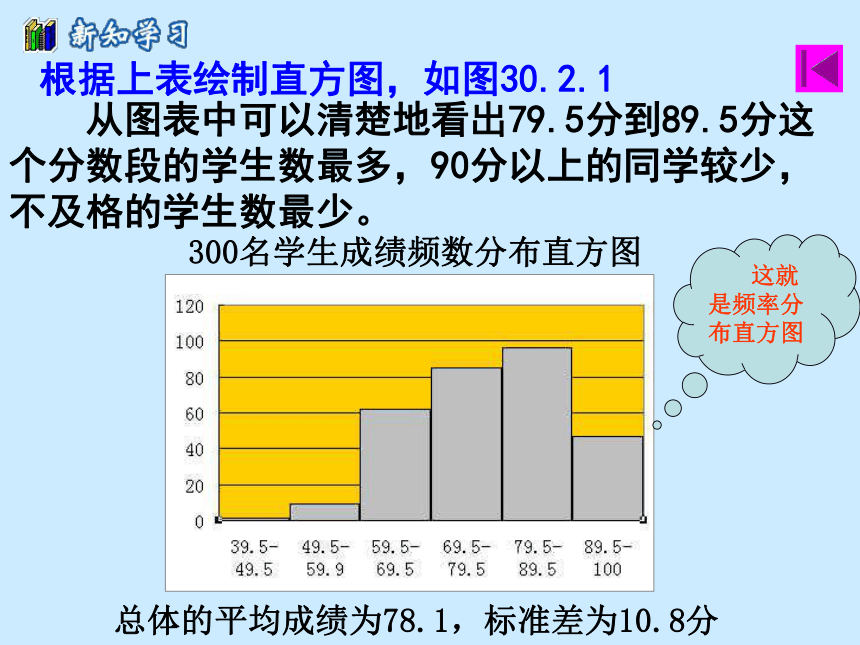
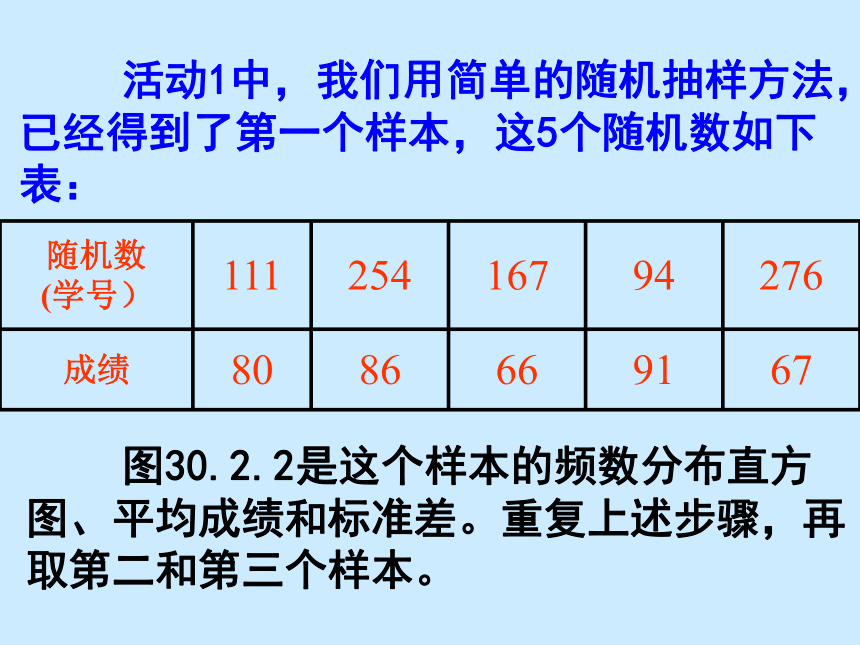
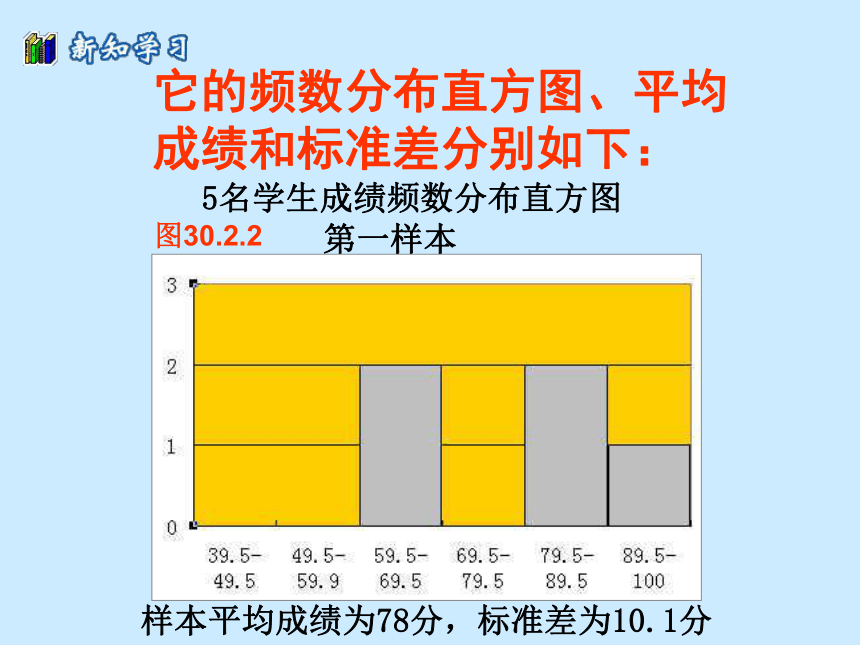
课件24张PPT。用样本估计总体 2. 抽样调查可靠吗?30.2 在上节课中,我们知道在选取样本时应注意的问题,其一是所选取的样本必须具有代表性,其二是所选取的样本的容量应该足够大,这样的样本才能反映总体的特性,所选取的样本才比较可靠. 复习上节课的内容一、 随机抽样调查是了解总体情况的一种重要的数学方法,抽样是它的一个关键,上节课介绍了简单的随机抽样方法,即用抽签的方法来选取样本,这使每个个体都有相等的机会被选入样本. 让我们仍以上一节300名学生的考试成绩为例,考察一下抽样调查的结果是否与总体的情况一致。 首先对总体情况进行分析,根据已知数据,按照10分的距离将成绩分段,统计每个分数段学生出现的频数,填入表30.2.1表30.2.1 300名学生考试成绩频数分布表这就是频数分布表根据上表绘制直方图,如图30.2.1300名学生成绩频数分布直方图总体的平均成绩为78.1,标准差为10.8分 从图表中可以清楚地看出79.5分到89.5分这个分数段的学生数最多,90分以上的同学较少,不及格的学生数最少。 这就是频率分布直方图 活动1中,我们用简单的随机抽样方法,已经得到了第一个样本,这5个随机数如下表: 图30.2.2是这个样本的频数分布直方图、平均成绩和标准差。重复上述步骤,再取第二和第三个样本。它的频数分布直方图、平均
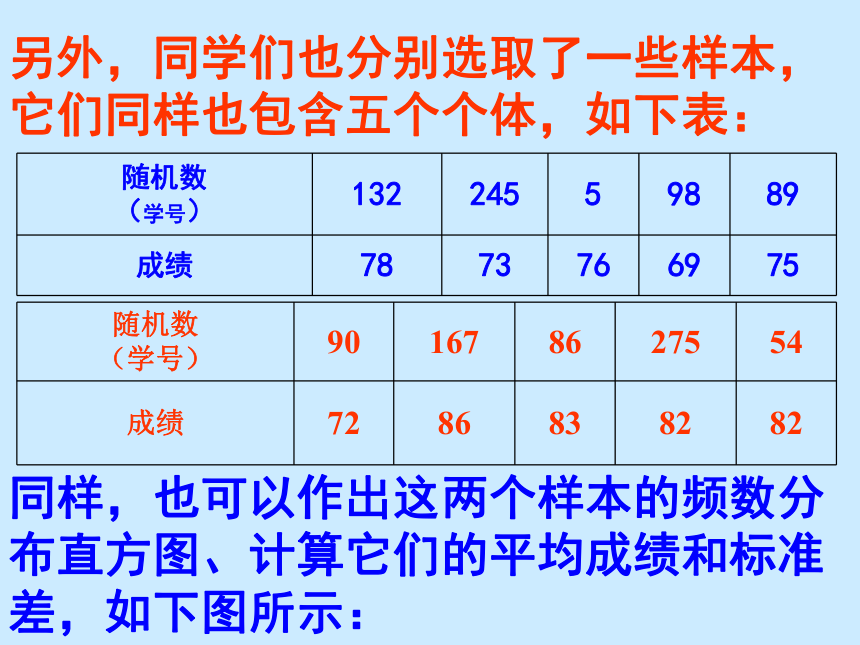
成绩和标准差分别如下:样本平均成绩为78分,标准差为10.1分 图30.2.2另外,同学们也分别选取了一些样本,
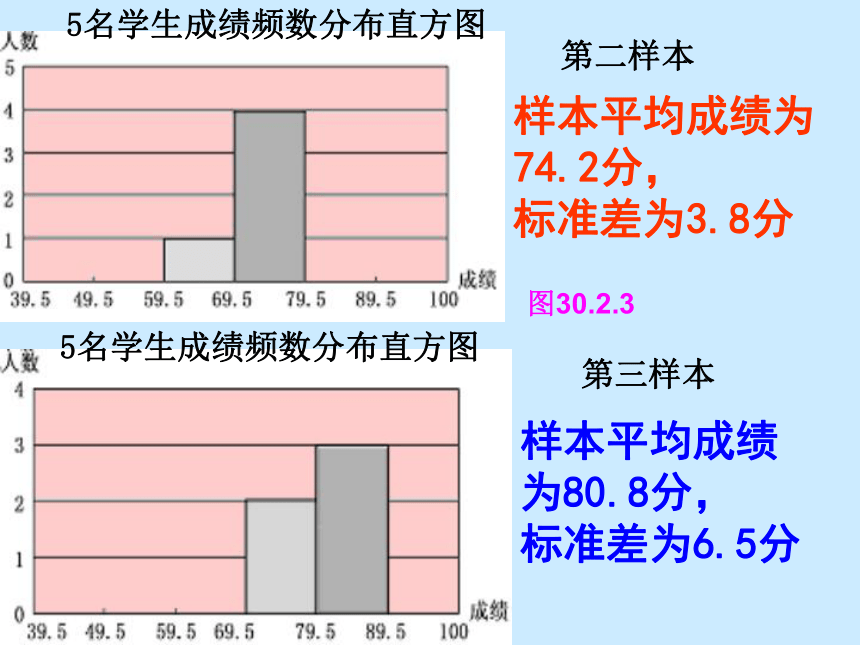
它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和标准差,如下图所示: 样本平均成绩为80.8分,
标准差为6.5分样本平均成绩为
74.2分,
标准差为3.8分 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图图30.2.3 从以上三张图比较来看,它们之间存在
明显的差异,平均数和标准差与总体的平均
数与标准差也相去甚远,显然这样选择的样
本不能反映总体的特性,是不可靠的。样本平均成绩为79.7分,标准差为9.4分 让我们再用大一些的样本试一试,这次每个样本含有10个个体。图30.2.410名学生成绩频数分布直方图第二样本样本平均成绩为83.3分,标准差为11.5分 图30.2.4 我们继续用随机抽样方法,得到第一个样本,重复上述步骤,再取第二个样本。图30.2.4是根据小明取到的样本数据得到的频数分布直方图。 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和标准差似乎比较接近总体的平均成绩78.1分和标准差10.8分。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。图30.2.5是根据小明取到的两个样本数据得到的频数分布直方图。样本平均成绩为75.5分,标准差为10.2分 图30.2.540名学生成绩频数分布直方图第二样本样本平均成绩为77.1分,标准差为10.7分 图30.2.5 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和标准差与总体的平均成绩和标准差的差距更小了!(相当接近总体的平均成绩78.1)你们从自己的抽样过程中是否也得出了同样的结果?选择恰当的样本个体数目样本平均成绩为
75.7分,
标准差为10.2分 样本平均成绩为
77.1分,
标准差为10.7分火星岩石样本 当样本中个体太少时,样本的平均数、标准差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、标准差与总体的标准差相当接近。 三、课堂练习 请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与标准差,绘制频数分布直方图,并与总体的平均数、标准差比较。 为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:练习:(1)在这个问题中,总体、个体、样本和样本容量各是什么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.
解:
(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10(米).
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9(米)和10(米),所以中位数是9.5 (米).样本平均数9.4(米)小结
一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确,相应地,搜集、整理、计算数据的工作量也就越大,因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小。作业
P108 习题30.2 .2 2、3题课时作业设计
吸烟危害健康,这是不争的事实,请同学们做一调查,以估计你所在地区吸烟的人数。在做调查时,选取样本要注意有代表性,应注意各种人群不可遗漏,样本容量必须足够大,同时做好数据的搜集、整理工作。
成绩和标准差分别如下:样本平均成绩为78分,标准差为10.1分 图30.2.2另外,同学们也分别选取了一些样本,
它们同样也包含五个个体,如下表:同样,也可以作出这两个样本的频数分布直方图、计算它们的平均成绩和标准差,如下图所示: 样本平均成绩为80.8分,
标准差为6.5分样本平均成绩为
74.2分,
标准差为3.8分 5名学生成绩频数分布直方图第二样本第三样本5名学生成绩频数分布直方图图30.2.3 从以上三张图比较来看,它们之间存在
明显的差异,平均数和标准差与总体的平均
数与标准差也相去甚远,显然这样选择的样
本不能反映总体的特性,是不可靠的。样本平均成绩为79.7分,标准差为9.4分 让我们再用大一些的样本试一试,这次每个样本含有10个个体。图30.2.410名学生成绩频数分布直方图第二样本样本平均成绩为83.3分,标准差为11.5分 图30.2.4 我们继续用随机抽样方法,得到第一个样本,重复上述步骤,再取第二个样本。图30.2.4是根据小明取到的样本数据得到的频数分布直方图。 再选取一些含有10名学生的样本,我们发现此时不同样本的平均成绩和标准差似乎比较接近总体的平均成绩78.1分和标准差10.8分。看来用大一些的样本来估计总体会比较可靠一点,让我们再用更大一些的样本试一试,这次每个样本含有40个个体。图30.2.5是根据小明取到的两个样本数据得到的频数分布直方图。样本平均成绩为75.5分,标准差为10.2分 图30.2.540名学生成绩频数分布直方图第二样本样本平均成绩为77.1分,标准差为10.7分 图30.2.5 再选取一些含有40名学生的样本,我们发现此时不同样本的平均成绩和标准差与总体的平均成绩和标准差的差距更小了!(相当接近总体的平均成绩78.1)你们从自己的抽样过程中是否也得出了同样的结果?选择恰当的样本个体数目样本平均成绩为
75.7分,
标准差为10.2分 样本平均成绩为
77.1分,
标准差为10.7分火星岩石样本 当样本中个体太少时,样本的平均数、标准差往往差距较大,如果选取适当的样本的个体数,各个样本的平均数、标准差与总体的标准差相当接近。 三、课堂练习 请同学们在300名学生的成绩中用随机抽样的方法选取两个含有20个个体的样本,并计算出它们的平均数与标准差,绘制频数分布直方图,并与总体的平均数、标准差比较。 为了检查一批手榴弹的杀伤半径,抽取了其中20颗做试验,得到这20颗手榴弹的杀伤半径,并列表如下:练习:(1)在这个问题中,总体、个体、样本和样本容量各是什么?
(2)求出这20颗手榴弹的杀伤半径的众数、中位数和平均数,并估计这批手榴弹的平均杀伤半径.
解:
(1)总体是要检查的这批手榴弹的杀伤半径的全体;个体是每一颗手榴弹的杀伤半径;样本是所抽取的20颗手榴弹的杀伤半径;样本容量是20.
(2)在20个数据中,10出现了6次,次数最多,所以众数是10(米).
20个数据从小到大排列,第10个和第11个数据是最中间的两个数,分别为9(米)和10(米),所以中位数是9.5 (米).样本平均数9.4(米)小结
一般来说,用样本估计总体时,样本容量越大,样本对总体的估计也就越精确,相应地,搜集、整理、计算数据的工作量也就越大,因此,在实际工作中,样本容量既要考虑问题本身的需要,又要考虑实现的可能性和所付出的代价的大小。作业
P108 习题30.2 .2 2、3题课时作业设计
吸烟危害健康,这是不争的事实,请同学们做一调查,以估计你所在地区吸烟的人数。在做调查时,选取样本要注意有代表性,应注意各种人群不可遗漏,样本容量必须足够大,同时做好数据的搜集、整理工作。
