直角三角形的判定
图片预览



文档简介
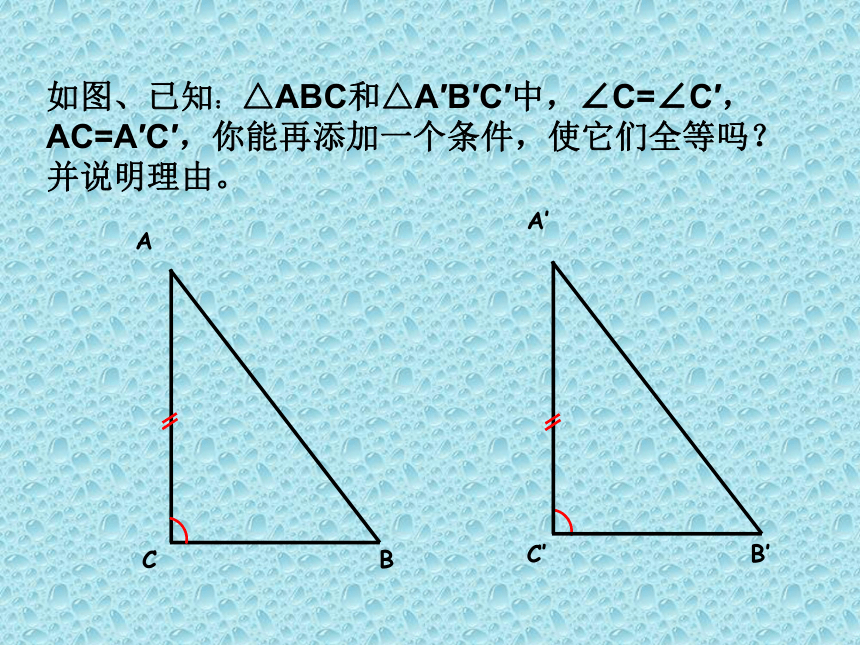
课件16张PPT。如图、已知: △ABC和△A′B′C′中,∠C=∠C′,AC=A′C′,你能再添加一个条件,使它们全等吗?并说明理由。ABCA′B′C′假设:∠C=∠C′=90°,AC=A′C′,添加
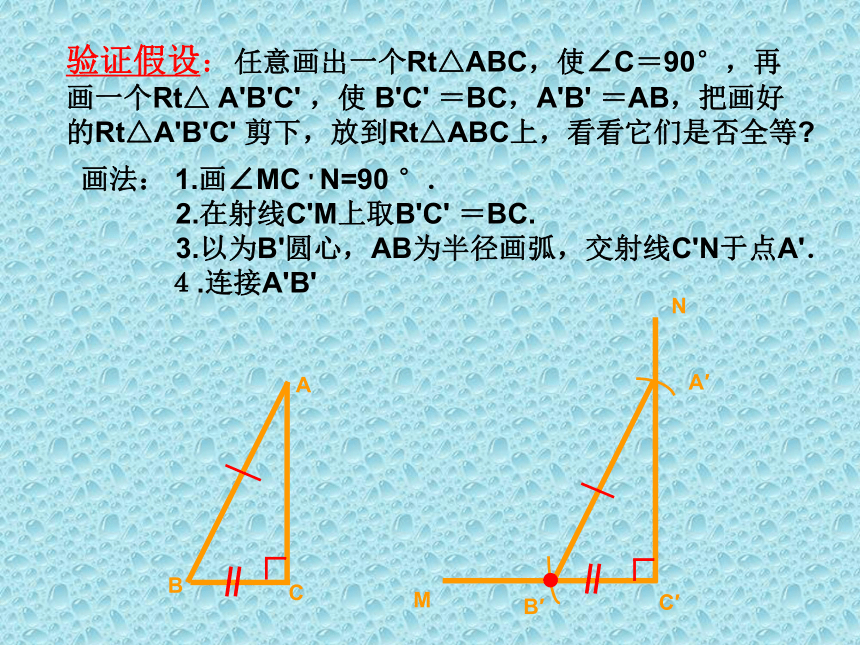
条件AB=A′B′,能使这两个直角三角形全等吗?ABCA′B′C′验证假设:任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,把画好的Rt△A'B'C' 剪下,放到Rt△ABC上,看看它们是否全等?画法: 1.画∠MC ' N=90 °.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
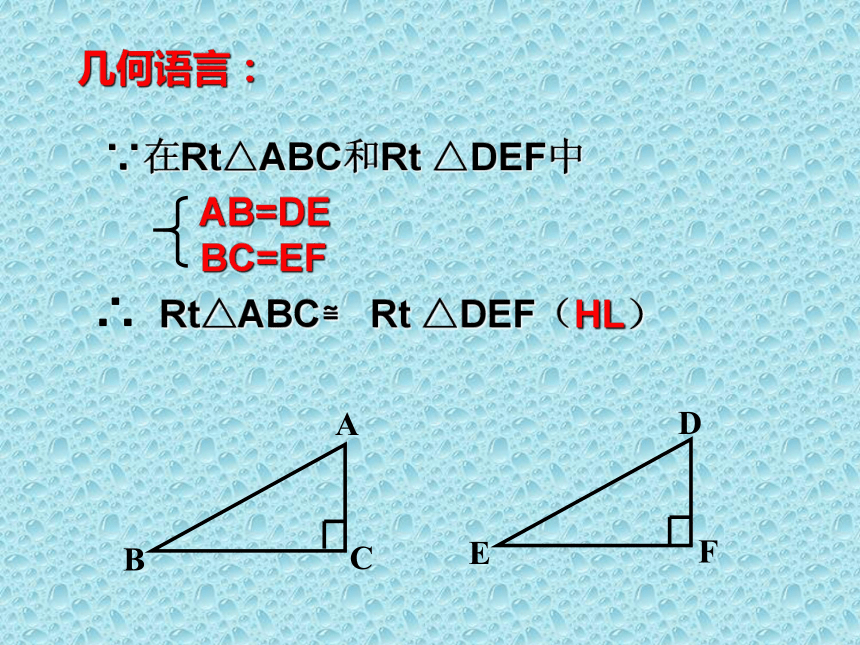
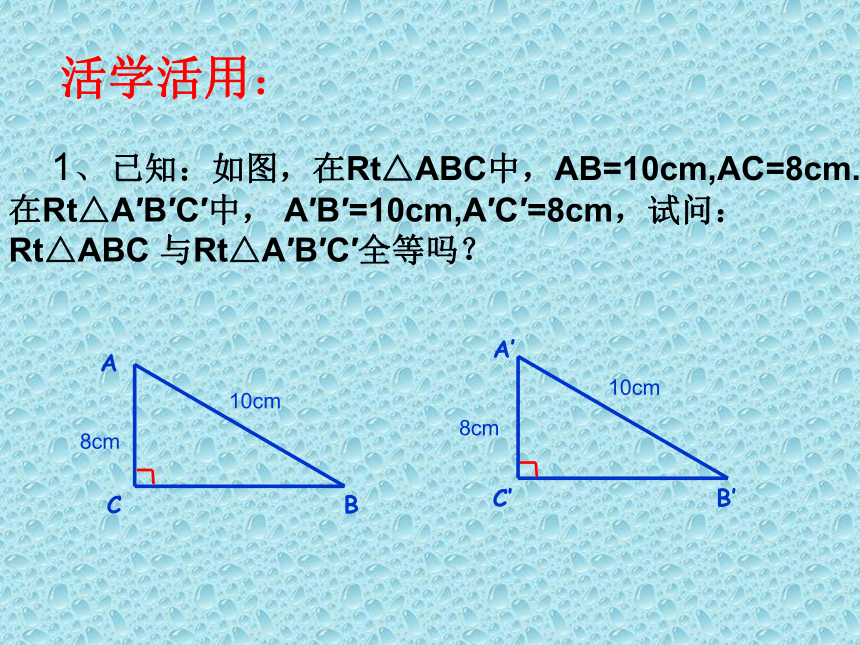
4.连接A'B' A′B′探索发现的规律是:验证假设提出假设行成规律探究性学习:几何语言:∵在Rt△ABC和Rt △DEF中 1、已知:如图,在Rt△ABC中,AB=10cm,AC=8cm.在Rt△A′B′C′中, A′B′=10cm,A′C′=8cm,试问: Rt△ABC 与Rt△A′B′C′全等吗?10cm10cm8cm8cm活学活用: 2、如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )
ASASASAAS×3、如图、∠ACB=∠ADB=90°,要使△ABC≌△BAD,还需添加一个什么条件?把添加的条件填在横线上,并在后面的括号中填上判定全等的理由。1
2
3
4
1、如图,AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
2、如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D、E 两地。DA⊥AB,EB⊥AB. D、E与路段AB的距离相等吗?为什么?
3、如图,已知:CE⊥AB,DF⊥AB, AC=BD,AF=BE, 求证:CE=DF。 反思小结:谈谈你在这节课的收获.作业:
教材P104 7 、 8祝同学们学习进步,天天向上!请各位同仁提出宝贵意见谢谢
条件AB=A′B′,能使这两个直角三角形全等吗?ABCA′B′C′验证假设:任意画出一个Rt△ABC,使∠C=90°,再画一个Rt△ A'B'C' ,使 B'C' =BC,A'B' =AB,把画好的Rt△A'B'C' 剪下,放到Rt△ABC上,看看它们是否全等?画法: 1.画∠MC ' N=90 °.
2.在射线C'M上取B'C' =BC.
3.以为B'圆心,AB为半径画弧,交射线C'N于点A'.
4.连接A'B' A′B′探索发现的规律是:验证假设提出假设行成规律探究性学习:几何语言:∵在Rt△ABC和Rt △DEF中 1、已知:如图,在Rt△ABC中,AB=10cm,AC=8cm.在Rt△A′B′C′中, A′B′=10cm,A′C′=8cm,试问: Rt△ABC 与Rt△A′B′C′全等吗?10cm10cm8cm8cm活学活用: 2、如图,具有下列条件的Rt△ABC与Rt△DEF(其中∠C=∠F=90°)是否全等,在( )里填写理由;如果不全等,在( )里打“×”:
(1)AC=DF,∠A=∠D ( )
(2)AC=DF,BC=EF ( )
(3)AB=DE,∠B=∠E ( )
(4)∠A=∠D,∠B=∠E ( )
ASASASAAS×3、如图、∠ACB=∠ADB=90°,要使△ABC≌△BAD,还需添加一个什么条件?把添加的条件填在横线上,并在后面的括号中填上判定全等的理由。1
2
3
4
1、如图,AC⊥BC,BD⊥AD,AC=BD.
求证:BC=AD.
2、如图,C是路段AB的中点,两人从C同时出发,以相同的速度分别沿着两条直线行走,并同时到达D、E 两地。DA⊥AB,EB⊥AB. D、E与路段AB的距离相等吗?为什么?
3、如图,已知:CE⊥AB,DF⊥AB, AC=BD,AF=BE, 求证:CE=DF。 反思小结:谈谈你在这节课的收获.作业:
教材P104 7 、 8祝同学们学习进步,天天向上!请各位同仁提出宝贵意见谢谢
