24.1 圆的有关性质综合检测题(含解析)
文档属性
| 名称 | 24.1 圆的有关性质综合检测题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 726.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 07:45:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.1 圆的有关性质综合检测题
一、填空题
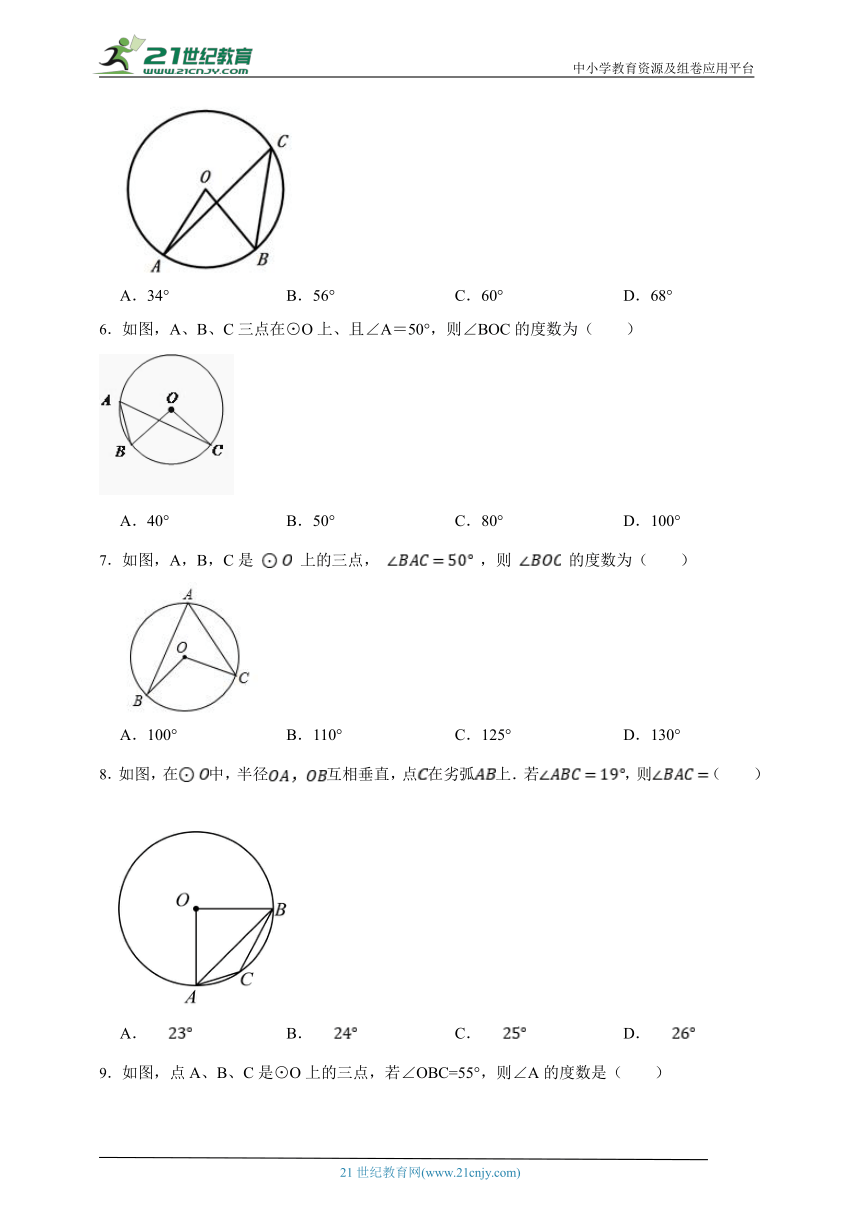
1.如图,已知AB,CD是☉O的直径,弧AE=弧AC,∠AOE=32°,那么∠COE的度数为 度.
2.如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=50°,则∠ACB= °.
3.如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为 度.
二、单选题
4.如图,∠A是⊙O的圆周角,∠A=40°,则∠BOC=( )
A.30° B.40° C.80° D.60°
5.如图,点 , , 都在 上,若 ,则 为( )
A.34° B.56° C.60° D.68°
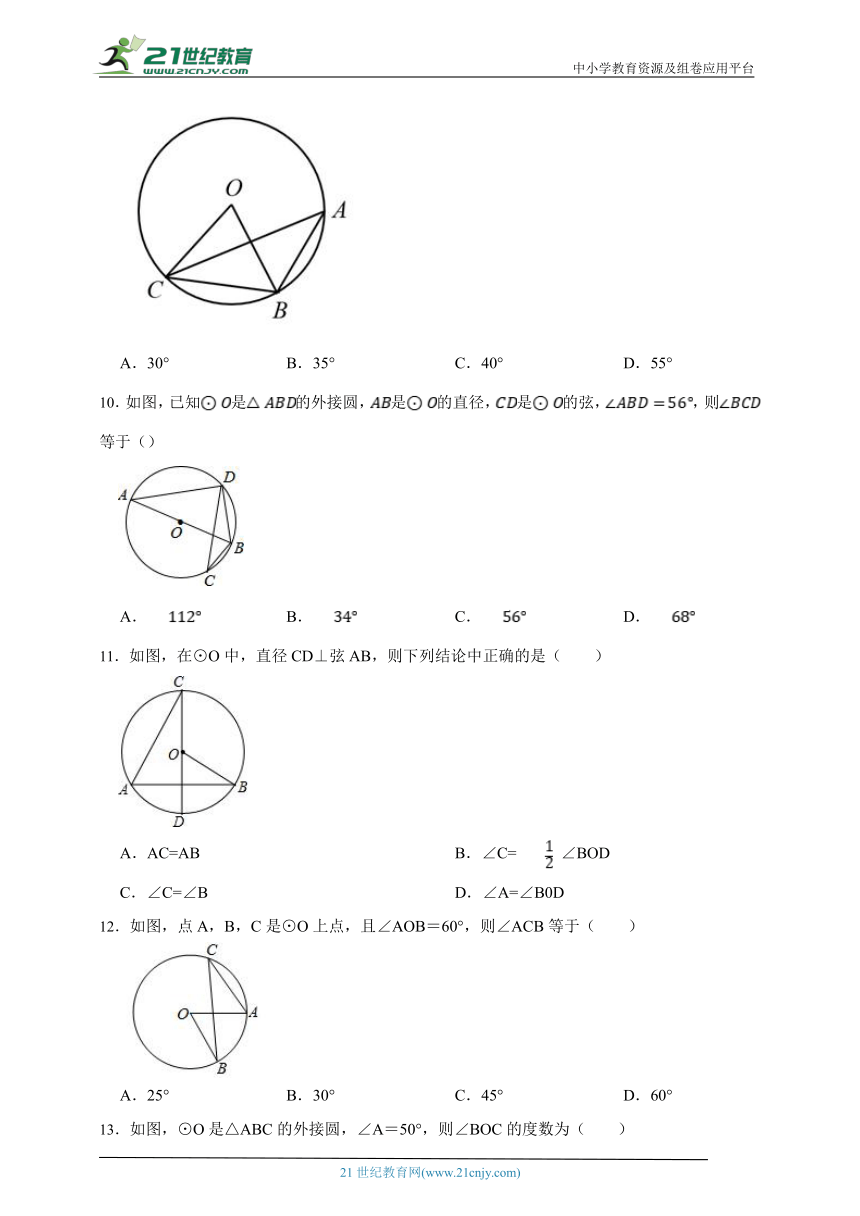
6.如图,A、B、C三点在⊙O上、且∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.80° D.100°
7.如图,A,B,C是 上的三点, ,则 的度数为( )
A.100° B.110° C.125° D.130°
8.如图,在中,半径互相垂直,点在劣弧上.若,则( )
A. B. C. D.
9.如图,点A、B、C是⊙O上的三点,若∠OBC=55°,则∠A的度数是( )
A.30° B.35° C.40° D.55°
10.如图,已知是的外接圆,是的直径,是的弦,,则等于()
A. B. C. D.
11.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C= ∠BOD
C.∠C=∠B D.∠A=∠B0D
12.如图,点A,B,C是⊙O上点,且∠AOB=60°,则∠ACB等于( )
A.25° B.30° C.45° D.60°
13.如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.80° D.100°
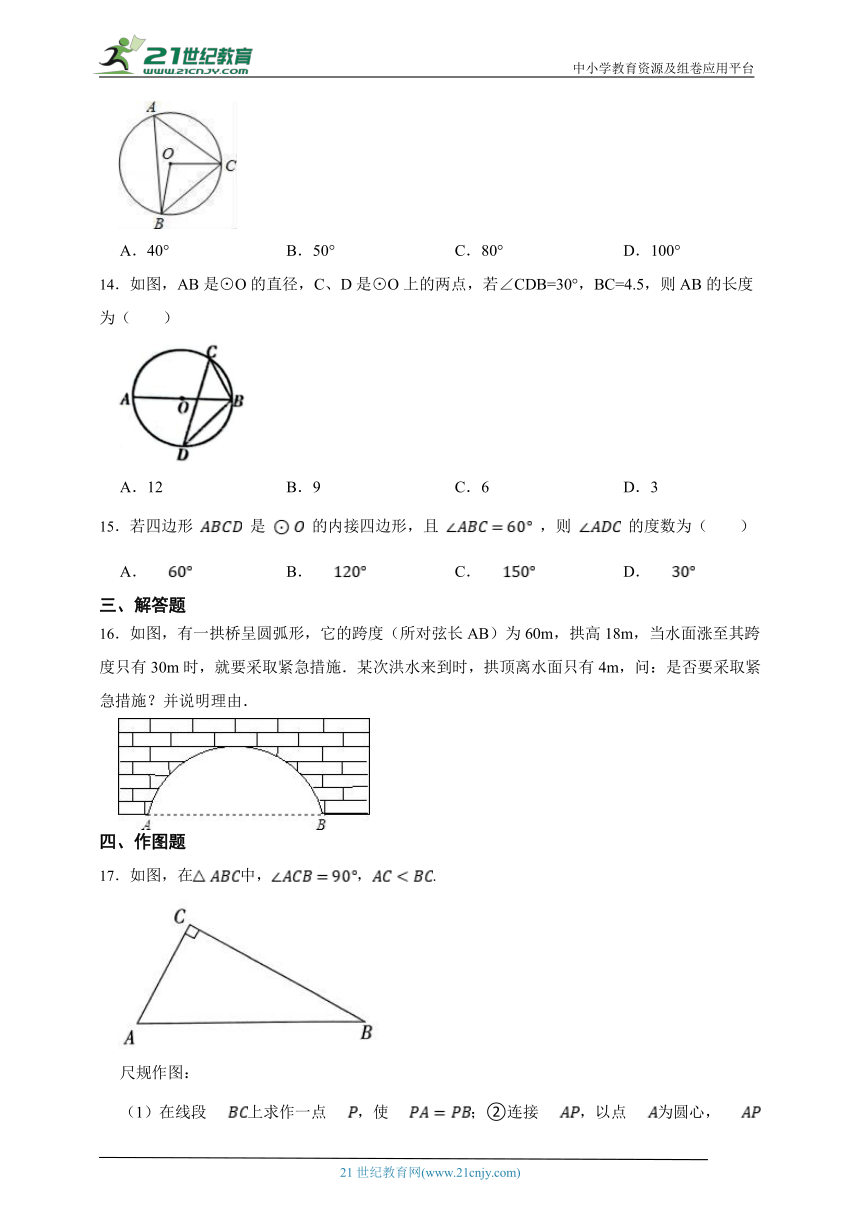
14.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CDB=30°,BC=4.5,则AB的长度为( )
A.12 B.9 C.6 D.3
15.若四边形 是 的内接四边形,且 ,则 的度数为( )
A. B. C. D.
三、解答题
16.如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.
四、作图题
17.如图,在中,,.
尺规作图:
(1)在线段上求作一点,使;②连接,以点为圆心,的长为半径画弧,交的延长线于点,连接.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,求的度数;
(3)在(1)的条件下,若,求的周长.
18.如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的圆心吗?(保留作图痕迹)
五、综合题
19.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
20.如图,AB为 的直径,CD是弦,且 于点E,连接AC、OC、BC.
(1)求证: .
(2)若 , ,求 的直径.
答案解析部分
1.【答案】64
【解析】【解答】解:∵ ,(已知)
∴∠AOE=∠COA(等弧所对的圆心角相等);
又∠AOE=32°,
∴∠COA=32°,
∴∠COE=∠AOE+∠COA=64°。
故答案是:64°。
【分析】根据等弧所对的圆心角相等得出∠AOE=∠COA=32°,进而根据∠COE=∠AOE+∠COA算出答案。
2.【答案】40
【解析】【解答】解:连接BD,如图,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∴∠D=90°﹣∠BAD=90°﹣50°=40°,
∴∠ACB=∠D=40°.
故答案为40.
【分析】连接BD,如图,根据直径所对的圆周角是直角得出∠ABD=90°,根据三角形的内角和得出∠D,根据同弧所对的圆周角相等得出∠ACB的度数。
3.【答案】30
【解析】【解答】解:连接OC,∵弦CD垂直平分半径OA,
∴OE=
OC,
∴∠OCD=30°,∠AOC=60°,
∴∠ABC=30°.
故答案为:30.
【分析】根据线段的特殊关系求角的大小,再运用圆周角定理求解.
4.【答案】C
【解析】【解答】解:∵∠A是⊙O的圆周角,∠A=40°,
∴∠BOC=2∠A=80°.
故答案为:C.
【分析】利用圆周角的性质可得∠BOC=2∠A=80°。
5.【答案】D
【解析】【解答】解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故答案为:D.
【分析】由同弧所对得圆心角是圆周角的2倍, 可得答案.
6.【答案】D
【解析】【分析】在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,由此可得∠BOC=2∠A=100°.
故选D.
7.【答案】A
【解析】【解答】解: 所对的圆心角为 ,所对的圆周角为 , ,
,
故答案为: .
【分析】根据圆周角的性质:同弧所对的圆周角等于圆心角的一半求解即可。
8.【答案】D
【解析】【解答】解:如图,连接OC,
∵∠ABC=19°,
∴∠AOC=2∠ABC=38°,
∵∠AOB=90°,
∴∠BOC=∠AOB-∠AOC=52°,
∴∠BAC=∠BOC=26°.
故答案为:D.
【分析】连接OC,由同弧所对的圆心角等于圆周角的2倍得∠AOC=2∠ABC=38°,由角的和差可得∠BOC=52°,进而再由同弧所对的圆周角等于圆心角的一半求出∠BAC的度数.
9.【答案】B
【解析】【解答】解:根据题意,
∵OB=OC,
∴∠OCB=∠OBC=55°,
∴∠BOC=180° 55° 55°=70°,
∴ ;
故答案为:B.
【分析】由等边对等角和三角形的内角和定理,先求出∠BOC=70°,再由同弧所对的圆心角等于圆周角的2倍,即可求出答案.
10.【答案】B
【解析】【解答】解:∵ 是 的直径,
∴ ,
∴ ,
∴ ,
故答案为:B.
【分析】根据直径所对的圆周角是直角得∠ADB=90°,根据直角三角形的两锐角互余得∠A=34°,进而根据同弧所对的圆周角相等即可得出∠BCD=∠A,从而即可得出答案.
11.【答案】B
【解析】【解答】解:∵直径CD⊥弦AB,
∴弧AD =弧BD,
∴∠C= ∠BOD.
故答案为:B.
【分析】先利用垂径定理得到弧AD=弧BD,然后根据圆周角定理得到∠C= ∠BOD,从而可对各选项进行判断.
12.【答案】B
【解析】【解答】解:∵点A,B,C是⊙O上点,且∠AOB=60°,
∴∠ACB= ∠AOB=30°,
故答案为:B.
【分析】根据题意求出∠ACB= ∠AOB=30°,即可作答。
13.【答案】D
【解析】【解答】解:∵⊙O是△ABC的外接圆,∠A=50°,
∴∠BOC=2∠A=100°.
故答案为:D.
【分析】由⊙O是△ABC的外接圆,∠A=50°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BOC的度数.
14.【答案】B
【解析】【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=30°,
∴AB=2BC=2×4.5=9.
故答案为:B.
【分析】连接AC,根据圆周角定理得出∠ACB=90°,∠A=∠CDB=30°,再根据直角三角形30°角所对的边等于斜边的一半得出AB=2BC,即可得出答案.
15.【答案】B
【解析】【解答】解:∵四边形ABCD是⊙O的内接四边形,∠ABC=60°,
∴∠ADC=180° ∠ABC=180° 60°=120°,
故答案为:B.
【分析】根据圆内接四边形的对角线互补计算得到答案。
16.【答案】解:连接OA′,OA.
设圆的半径是R米,则ON=(R﹣4)米,OM=(R﹣18)米.
根据垂径定理,得AM= AB=30米,
在Rt△AOM中,AO2=OM2+AM2,
即R2=(R﹣18)2+900,
解得:R=34.
在Rt△A′ON中,根据勾股定理得A′N= =16米,
根据垂径定理,得:A′B′=2A′N=32>30.
∴不用采取紧急措施.
【解析】【分析】连接OA′,OA.设圆的半径是R,则ON=R﹣4,OM=R﹣18.根据垂径定理求得AM的长,在Rt△AOM中,根据勾股定理求得R的值,在Rt△A′ON中,根据勾股定理求得A′N的值,再根据垂径定理求得A′B′的长,从而作出判断.
17.【答案】(1)解:如图所示
(2)解:∵,
∴
∵在中,
∴
(3)解:∵,∴
∵由作图可知,
即
∴
∴的周长为
【解析】【分析】(1)根据题意作图即可。
(2)因为PA=PB,所以∠PAB=∠PBA,这里利用了两边相等,则该三角形为等边三角形,等腰三角形两底角相等,又因为三角形的一个外角等于与它不相邻的两个内角之和,所以可以得出∠PAC=∠PAB+∠ABP=25°+25°,又∠ACB=90°,根据三角形的内角和为180°,所以∠CAB=180°-∠ACB-∠PAC=180°-90°-25°-25°=40°,故得出∠PAC=40°。
(3)因为BC=8,根据题中所给PA=PB,可以得到AP+PC=BC,因为AP,AQ都为圆的半径,一个圆的半径都相等,即可得到AQ=AP,又有AC⊥PQ,根据垂线上的点到线段两边的距离相等可以得出AC为PQ垂直平分线,所以可得CP=CQ,所以可以得到AQ+CQ=AP+PC,前面中我们得到AP+PC=BC,的周长=2(AP+CP)=2BC,故可得的周长为2BC.
18.【答案】解:如图所示:
点O即为车轮的圆心.
【解析】【分析】作圆的两条弦CD,DE,再作出弦CD,DE的垂直平分线,它们的交点就是圆心,即可求解.
19.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【解析】【分析】(1)直接利用直角三角形中30°所对的边等于斜边的一半求出即可;(2)根据题意可知,图中AB=50m,AD⊥BC,且BD=CD,∠AOD=30°,OA=80m;再利用垂径定理及勾股定理解答即可.
20.【答案】(1)证明:∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴
(2)解:设 的半径为 ,
∴ , ,
∵ ,
∴ ,
在 中, ,
即, ,
解得, ,
所以直径为 .
【解析】【分析】(1)先根据圆周角定理得到
,再由等腰三角形性质得到∠OAC=∠ACO,进而得到
.
(2) 设 的半径为 ,由垂径定理得到
,再根据勾股定理得到
,求出r,进而求出直径.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.1 圆的有关性质综合检测题
一、填空题
1.如图,已知AB,CD是☉O的直径,弧AE=弧AC,∠AOE=32°,那么∠COE的度数为 度.
2.如图,AD为△ABC的外接圆⊙O的直径,若∠BAD=50°,则∠ACB= °.
3.如图,AB是⊙O的直径,弦CD垂直平分半径OA,则∠ABC的大小为 度.
二、单选题
4.如图,∠A是⊙O的圆周角,∠A=40°,则∠BOC=( )
A.30° B.40° C.80° D.60°
5.如图,点 , , 都在 上,若 ,则 为( )
A.34° B.56° C.60° D.68°
6.如图,A、B、C三点在⊙O上、且∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.80° D.100°
7.如图,A,B,C是 上的三点, ,则 的度数为( )
A.100° B.110° C.125° D.130°
8.如图,在中,半径互相垂直,点在劣弧上.若,则( )
A. B. C. D.
9.如图,点A、B、C是⊙O上的三点,若∠OBC=55°,则∠A的度数是( )
A.30° B.35° C.40° D.55°
10.如图,已知是的外接圆,是的直径,是的弦,,则等于()
A. B. C. D.
11.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C= ∠BOD
C.∠C=∠B D.∠A=∠B0D
12.如图,点A,B,C是⊙O上点,且∠AOB=60°,则∠ACB等于( )
A.25° B.30° C.45° D.60°
13.如图,⊙O是△ABC的外接圆,∠A=50°,则∠BOC的度数为( )
A.40° B.50° C.80° D.100°
14.如图,AB是⊙O的直径,C、D是⊙O上的两点,若∠CDB=30°,BC=4.5,则AB的长度为( )
A.12 B.9 C.6 D.3
15.若四边形 是 的内接四边形,且 ,则 的度数为( )
A. B. C. D.
三、解答题
16.如图,有一拱桥呈圆弧形,它的跨度(所对弦长AB)为60m,拱高18m,当水面涨至其跨度只有30m时,就要采取紧急措施.某次洪水来到时,拱顶离水面只有4m,问:是否要采取紧急措施?并说明理由.
四、作图题
17.如图,在中,,.
尺规作图:
(1)在线段上求作一点,使;②连接,以点为圆心,的长为半径画弧,交的延长线于点,连接.(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,求的度数;
(3)在(1)的条件下,若,求的周长.
18.如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的圆心吗?(保留作图痕迹)
五、综合题
19.如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
(1)求对学校A的噪声影响最大时卡车P与学校A的距离;
(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.
20.如图,AB为 的直径,CD是弦,且 于点E,连接AC、OC、BC.
(1)求证: .
(2)若 , ,求 的直径.
答案解析部分
1.【答案】64
【解析】【解答】解:∵ ,(已知)
∴∠AOE=∠COA(等弧所对的圆心角相等);
又∠AOE=32°,
∴∠COA=32°,
∴∠COE=∠AOE+∠COA=64°。
故答案是:64°。
【分析】根据等弧所对的圆心角相等得出∠AOE=∠COA=32°,进而根据∠COE=∠AOE+∠COA算出答案。
2.【答案】40
【解析】【解答】解:连接BD,如图,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∴∠D=90°﹣∠BAD=90°﹣50°=40°,
∴∠ACB=∠D=40°.
故答案为40.
【分析】连接BD,如图,根据直径所对的圆周角是直角得出∠ABD=90°,根据三角形的内角和得出∠D,根据同弧所对的圆周角相等得出∠ACB的度数。
3.【答案】30
【解析】【解答】解:连接OC,∵弦CD垂直平分半径OA,
∴OE=
OC,
∴∠OCD=30°,∠AOC=60°,
∴∠ABC=30°.
故答案为:30.
【分析】根据线段的特殊关系求角的大小,再运用圆周角定理求解.
4.【答案】C
【解析】【解答】解:∵∠A是⊙O的圆周角,∠A=40°,
∴∠BOC=2∠A=80°.
故答案为:C.
【分析】利用圆周角的性质可得∠BOC=2∠A=80°。
5.【答案】D
【解析】【解答】解:∵∠C=34°,
∴∠AOB=2∠C=68°.
故答案为:D.
【分析】由同弧所对得圆心角是圆周角的2倍, 可得答案.
6.【答案】D
【解析】【分析】在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,由此可得∠BOC=2∠A=100°.
故选D.
7.【答案】A
【解析】【解答】解: 所对的圆心角为 ,所对的圆周角为 , ,
,
故答案为: .
【分析】根据圆周角的性质:同弧所对的圆周角等于圆心角的一半求解即可。
8.【答案】D
【解析】【解答】解:如图,连接OC,
∵∠ABC=19°,
∴∠AOC=2∠ABC=38°,
∵∠AOB=90°,
∴∠BOC=∠AOB-∠AOC=52°,
∴∠BAC=∠BOC=26°.
故答案为:D.
【分析】连接OC,由同弧所对的圆心角等于圆周角的2倍得∠AOC=2∠ABC=38°,由角的和差可得∠BOC=52°,进而再由同弧所对的圆周角等于圆心角的一半求出∠BAC的度数.
9.【答案】B
【解析】【解答】解:根据题意,
∵OB=OC,
∴∠OCB=∠OBC=55°,
∴∠BOC=180° 55° 55°=70°,
∴ ;
故答案为:B.
【分析】由等边对等角和三角形的内角和定理,先求出∠BOC=70°,再由同弧所对的圆心角等于圆周角的2倍,即可求出答案.
10.【答案】B
【解析】【解答】解:∵ 是 的直径,
∴ ,
∴ ,
∴ ,
故答案为:B.
【分析】根据直径所对的圆周角是直角得∠ADB=90°,根据直角三角形的两锐角互余得∠A=34°,进而根据同弧所对的圆周角相等即可得出∠BCD=∠A,从而即可得出答案.
11.【答案】B
【解析】【解答】解:∵直径CD⊥弦AB,
∴弧AD =弧BD,
∴∠C= ∠BOD.
故答案为:B.
【分析】先利用垂径定理得到弧AD=弧BD,然后根据圆周角定理得到∠C= ∠BOD,从而可对各选项进行判断.
12.【答案】B
【解析】【解答】解:∵点A,B,C是⊙O上点,且∠AOB=60°,
∴∠ACB= ∠AOB=30°,
故答案为:B.
【分析】根据题意求出∠ACB= ∠AOB=30°,即可作答。
13.【答案】D
【解析】【解答】解:∵⊙O是△ABC的外接圆,∠A=50°,
∴∠BOC=2∠A=100°.
故答案为:D.
【分析】由⊙O是△ABC的外接圆,∠A=50°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠BOC的度数.
14.【答案】B
【解析】【解答】解:连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=∠CDB=30°,
∴AB=2BC=2×4.5=9.
故答案为:B.
【分析】连接AC,根据圆周角定理得出∠ACB=90°,∠A=∠CDB=30°,再根据直角三角形30°角所对的边等于斜边的一半得出AB=2BC,即可得出答案.
15.【答案】B
【解析】【解答】解:∵四边形ABCD是⊙O的内接四边形,∠ABC=60°,
∴∠ADC=180° ∠ABC=180° 60°=120°,
故答案为:B.
【分析】根据圆内接四边形的对角线互补计算得到答案。
16.【答案】解:连接OA′,OA.
设圆的半径是R米,则ON=(R﹣4)米,OM=(R﹣18)米.
根据垂径定理,得AM= AB=30米,
在Rt△AOM中,AO2=OM2+AM2,
即R2=(R﹣18)2+900,
解得:R=34.
在Rt△A′ON中,根据勾股定理得A′N= =16米,
根据垂径定理,得:A′B′=2A′N=32>30.
∴不用采取紧急措施.
【解析】【分析】连接OA′,OA.设圆的半径是R,则ON=R﹣4,OM=R﹣18.根据垂径定理求得AM的长,在Rt△AOM中,根据勾股定理求得R的值,在Rt△A′ON中,根据勾股定理求得A′N的值,再根据垂径定理求得A′B′的长,从而作出判断.
17.【答案】(1)解:如图所示
(2)解:∵,
∴
∵在中,
∴
(3)解:∵,∴
∵由作图可知,
即
∴
∴的周长为
【解析】【分析】(1)根据题意作图即可。
(2)因为PA=PB,所以∠PAB=∠PBA,这里利用了两边相等,则该三角形为等边三角形,等腰三角形两底角相等,又因为三角形的一个外角等于与它不相邻的两个内角之和,所以可以得出∠PAC=∠PAB+∠ABP=25°+25°,又∠ACB=90°,根据三角形的内角和为180°,所以∠CAB=180°-∠ACB-∠PAC=180°-90°-25°-25°=40°,故得出∠PAC=40°。
(3)因为BC=8,根据题中所给PA=PB,可以得到AP+PC=BC,因为AP,AQ都为圆的半径,一个圆的半径都相等,即可得到AQ=AP,又有AC⊥PQ,根据垂线上的点到线段两边的距离相等可以得出AC为PQ垂直平分线,所以可得CP=CQ,所以可以得到AQ+CQ=AP+PC,前面中我们得到AP+PC=BC,的周长=2(AP+CP)=2BC,故可得的周长为2BC.
18.【答案】解:如图所示:
点O即为车轮的圆心.
【解析】【分析】作圆的两条弦CD,DE,再作出弦CD,DE的垂直平分线,它们的交点就是圆心,即可求解.
19.【答案】(1)解:过点A作AD⊥ON于点D,
∵∠NOM=30°,AO=80m,
∴AD=40m,
即对学校A的噪声影响最大时卡车P与学校A的距离为40米;
(2)解:由图可知:以50m为半径画圆,分别交ON于B,C两点,AD⊥BC,BD=CD= BC,OA=80m,
∵在Rt△AOD中,∠AOB=30°,
∴AD= OA= ×80=40m,
在Rt△ABD中,AB=50,AD=40,由勾股定理得:BD= = =30m,
故BC=2×30=60米,即重型运输卡车在经过BC时对学校产生影响.
∵重型运输卡车的速度为18千米/小时,即 =300米/分钟,
∴重型运输卡车经过BC时需要60÷300=0.2(分钟)=12(秒).
答:卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间为12秒
【解析】【分析】(1)直接利用直角三角形中30°所对的边等于斜边的一半求出即可;(2)根据题意可知,图中AB=50m,AD⊥BC,且BD=CD,∠AOD=30°,OA=80m;再利用垂径定理及勾股定理解答即可.
20.【答案】(1)证明:∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∴
(2)解:设 的半径为 ,
∴ , ,
∵ ,
∴ ,
在 中, ,
即, ,
解得, ,
所以直径为 .
【解析】【分析】(1)先根据圆周角定理得到
,再由等腰三角形性质得到∠OAC=∠ACO,进而得到
.
(2) 设 的半径为 ,由垂径定理得到
,再根据勾股定理得到
,求出r,进而求出直径.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
