24.3 正多边形和圆一课一练(含解析)
文档属性
| 名称 | 24.3 正多边形和圆一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 629.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
24.3 正多边形和圆一课一练
一、填空题
1.已知四边形内接于,若,则的度数为 .
2.一个正方形和两个等边三角形的位置如图所示,则∠1+∠2+∠3 的度数为 .
二、单选题
3.如果一个多边形的每个内角都是120°,那么这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )
A.140° B.70° C.80° D.60°
5.如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A.15° B.30° C.45° D.60°
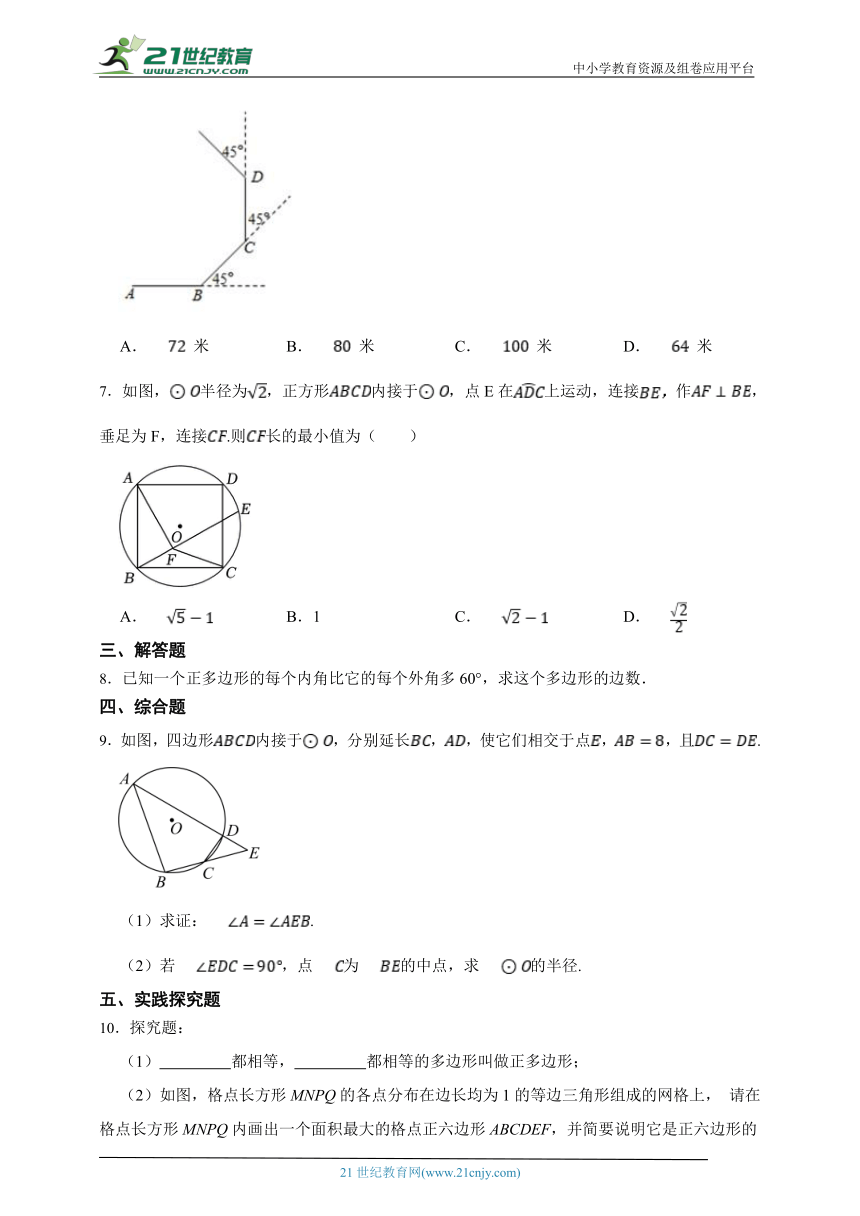
6.如图,小明从点A出发沿直线前进 米到达点B,向左转 后又沿直线前进 米到达点C,再向左转 后沿直线前进 米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A. 米 B. 米 C. 米 D. 米
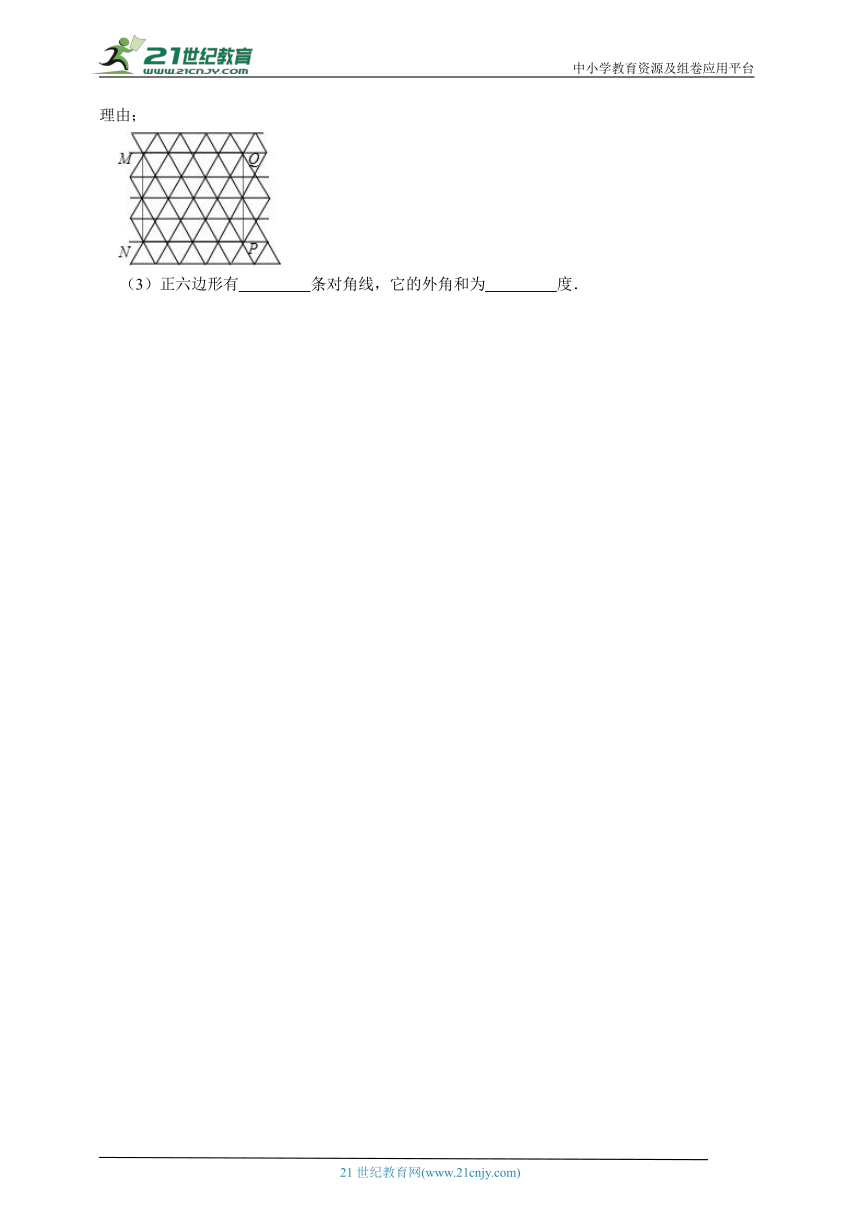
7.如图,半径为,正方形内接于,点E在上运动,连接作,垂足为F,连接.则长的最小值为( )
A. B.1 C. D.
三、解答题
8.已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
四、综合题
9.如图,四边形内接于,分别延长,,使它们相交于点,,且.
(1)求证:.
(2)若,点为的中点,求的半径.
五、实践探究题
10.探究题:
(1) 都相等, 都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上, 请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有 条对角线,它的外角和为 度.
答案解析部分
1.【答案】50°
【解析】【解答】解:∵四边形 内接于 ,
∴ ,
∵ ,
∴ ,
故答案为:50°.
【分析】根据圆内接四边形对角互补可得∠A+∠C=180°,据此计算.
2.【答案】150°
【解析】【解答】如图,
在△ABC中,
∴
∴
故答案为:
【分析】根据等边三角形的性质及正方形的性质,由平角的定义即可分别表示出∠BAC,∠ABC,∠ACB,又根据三角形的内角和知∠BAC+∠ABC+∠ACB =180 , 从而建立方程即可得出答案。
3.【答案】B
【解析】【解答】一个多边形的每个内角都是120°,可知每一个外角为60°,所以这个多边形的边数为=6。
故答案为:B.
【分析】多边形的外角和是360°.
4.【答案】A
【解析】【解答】∵四边形ABCD是圆内接四边形
∴∠A+∠C=180°,
∵∠C=110°,
∴∠A=180°﹣∠C=70°,
由圆周角定理得,∠BOD=2∠A=140°,
故答案为:A.
【分析】根据圆内接四边形的对角互补求出∠A的度数,根据圆周角定理得到答案.
5.【答案】B
【解析】【解答】解:连接OA、OB、如图所示:
∵∠AOB= =60°,
∴∠APC= ∠AOC=30°.
故答案为:B.
【分析】由正六边形的性质得出∠AOB=120°,由圆周角定理求出∠APC=30°.
6.【答案】A
【解析】【解答】解:∵小明每次都是沿直线前进9米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×9=72(m).
故答案为:A.
【分析】 根据题意,小明走过的路程是正多边形,且该正多边形每一个外角都等于45°,故用360°除以45°求出边数,然后再乘以10米即可求解.
7.【答案】A
【解析】【解答】解:如图,连接,取的中点K,连接,
∵,
∴,
∵,
∴,
∵正方形的外接圆的半径为,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴CF的最小值为.
故答案为:A.
【分析】连接,取的中点K,连接,由直角三角形斜边中线的性质及 半径为 ,可得KF=AK=BK=1,由勾股定理求出CK=,根据即可求解.
8.【答案】解:设内角为x°,则外角为(x﹣60)°,由题意得:
x+x﹣60=180,
解得:x=120,
则外角为120°﹣60°=60°,
多边形的边数:360°÷60°=6.
【解析】【分析】设内角为x°,则外角为(x﹣60)°,根据题意列出方程x+x﹣60=180,求出x的值,再利用多边形的边数=外角和÷一个外角的度数可得答案。
9.【答案】(1)证明:∵四边形内接于,
∴,
∵,
∴,
∵
∴,
∴
(2)解:如图,连接
∵,
∴是的直径,
∴,
∵
∴
∵,
∴,
∵点为的中点,
∴,
在中,,
∴的半径为
【解析】【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,由邻补角的性质可得∠BCD+∠DCE=180°,则∠A=∠DCE,由等腰三角形的性质可得∠E=∠DCE,据此证明;
(2)连接AC,则AC为直径,由圆周角定理可得∠ABC=90°,根据∠A=∠AEB可得AB=BE=8,由中点的概念可得BC的值,然后利用勾股定理进行计算即可.
10.【答案】(1)各个角;各条边
(2)解:如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24×=;
(3)9;360°
【解析】【解答】解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
【分析】(1)根据正多边形的定义求解即可;
(2)先求出 AB=BC=CD=DE=EF=FA, 再求出 六边形ABCDEFA是正六边形,最后求解即可;
(3)先求出正六边形的对角线条数为9,再求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.3 正多边形和圆一课一练
一、填空题
1.已知四边形内接于,若,则的度数为 .
2.一个正方形和两个等边三角形的位置如图所示,则∠1+∠2+∠3 的度数为 .
二、单选题
3.如果一个多边形的每个内角都是120°,那么这个多边形是( )
A.五边形 B.六边形 C.七边形 D.八边形
4.如图,在圆内接四边形ABCD中,∠C=110°,则∠BOD的度数为( )
A.140° B.70° C.80° D.60°
5.如图,正六边形ABCDEF内接于⊙O,点P是 上的任意一点,则∠APB的大小是( )
A.15° B.30° C.45° D.60°
6.如图,小明从点A出发沿直线前进 米到达点B,向左转 后又沿直线前进 米到达点C,再向左转 后沿直线前进 米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
A. 米 B. 米 C. 米 D. 米
7.如图,半径为,正方形内接于,点E在上运动,连接作,垂足为F,连接.则长的最小值为( )
A. B.1 C. D.
三、解答题
8.已知一个正多边形的每个内角比它的每个外角多60°,求这个多边形的边数.
四、综合题
9.如图,四边形内接于,分别延长,,使它们相交于点,,且.
(1)求证:.
(2)若,点为的中点,求的半径.
五、实践探究题
10.探究题:
(1) 都相等, 都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上, 请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有 条对角线,它的外角和为 度.
答案解析部分
1.【答案】50°
【解析】【解答】解:∵四边形 内接于 ,
∴ ,
∵ ,
∴ ,
故答案为:50°.
【分析】根据圆内接四边形对角互补可得∠A+∠C=180°,据此计算.
2.【答案】150°
【解析】【解答】如图,
在△ABC中,
∴
∴
故答案为:
【分析】根据等边三角形的性质及正方形的性质,由平角的定义即可分别表示出∠BAC,∠ABC,∠ACB,又根据三角形的内角和知∠BAC+∠ABC+∠ACB =180 , 从而建立方程即可得出答案。
3.【答案】B
【解析】【解答】一个多边形的每个内角都是120°,可知每一个外角为60°,所以这个多边形的边数为=6。
故答案为:B.
【分析】多边形的外角和是360°.
4.【答案】A
【解析】【解答】∵四边形ABCD是圆内接四边形
∴∠A+∠C=180°,
∵∠C=110°,
∴∠A=180°﹣∠C=70°,
由圆周角定理得,∠BOD=2∠A=140°,
故答案为:A.
【分析】根据圆内接四边形的对角互补求出∠A的度数,根据圆周角定理得到答案.
5.【答案】B
【解析】【解答】解:连接OA、OB、如图所示:
∵∠AOB= =60°,
∴∠APC= ∠AOC=30°.
故答案为:B.
【分析】由正六边形的性质得出∠AOB=120°,由圆周角定理求出∠APC=30°.
6.【答案】A
【解析】【解答】解:∵小明每次都是沿直线前进9米后向左转45度,
∴他走过的图形是正多边形,
∴边数n=360°÷45°=8,
∴他第一次回到出发点A时,一共走了8×9=72(m).
故答案为:A.
【分析】 根据题意,小明走过的路程是正多边形,且该正多边形每一个外角都等于45°,故用360°除以45°求出边数,然后再乘以10米即可求解.
7.【答案】A
【解析】【解答】解:如图,连接,取的中点K,连接,
∵,
∴,
∵,
∴,
∵正方形的外接圆的半径为,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∴CF的最小值为.
故答案为:A.
【分析】连接,取的中点K,连接,由直角三角形斜边中线的性质及 半径为 ,可得KF=AK=BK=1,由勾股定理求出CK=,根据即可求解.
8.【答案】解:设内角为x°,则外角为(x﹣60)°,由题意得:
x+x﹣60=180,
解得:x=120,
则外角为120°﹣60°=60°,
多边形的边数:360°÷60°=6.
【解析】【分析】设内角为x°,则外角为(x﹣60)°,根据题意列出方程x+x﹣60=180,求出x的值,再利用多边形的边数=外角和÷一个外角的度数可得答案。
9.【答案】(1)证明:∵四边形内接于,
∴,
∵,
∴,
∵
∴,
∴
(2)解:如图,连接
∵,
∴是的直径,
∴,
∵
∴
∵,
∴,
∵点为的中点,
∴,
在中,,
∴的半径为
【解析】【分析】(1)根据圆内接四边形的性质可得∠A+∠BCD=180°,由邻补角的性质可得∠BCD+∠DCE=180°,则∠A=∠DCE,由等腰三角形的性质可得∠E=∠DCE,据此证明;
(2)连接AC,则AC为直径,由圆周角定理可得∠ABC=90°,根据∠A=∠AEB可得AB=BE=8,由中点的概念可得BC的值,然后利用勾股定理进行计算即可.
10.【答案】(1)各个角;各条边
(2)解:如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24×=;
(3)9;360°
【解析】【解答】解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
【分析】(1)根据正多边形的定义求解即可;
(2)先求出 AB=BC=CD=DE=EF=FA, 再求出 六边形ABCDEFA是正六边形,最后求解即可;
(3)先求出正六边形的对角线条数为9,再求解即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
