24.4 弧长及扇形的面积一课一练(含解析)
文档属性
| 名称 | 24.4 弧长及扇形的面积一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 491.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 07:35:24 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
24.4 弧长及扇形的面积一课一练
一、填空题
1.如图,点O是半圆圆心,是半圆的直径,点A、D在半圆上,且,,,则阴影部分的面积是 .
二、单选题
2.学校图书馆的阅读角有一块半径为3m,圆心角为120°的扇形地毯,这块地毯的面积为( )
A. B. C. D.
3.已知一个扇形的半径长是 ,圆心角为 ,则这个扇形的面积为( )
A. B. C. D.
4.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )
A.π B.1 C.2 D.
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,弧BC长为50πcm,则半径AB的长为( )
A.50cm B.60cm C.120cm D.30cm
6.已知扇形的圆心角为60°,半径为1,则扇形的弧长为( )
A. B.π C. D.
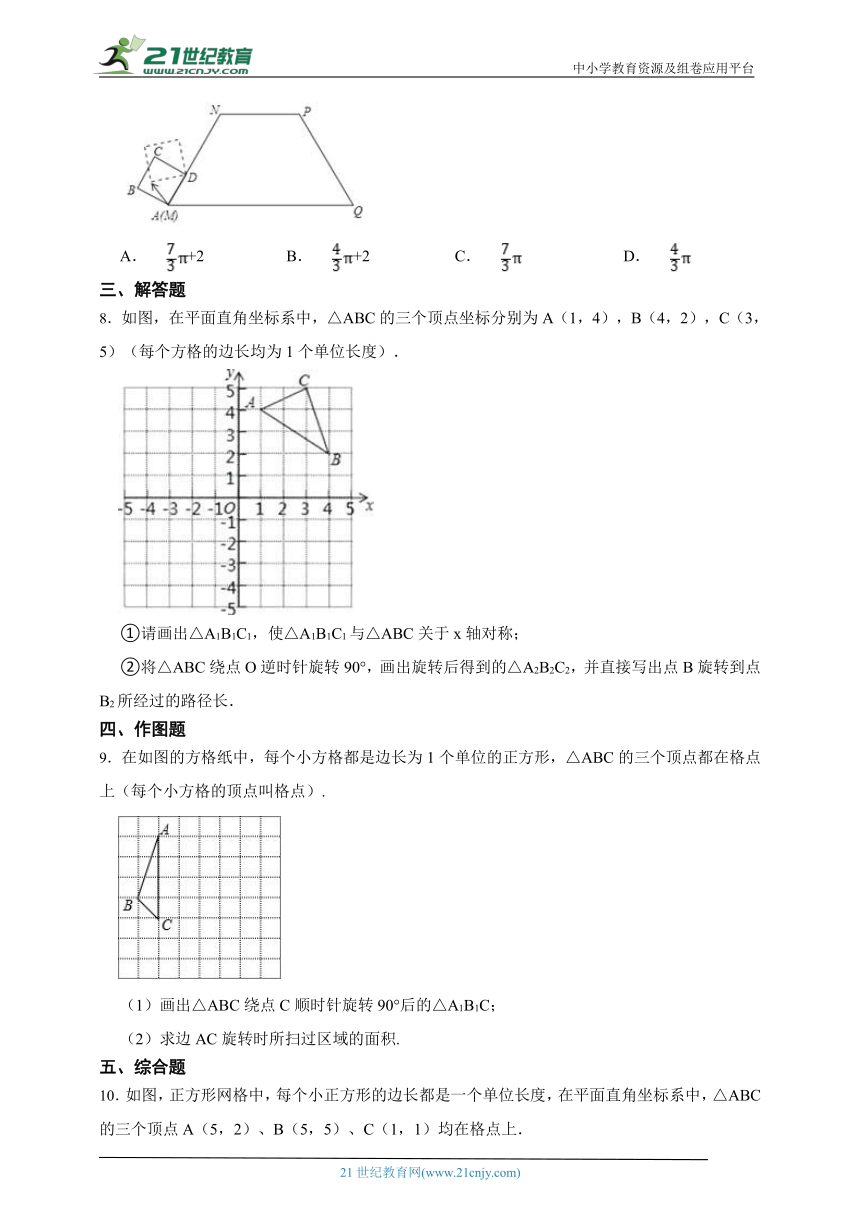
7.如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S=( )
A.+2 B.+2 C. D.
三、解答题
8.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
①请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
四、作图题
9.在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)画出△ABC绕点C顺时针旋转90°后的△A1B1C;
(2)求边AC旋转时所扫过区域的面积.
五、综合题
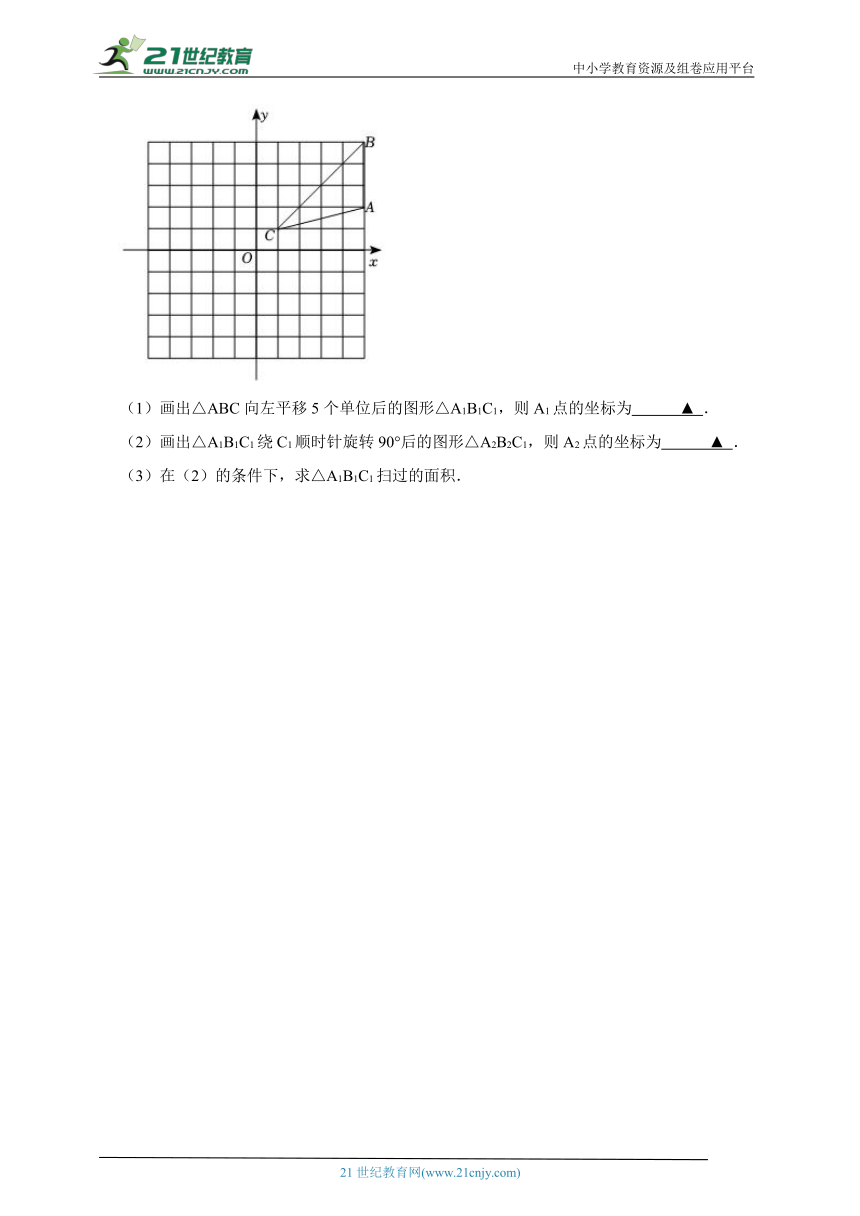
10.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上.
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,则A1点的坐标为 ▲ .
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,则A2点的坐标为 ▲ .
(3)在(2)的条件下,求△A1B1C1扫过的面积.
答案解析部分
1.【答案】
【解析】【解答】解:如图所示:连接OA、OD,
∵∠ABO=60°,OA=OB,AB=4,
∴△AOB是等边三角形,
∴OA=OB=AB=4,∠AOB=60°,
∵AD//BO,
∴∠OAD=∠AOB=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵AD//BO,
∴△OAD与△ABD是同底等高的三角形,
∴,
即阴影部分的面积是,
故答案为:.
【分析】根据题意先求出△AOB是等边三角形,再求出∠AOD=60°,最后利用扇形的面积公式计算求解即可。
2.【答案】C
【解析】【解答】解:钢板的面积,
故答案为:C.
【分析】扇形的面积公式,据此计算即可.
3.【答案】B
【解析】【解答】解:由扇形的面积公式可得,这个扇形的面积为
故答案为:B.
【分析】根据扇形的面积公式S=进行计算即可.
4.【答案】C
【解析】【分析】根据扇形的面积公式计算.
【解答】设扇形的半径为r,
根据扇形面积公式得S=lr=r2=2
故选C.
【点评】本题主要考查了扇形的面积公式.
5.【答案】B
【解析】【解答】由扇形的弧长公式得:
解得:AB=60cm.
故答案为:B.
【分析】已知弧长和扇形圆心角,依据弧长公式即可求解.
6.【答案】D
【解析】【解答】解:根据弧长公式知:扇形的弧长为 .
故答案为:D.
【分析】根据扇形的弧长公式:l=直接计算即可.
7.【答案】A
【解析】【解答】 解:(1)作图如图;
(2)∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、、1,翻转角分别为90°、90°、150°,
∴S=2×
=+π+π+2
=+2.
故选A.
【分析】先根据点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、2、1,翻转角分别为90°、90°、150°,据此画出图形.再结合总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可.
8.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求;
∵OB= ,∠BOB2=90°,
∴点B旋转到点B2所经过的路径长为 .
【解析】【分析】根据轴对称的性质及旋转的性质按要求画出图形即可;点B旋转到点B2所经过的路径长是以O为圆心,圆心角为90°,OB的长为半径的弧,因此先利用勾股定理求出OB的长,再根据扇形的面积公式求出弧BB2的长即可。
9.【答案】(1)解:如图所示,
(2)解:由题意可得,边AC旋转时所扫过区域的面积是 = =4π.
【解析】【分析】(1)根据题意可以画出相应的图形;(2)根据题意可知边AC旋转时所扫过区域是以点C为圆心,CA=4为半径,圆形角为90°的扇形,从而利用扇形面积公式可以解答本题.
10.【答案】(1)解:如图所示,即为所求,
;
由图形可知,A1(0,2);
(2)解:如图所示,即为所求,
;
由图形可知,A2(﹣3,﹣3);
(3)解:∵
而扫过的面积是以为圆心,为半径的圆的面积的 再加上的面积,
∴
【解析】【分析】(1)根据平移的性质找出点A、B、C的对应点,再连接并直接求出点A1的坐标即可;
(2)根据旋转的性质找出点A、B、C的对应点,再连接并直接写出点A2的坐标即可;
(3)利用割补法求出图形的面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
24.4 弧长及扇形的面积一课一练
一、填空题
1.如图,点O是半圆圆心,是半圆的直径,点A、D在半圆上,且,,,则阴影部分的面积是 .
二、单选题
2.学校图书馆的阅读角有一块半径为3m,圆心角为120°的扇形地毯,这块地毯的面积为( )
A. B. C. D.
3.已知一个扇形的半径长是 ,圆心角为 ,则这个扇形的面积为( )
A. B. C. D.
4.如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( )
A.π B.1 C.2 D.
5.如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为150°,弧BC长为50πcm,则半径AB的长为( )
A.50cm B.60cm C.120cm D.30cm
6.已知扇形的圆心角为60°,半径为1,则扇形的弧长为( )
A. B.π C. D.
7.如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动,求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S=( )
A.+2 B.+2 C. D.
三、解答题
8.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
①请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
②将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
四、作图题
9.在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
(1)画出△ABC绕点C顺时针旋转90°后的△A1B1C;
(2)求边AC旋转时所扫过区域的面积.
五、综合题
10.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上.
(1)画出△ABC向左平移5个单位后的图形△A1B1C1,则A1点的坐标为 ▲ .
(2)画出△A1B1C1绕C1顺时针旋转90°后的图形△A2B2C1,则A2点的坐标为 ▲ .
(3)在(2)的条件下,求△A1B1C1扫过的面积.
答案解析部分
1.【答案】
【解析】【解答】解:如图所示:连接OA、OD,
∵∠ABO=60°,OA=OB,AB=4,
∴△AOB是等边三角形,
∴OA=OB=AB=4,∠AOB=60°,
∵AD//BO,
∴∠OAD=∠AOB=60°,
∵OA=OD,
∴△AOD是等边三角形,
∴∠AOD=60°,
∵AD//BO,
∴△OAD与△ABD是同底等高的三角形,
∴,
即阴影部分的面积是,
故答案为:.
【分析】根据题意先求出△AOB是等边三角形,再求出∠AOD=60°,最后利用扇形的面积公式计算求解即可。
2.【答案】C
【解析】【解答】解:钢板的面积,
故答案为:C.
【分析】扇形的面积公式,据此计算即可.
3.【答案】B
【解析】【解答】解:由扇形的面积公式可得,这个扇形的面积为
故答案为:B.
【分析】根据扇形的面积公式S=进行计算即可.
4.【答案】C
【解析】【分析】根据扇形的面积公式计算.
【解答】设扇形的半径为r,
根据扇形面积公式得S=lr=r2=2
故选C.
【点评】本题主要考查了扇形的面积公式.
5.【答案】B
【解析】【解答】由扇形的弧长公式得:
解得:AB=60cm.
故答案为:B.
【分析】已知弧长和扇形圆心角,依据弧长公式即可求解.
6.【答案】D
【解析】【解答】解:根据弧长公式知:扇形的弧长为 .
故答案为:D.
【分析】根据扇形的弧长公式:l=直接计算即可.
7.【答案】A
【解析】【解答】 解:(1)作图如图;
(2)∵点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、、1,翻转角分别为90°、90°、150°,
∴S=2×
=+π+π+2
=+2.
故选A.
【分析】先根据点A绕点D翻滚,然后绕点C翻滚,然后绕点B翻滚,半径分别为1、2、1,翻转角分别为90°、90°、150°,据此画出图形.再结合总结的翻转角度和翻转半径,求出圆弧与梯形的边长围成的扇形的面积即可.
8.【答案】解:如图所示,△A1B1C1、△A2B2C2即为所求;
∵OB= ,∠BOB2=90°,
∴点B旋转到点B2所经过的路径长为 .
【解析】【分析】根据轴对称的性质及旋转的性质按要求画出图形即可;点B旋转到点B2所经过的路径长是以O为圆心,圆心角为90°,OB的长为半径的弧,因此先利用勾股定理求出OB的长,再根据扇形的面积公式求出弧BB2的长即可。
9.【答案】(1)解:如图所示,
(2)解:由题意可得,边AC旋转时所扫过区域的面积是 = =4π.
【解析】【分析】(1)根据题意可以画出相应的图形;(2)根据题意可知边AC旋转时所扫过区域是以点C为圆心,CA=4为半径,圆形角为90°的扇形,从而利用扇形面积公式可以解答本题.
10.【答案】(1)解:如图所示,即为所求,
;
由图形可知,A1(0,2);
(2)解:如图所示,即为所求,
;
由图形可知,A2(﹣3,﹣3);
(3)解:∵
而扫过的面积是以为圆心,为半径的圆的面积的 再加上的面积,
∴
【解析】【分析】(1)根据平移的性质找出点A、B、C的对应点,再连接并直接求出点A1的坐标即可;
(2)根据旋转的性质找出点A、B、C的对应点,再连接并直接写出点A2的坐标即可;
(3)利用割补法求出图形的面积即可。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
