第二十四章 圆综合知识测试题(含解析)
文档属性
| 名称 | 第二十四章 圆综合知识测试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 608.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 07:47:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十四章 圆综合知识测试题
一、填空题
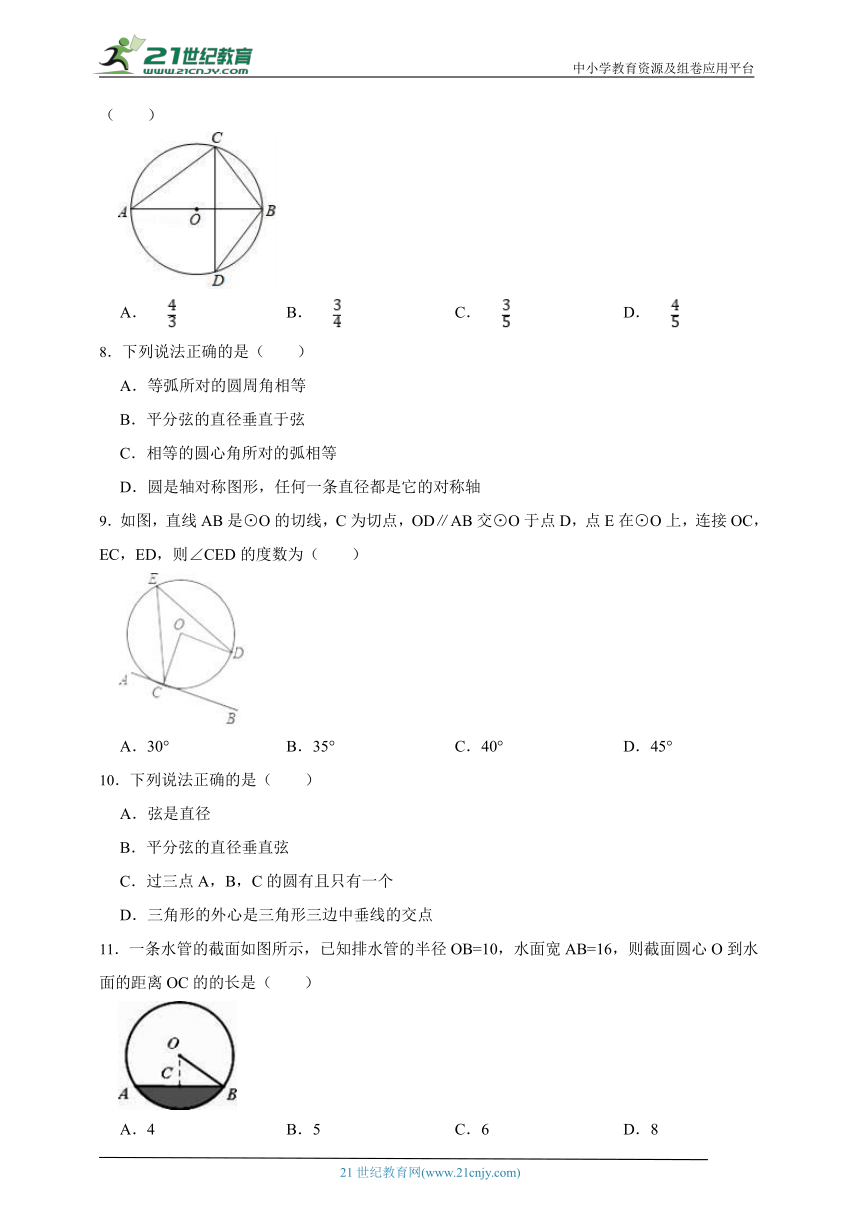
1.如图,AB是⊙O的直径,∠AOC=120°,则∠BDC= .
2.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为 .
二、单选题
3.如图,点A、B、C都在 上,若∠AOB=72°,则∠ACB的度数为()
A.18° B.30° C.36° D.72°
4.若圆的半径是5,点P到圆心的距离为5,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内
C.点P在⊙O上 D.点P在⊙O外或⊙O上
5. 正n边形的一个外角为30°,则n的值为( ).
A.6 B.8 C.10 D.12
6.如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π﹣2 B. C.π﹣4 D.
7.如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=3,AC=4,则sin∠ABD的值是( )
A. B. C. D.
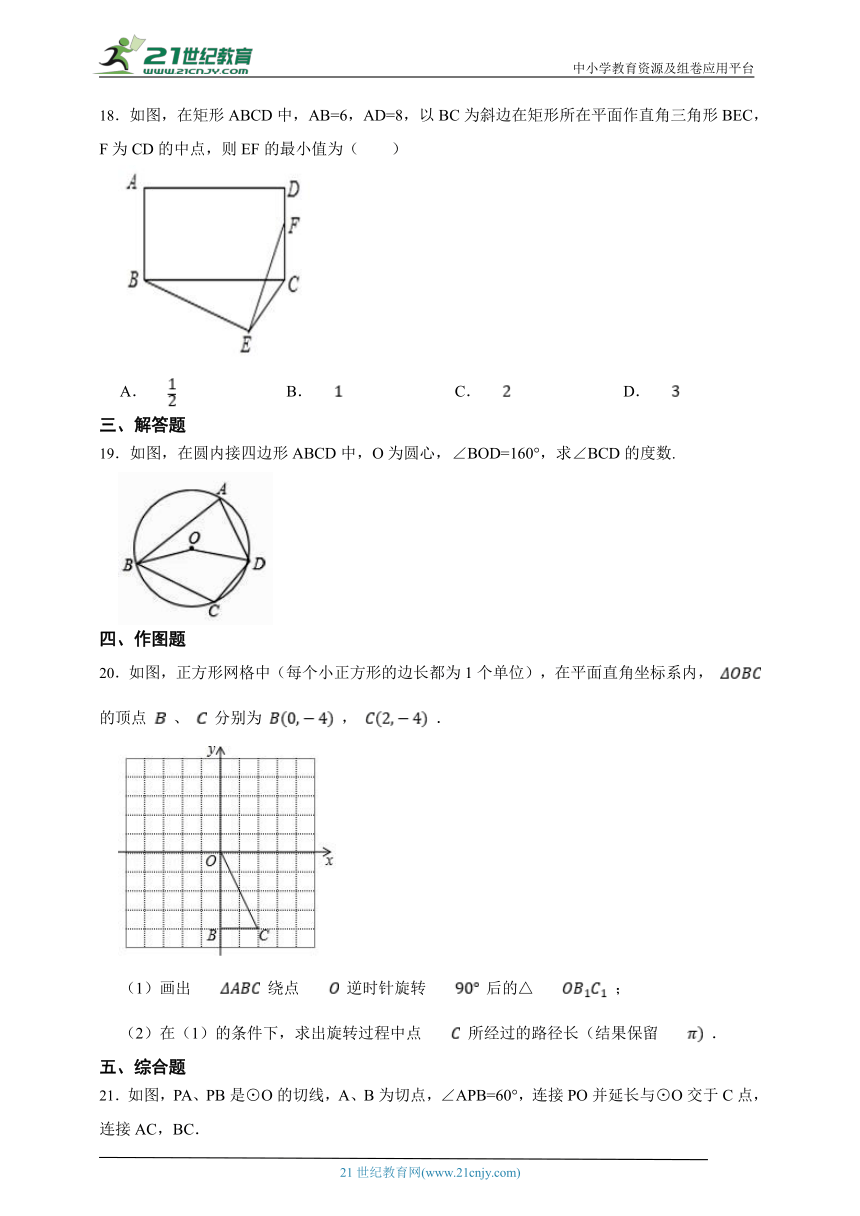
8.下列说法正确的是( )
A.等弧所对的圆周角相等
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.圆是轴对称图形,任何一条直径都是它的对称轴
9.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30° B.35° C.40° D.45°
10.下列说法正确的是( )
A.弦是直径
B.平分弦的直径垂直弦
C.过三点A,B,C的圆有且只有一个
D.三角形的外心是三角形三边中垂线的交点
11.一条水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC的的长是( )
A.4 B.5 C.6 D.8
12.用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )
A.没有一个角不小于60° B.没有一个角不大于60°
C.所有内角不大于60° D.所有内角不小于60°
13.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为( )
A. B. C. D.
14.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
15.下列各图形中,各个顶点一定在同一个圆上的是( )
A.正方形 B.菱形
C.平行四边形 D.梯形
16.如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A.240° B.360° C.480° D.540°
17.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的圆内接多边形是正多边形
18.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为( )
A. B. C. D.
三、解答题
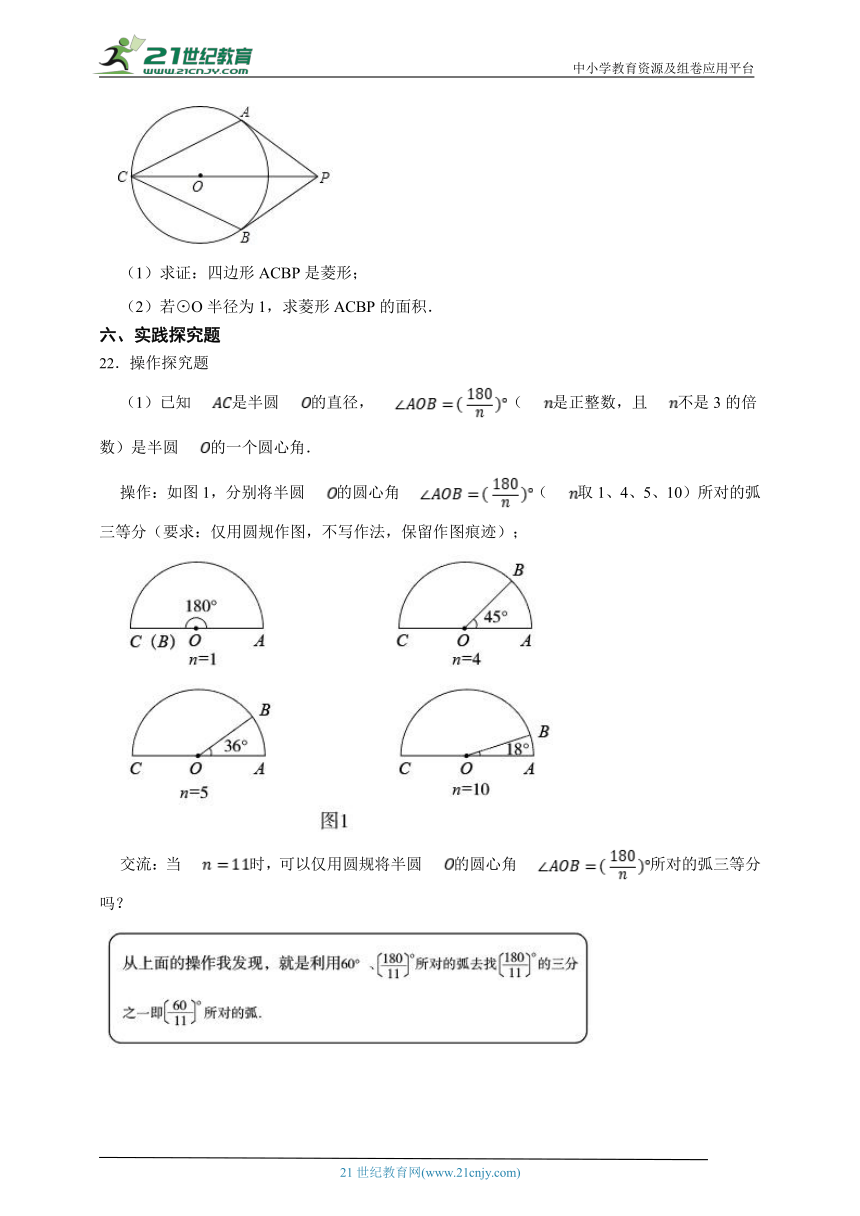
19.如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
四、作图题
20.如图,正方形网格中(每个小正方形的边长都为1个单位),在平面直角坐标系内, 的顶点 、 分别为 , .
(1)画出 绕点 逆时针旋转 后的△ ;
(2)在(1)的条件下,求出旋转过程中点 所经过的路径长(结果保留 .
五、综合题
21.如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
六、实践探究题
22.操作探究题
(1)已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.
操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);
交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)如图2,的圆周角.为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).
答案解析部分
1.【答案】30°
【解析】【解答】根据题意可得:∠BOC=180°-120°=60°,则∠BDC=60°÷2=30°.
【分析】根据平角的定义可以求出∠BOC的度数,再根据同弧所对的圆心角的度数等于圆周角度数的2倍.即可得出答案。
2.【答案】130°
【解析】【解答】解:∵∠ACD=25 ,
∴∠AOD=50 ,
∴∠BOD=180 -∠AOD=130 .
故答案为130 .
【分析】先根据在同圆或等圆当中,同弧所对的圆周角等于圆心角的一半求出∠AOD=50 ,再利用临补角求出答案即可。
3.【答案】C
【解析】【解答】解:∵∠AOB=72°,
∴∠ACB= ∠AOB=36°,
故答案为:C.
【分析】根据一条弧所对的的圆周角等于它所对圆心角的一半进行解答即可.
4.【答案】C
【解析】【解答】解:∵圆的半径是5,点P到圆心的距离为5,
∴d=r,
∴点P在⊙O上.
故答案为:C.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此判断即可.
5.【答案】D
【解析】【解答】解:n=360°÷30°=12.
故答案为:D.
【分析】由于正多边形的每一个外角都相等,故用多边形的外角和除以一个外角的度数即可求出多边形的边数.
6.【答案】A
【解析】【解答】解:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴S阴影=S扇形OBC﹣S△OBC= π×22﹣ ×2×2=π﹣2.
故答案为:A
【分析】先证得△OBC是等腰直角三角形,然后根据S阴影=S扇形OBC﹣S△OBC即可求得
7.【答案】D
【解析】【解答】∵AB是⊙O的直径,CD⊥AB,
∴弧AC=弧AD,
∴∠ABD=∠ABC.
根据勾股定理求得AB=5,
∴sin∠ABD=sin∠ABC= .
故答案为:D.
【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC,再根据勾股定理求得AB=5,即可求sin∠ABD的值.
8.【答案】A
【解析】【解答】解:A. 同弧或等弧所对的圆周角相等,所以A选项正确;
B.平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,所以B选项错误;
C、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所以C选项错误;
D.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以D选项错误.
故答案为:A.
【分析】A. 同弧或等弧所对的圆周角相等,据此判断即可;
B.平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,据此判断即可;
C、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,据此判断即可;
D.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,据此判断即可.
9.【答案】D
【解析】【解答】解:∵直线AB是⊙O的切线,C为切点,
∴∠OCB=90°,
∵OD∥AB,
∴∠COD=90°,
∴∠CED= ∠COD=45°,
故答案为:D.
【分析】根据切线的性质得出∠OCB=90°根据二直线平行,同旁内角互补得出∠COD=90°,根据同弧所对的圆周角是圆心角的一半得出答案。
10.【答案】D
【解析】【分析】利用弦的定义、垂径定理以及不在同一直线上的三点确定一个圆即可作出判断.
【解答】A、弦是圆上任意两点的连线,而圆是过圆心的弦,故弦不一定是直径,故选项错误;
B、平分弦(弦不是直径)的直径垂直于弦,故选项错误;
C、过不在一条直线上的三点的圆有且只有一个,故选项错误;
D、正确.
故选D.
【点评】本题考查了弦的定义、垂径定理以及不在同一直线上的三点确定一个圆,要注意到垂径定理叙述中:被平分的弦必须不是直径
11.【答案】C
【解析】【解答】解:∵OC⊥AB,
∴BC= ,
在Rt△OBC中,OC= .
故答案为:C.
【分析】由OC⊥AB,符合垂径定理,即经过O,C的直径平分弦AB,即BC= ,再由勾股定理算出OC即可.
12.【答案】B
【解析】【解答】解:用反证法证明“三角形中必有一个内角不小于60°”时,应先假设三角形中每一个内角都大于60°.
故答案为:B.
【分析】反证法的第一步是假设命题的结论不成立,据此可以得到答案.
13.【答案】B
【解析】【解答】解:如图所示,连接OA,OB,
∵∠C=30°,
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2,
∴圆O的半径为2,
故答案为:B.
【分析】连接OA,OB,根据圆周角的性质可得∠OAB=2∠C=60°,所以△OAB是等边三角形,即可得到OA=AB=2。
14.【答案】A
【解析】【解答】正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;各边都相等的多边形不一定是正多边形.
【分析】此题考查正多边形的定义,熟练掌握定义是解题的关键.
15.【答案】A
【解析】【解答】∵正方形对角线相等且互相平分,∴四个顶点到对角线交点距离相等,∴正方形四个顶点定可在同一个圆上.故选:A.
【分析】四个顶点可在同一个圆上的四边形,一定有一点到它的四个顶点的距离都相等,因而B、C、D都是错误的;正方形的四个顶点到对角线的交点的距离都相同,因而正方形的四个顶点一定可以在同一个圆上.
16.【答案】C
【解析】【解答】解:由题意可得:第一次AO顺时针转动了120°,第二次AO顺时针转动了240°,第三次AO顺时针转动了120°,
故当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是:120°+240°+120°=480°.
故选:C.
【分析】根据正三角形的性质分别得出点O转动的角度,进而得出答案.
17.【答案】C
【解析】【解答】∵各边相等,各角也相等的多边形叫做正多边形,∴A、B错误;∵各边相等的圆内接多边形的各角一定相等,∴C正确;∵各角相等的圆内接多边形的边不一定相同,∴D错误.故选C.
【分析】根据正多边形的定义对各选项进行逐一分析即可.
18.【答案】B
【解析】【解答】解:如图,当F、E、O三点在一条直线上时,EF最短,
这时OF2=FC2+OC2=32+42=25,
∴OF=5,
∴EF=OF-OE=5-4=1.
故答案为:B.
【分析】过BC的中点O作圆,连接OF交圆于点E,这时EF为最短,在Rt△OCF中,运用勾股定理求出OF的长,则EF等于OF于OE的长度之差.
19.【答案】解:∵∠BOD=160°∴∠BAD=
∵A、B、C、D四点共圆,
∴∠BCD+∠BAD=180°,
∴∠BCD=100°.
【解析】【分析】由圆周角定理得∠BAD=∠BOD,再根据圆内接四边形的对角互补可求得∠BCD的度数。
20.【答案】(1)解:如图所示:△ ,即为所求
(2)解:旋转过程中点 所经过分路径长为: .
【解析】【分析】(1)利用旋转的性质得出对应点位置进而得出答案;(2)利用弧长求法得出答案
21.【答案】(1)解:连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO= ∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)解:连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD= OA= ,
∴PD= ,
∴PC=3,AB= ,
∴菱形ACBP的面积= AB PC=
【解析】【分析】(1)连接AO,BO,根据PA、PB是⊙O的切线,得到∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO= ∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;(2)连接AB交PC于D,根据菱形的性质得到AD⊥PC,解直角三角形即可得到结论.
22.【答案】(1)解:操作:
交流: ,或 ;
探究:设 ,解得 ( 为非负整数).
或设 ,解得 ( 为正整数).
所以对于正整数 ( 不是3的倍数),都可以仅用圆规将半圆 的圆心角 所对的弧三等分;
(2)解:如图
【解析】【分析】(1)操作:分别构造60°弧、15°弧、12°弧、6°弧即可解决问题;
交流:当n=28时,三者之间的数量关系为;
探究:设 或设,用含k的式子表示出n即可;
(2)以P为端点,用半径去截圆,与圆交于一点,再以该点为端点,重复上述步骤,得到点D,以Q为圆心,QP为半径画弧,与圆交于一点C,则弧即为所作.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二十四章 圆综合知识测试题
一、填空题
1.如图,AB是⊙O的直径,∠AOC=120°,则∠BDC= .
2.如图,AB是⊙O的直径,点C、D在⊙O上,若∠ACD=25°,则∠BOD的度数为 .
二、单选题
3.如图,点A、B、C都在 上,若∠AOB=72°,则∠ACB的度数为()
A.18° B.30° C.36° D.72°
4.若圆的半径是5,点P到圆心的距离为5,则点P与⊙O的位置关系是( )
A.点P在⊙O外 B.点P在⊙O内
C.点P在⊙O上 D.点P在⊙O外或⊙O上
5. 正n边形的一个外角为30°,则n的值为( ).
A.6 B.8 C.10 D.12
6.如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A.π﹣2 B. C.π﹣4 D.
7.如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=3,AC=4,则sin∠ABD的值是( )
A. B. C. D.
8.下列说法正确的是( )
A.等弧所对的圆周角相等
B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等
D.圆是轴对称图形,任何一条直径都是它的对称轴
9.如图,直线AB是⊙O的切线,C为切点,OD∥AB交⊙O于点D,点E在⊙O上,连接OC,EC,ED,则∠CED的度数为( )
A.30° B.35° C.40° D.45°
10.下列说法正确的是( )
A.弦是直径
B.平分弦的直径垂直弦
C.过三点A,B,C的圆有且只有一个
D.三角形的外心是三角形三边中垂线的交点
11.一条水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC的的长是( )
A.4 B.5 C.6 D.8
12.用反证法证明“三角形中至少有一个内角不大于60°”,首先应假设这个三角形中( )
A.没有一个角不小于60° B.没有一个角不大于60°
C.所有内角不大于60° D.所有内角不小于60°
13.如图,△ABC内接于⊙O,∠C=30°,AB=2,则⊙O的半径为( )
A. B. C. D.
14.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
15.下列各图形中,各个顶点一定在同一个圆上的是( )
A.正方形 B.菱形
C.平行四边形 D.梯形
16.如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
A.240° B.360° C.480° D.540°
17.下列说法正确的是( )
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.各边相等的圆内接多边形是正多边形
D.各角相等的圆内接多边形是正多边形
18.如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形所在平面作直角三角形BEC,F为CD的中点,则EF的最小值为( )
A. B. C. D.
三、解答题
19.如图,在圆内接四边形ABCD中,O为圆心,∠BOD=160°,求∠BCD的度数.
四、作图题
20.如图,正方形网格中(每个小正方形的边长都为1个单位),在平面直角坐标系内, 的顶点 、 分别为 , .
(1)画出 绕点 逆时针旋转 后的△ ;
(2)在(1)的条件下,求出旋转过程中点 所经过的路径长(结果保留 .
五、综合题
21.如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;
(2)若⊙O半径为1,求菱形ACBP的面积.
六、实践探究题
22.操作探究题
(1)已知是半圆的直径,(是正整数,且不是3的倍数)是半圆的一个圆心角.
操作:如图1,分别将半圆的圆心角(取1、4、5、10)所对的弧三等分(要求:仅用圆规作图,不写作法,保留作图痕迹);
交流:当时,可以仅用圆规将半圆的圆心角所对的弧三等分吗?
探究:你认为当满足什么条件时,就可以仅用圆规将半圆的圆心角所对的弧三等分?说说你的理由.
(2)如图2,的圆周角.为了将这个圆的圆周14等分,请作出它的一条14等分弧(要求:仅用圆规作图,不写作法,保留作图痕迹).
答案解析部分
1.【答案】30°
【解析】【解答】根据题意可得:∠BOC=180°-120°=60°,则∠BDC=60°÷2=30°.
【分析】根据平角的定义可以求出∠BOC的度数,再根据同弧所对的圆心角的度数等于圆周角度数的2倍.即可得出答案。
2.【答案】130°
【解析】【解答】解:∵∠ACD=25 ,
∴∠AOD=50 ,
∴∠BOD=180 -∠AOD=130 .
故答案为130 .
【分析】先根据在同圆或等圆当中,同弧所对的圆周角等于圆心角的一半求出∠AOD=50 ,再利用临补角求出答案即可。
3.【答案】C
【解析】【解答】解:∵∠AOB=72°,
∴∠ACB= ∠AOB=36°,
故答案为:C.
【分析】根据一条弧所对的的圆周角等于它所对圆心角的一半进行解答即可.
4.【答案】C
【解析】【解答】解:∵圆的半径是5,点P到圆心的距离为5,
∴d=r,
∴点P在⊙O上.
故答案为:C.
【分析】设⊙O的半径为r,点到圆心O的距离为d,当d<r时,点在圆内;当d=r时,点在圆上,当d>r时,点在圆外,据此判断即可.
5.【答案】D
【解析】【解答】解:n=360°÷30°=12.
故答案为:D.
【分析】由于正多边形的每一个外角都相等,故用多边形的外角和除以一个外角的度数即可求出多边形的边数.
6.【答案】A
【解析】【解答】解:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴S阴影=S扇形OBC﹣S△OBC= π×22﹣ ×2×2=π﹣2.
故答案为:A
【分析】先证得△OBC是等腰直角三角形,然后根据S阴影=S扇形OBC﹣S△OBC即可求得
7.【答案】D
【解析】【解答】∵AB是⊙O的直径,CD⊥AB,
∴弧AC=弧AD,
∴∠ABD=∠ABC.
根据勾股定理求得AB=5,
∴sin∠ABD=sin∠ABC= .
故答案为:D.
【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC,再根据勾股定理求得AB=5,即可求sin∠ABD的值.
8.【答案】A
【解析】【解答】解:A. 同弧或等弧所对的圆周角相等,所以A选项正确;
B.平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,所以B选项错误;
C、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,所以C选项错误;
D.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,所以D选项错误.
故答案为:A.
【分析】A. 同弧或等弧所对的圆周角相等,据此判断即可;
B.平分弦(非直径)的直径垂直于弦,并且平分弦所对的弧,据此判断即可;
C、在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦相等,据此判断即可;
D.圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,据此判断即可.
9.【答案】D
【解析】【解答】解:∵直线AB是⊙O的切线,C为切点,
∴∠OCB=90°,
∵OD∥AB,
∴∠COD=90°,
∴∠CED= ∠COD=45°,
故答案为:D.
【分析】根据切线的性质得出∠OCB=90°根据二直线平行,同旁内角互补得出∠COD=90°,根据同弧所对的圆周角是圆心角的一半得出答案。
10.【答案】D
【解析】【分析】利用弦的定义、垂径定理以及不在同一直线上的三点确定一个圆即可作出判断.
【解答】A、弦是圆上任意两点的连线,而圆是过圆心的弦,故弦不一定是直径,故选项错误;
B、平分弦(弦不是直径)的直径垂直于弦,故选项错误;
C、过不在一条直线上的三点的圆有且只有一个,故选项错误;
D、正确.
故选D.
【点评】本题考查了弦的定义、垂径定理以及不在同一直线上的三点确定一个圆,要注意到垂径定理叙述中:被平分的弦必须不是直径
11.【答案】C
【解析】【解答】解:∵OC⊥AB,
∴BC= ,
在Rt△OBC中,OC= .
故答案为:C.
【分析】由OC⊥AB,符合垂径定理,即经过O,C的直径平分弦AB,即BC= ,再由勾股定理算出OC即可.
12.【答案】B
【解析】【解答】解:用反证法证明“三角形中必有一个内角不小于60°”时,应先假设三角形中每一个内角都大于60°.
故答案为:B.
【分析】反证法的第一步是假设命题的结论不成立,据此可以得到答案.
13.【答案】B
【解析】【解答】解:如图所示,连接OA,OB,
∵∠C=30°,
∴∠OAB=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴OA=AB=2,
∴圆O的半径为2,
故答案为:B.
【分析】连接OA,OB,根据圆周角的性质可得∠OAB=2∠C=60°,所以△OAB是等边三角形,即可得到OA=AB=2。
14.【答案】A
【解析】【解答】正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;各边都相等的多边形不一定是正多边形.
【分析】此题考查正多边形的定义,熟练掌握定义是解题的关键.
15.【答案】A
【解析】【解答】∵正方形对角线相等且互相平分,∴四个顶点到对角线交点距离相等,∴正方形四个顶点定可在同一个圆上.故选:A.
【分析】四个顶点可在同一个圆上的四边形,一定有一点到它的四个顶点的距离都相等,因而B、C、D都是错误的;正方形的四个顶点到对角线的交点的距离都相同,因而正方形的四个顶点一定可以在同一个圆上.
16.【答案】C
【解析】【解答】解:由题意可得:第一次AO顺时针转动了120°,第二次AO顺时针转动了240°,第三次AO顺时针转动了120°,
故当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是:120°+240°+120°=480°.
故选:C.
【分析】根据正三角形的性质分别得出点O转动的角度,进而得出答案.
17.【答案】C
【解析】【解答】∵各边相等,各角也相等的多边形叫做正多边形,∴A、B错误;∵各边相等的圆内接多边形的各角一定相等,∴C正确;∵各角相等的圆内接多边形的边不一定相同,∴D错误.故选C.
【分析】根据正多边形的定义对各选项进行逐一分析即可.
18.【答案】B
【解析】【解答】解:如图,当F、E、O三点在一条直线上时,EF最短,
这时OF2=FC2+OC2=32+42=25,
∴OF=5,
∴EF=OF-OE=5-4=1.
故答案为:B.
【分析】过BC的中点O作圆,连接OF交圆于点E,这时EF为最短,在Rt△OCF中,运用勾股定理求出OF的长,则EF等于OF于OE的长度之差.
19.【答案】解:∵∠BOD=160°∴∠BAD=
∵A、B、C、D四点共圆,
∴∠BCD+∠BAD=180°,
∴∠BCD=100°.
【解析】【分析】由圆周角定理得∠BAD=∠BOD,再根据圆内接四边形的对角互补可求得∠BCD的度数。
20.【答案】(1)解:如图所示:△ ,即为所求
(2)解:旋转过程中点 所经过分路径长为: .
【解析】【分析】(1)利用旋转的性质得出对应点位置进而得出答案;(2)利用弧长求法得出答案
21.【答案】(1)解:连接AO,BO,
∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO= ∠APB=30°,
∴∠AOP=60°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠AOP=∠CAO+∠ACO,
∴∠ACO=30°,
∴∠ACO=∠APO,
∴AC=AP,
同理BC=PB,
∴AC=BC=BP=AP,
∴四边形ACBP是菱形;
(2)解:连接AB交PC于D,
∴AD⊥PC,
∴OA=1,∠AOP=60°,
∴AD= OA= ,
∴PD= ,
∴PC=3,AB= ,
∴菱形ACBP的面积= AB PC=
【解析】【分析】(1)连接AO,BO,根据PA、PB是⊙O的切线,得到∠OAP=∠OBP=90°,PA=PB,∠APO=∠BPO= ∠APB=30°,由三角形的内角和得到∠AOP=60°,根据三角形外角的性质得到∠ACO=30°,得到AC=AP,同理BC=PB,于是得到结论;(2)连接AB交PC于D,根据菱形的性质得到AD⊥PC,解直角三角形即可得到结论.
22.【答案】(1)解:操作:
交流: ,或 ;
探究:设 ,解得 ( 为非负整数).
或设 ,解得 ( 为正整数).
所以对于正整数 ( 不是3的倍数),都可以仅用圆规将半圆 的圆心角 所对的弧三等分;
(2)解:如图
【解析】【分析】(1)操作:分别构造60°弧、15°弧、12°弧、6°弧即可解决问题;
交流:当n=28时,三者之间的数量关系为;
探究:设 或设,用含k的式子表示出n即可;
(2)以P为端点,用半径去截圆,与圆交于一点,再以该点为端点,重复上述步骤,得到点D,以Q为圆心,QP为半径画弧,与圆交于一点C,则弧即为所作.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
