25.2 用列举法求概率一课一练(含解析)
文档属性
| 名称 | 25.2 用列举法求概率一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 601.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
25.2 用列举法求概率一课一练
一、单选题
1.抛掷一枚质地均匀的普通骰子2次,朝上一面的点数之和可能为2,3,4,5,6,7,8,9,10,11,12,其中概率最大的是( )
A.5 B.6 C.7 D.8
2.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机地放入其中两个信封里,则信封与信编号都相同的概率为( )
A. B. C. D.
3.“学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )
A. B. C. D.
4.从1、2、3、4四个数中随机选取两个不同的数,分别记为 , ,则满足 的概率为( )
A. B. C. D.
二、填空题
5.一个不透明的袋子中装有3个红球,2个白球,小球除颜色外其他均相同,若同时从袋子中任取2个小球,则恰为一个红球,一个白球的概率为
6.某校九年一班班委会有2名男生和若干名女生,班级准备选派2名班委会成员参加学校诗词比赛,若选派一名男生和一名女生的概率为 ,则班委会女生
有 人.
三、计算题
7.在四编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中机抽取一张.
我们知道,满足 的三个正整数a,b,c成为勾股数,请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率(卡片用A,B,C,D表示).
四、解答题
8.一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
五、作图题
9.为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
六、综合题
10.现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“易腐垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率(画树状图或列表求解)
答案解析部分
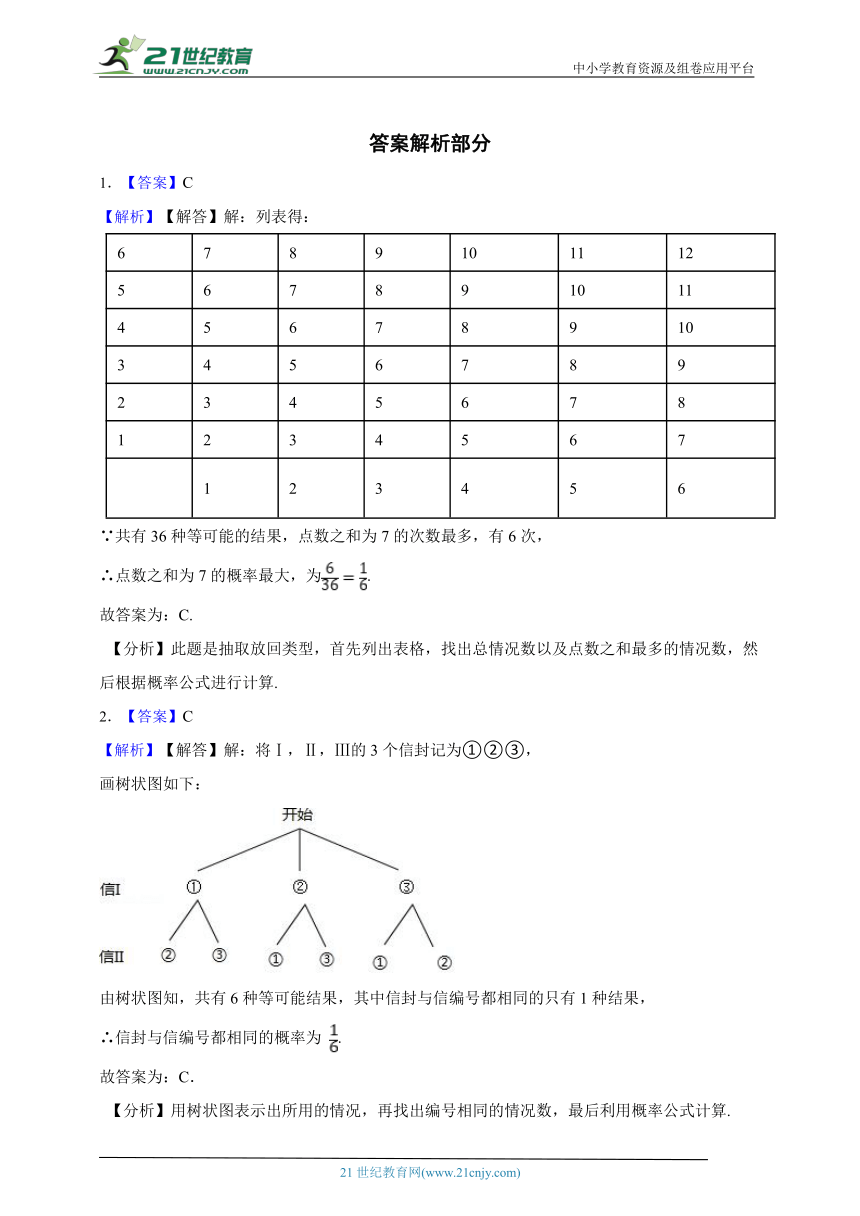
1.【答案】C
【解析】【解答】解:列表得:
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
1 2 3 4 5 6
∵共有36种等可能的结果,点数之和为7的次数最多,有6次,
∴点数之和为7的概率最大,为.
故答案为:C.
【分析】此题是抽取放回类型,首先列出表格,找出总情况数以及点数之和最多的情况数,然后根据概率公式进行计算.
2.【答案】C
【解析】【解答】解:将Ⅰ,Ⅱ,Ⅲ的3个信封记为①②③,
画树状图如下:
由树状图知,共有6种等可能结果,其中信封与信编号都相同的只有1种结果,
∴信封与信编号都相同的概率为 .
故答案为:C.
【分析】用树状图表示出所用的情况,再找出编号相同的情况数,最后利用概率公式计算.
3.【答案】A
【解析】【解答】解:画树状图为:(用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆)
共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,
所以两人恰好选择同一场馆的概率= = 。
故答案为:A。
【分析】用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆,根据题意画出树状图,由图可知共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,根据概率公式即可算出答案。
4.【答案】C
【解析】【解答】如图:符合 的共有6种情况,
而a、c的组合共有12种,
故这两人有“心灵感应”的概率为 .
故答案为:C.
【分析】根据题意列出树状图,得到所有a、c的组合再找到满足 的数对即可.
5.【答案】
【解析】【解答】解:列表如下:
共有20种等可能结果,其中符合题意的有12种
∴恰为一个红球,一个白球的概率为:
故答案为: .
【分析】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
6.【答案】2
【解析】【解答】解:画树状图如下:
由树形图可知:P(恰好为1名男生和1名女生)= = .
故答案为:2.
【分析】根据题意可直接先画出列表或树状图,根据图可判断12种结果中有8种结果可以使该事件发生,即可得概率.
7.【答案】解:所有可能出现的结果列表如下:
第二次第一次
总共有12种结果,每种结果出现的可能性相同,
其中两张卡片上的数都是勾股数的结果有6种
∴P(两张卡片上的数都是勾股数) .
【解析】【分析】先列表,再求出总共有12种结果,每种结果出现的可能性相同,最后求解即可。
8.【答案】解:(1)画树状图得:
∵共有12种等可能的结果,所指数字之和小于4的有3种情况,
∴P(和小于4)==,
∴小颖参加比赛的概率为:;
(2)不公平,
∵P(小颖)=,
P(小亮)=.
∴P(和小于4)≠P(和大于等于4),
∴游戏不公平;
可改为:若两个数字之和小于5,则小颖去参赛;否则,小亮去参赛.
【解析】【分析】(1)首先根据题意画出树状图,由树状图求得所有等可能的结果与两指针所指数字之和和小于4的情况,则可求得小颖参加比赛的概率;
(2)根据小颖获胜与小亮获胜的概率,比较概率是否相等,即可判定游戏是否公平;使游戏公平,只要概率相等即可.
9.【答案】(1)解:∵被调查的总人数为5÷10%=50(人),
∴看电视的人数为50﹣(15+20+5)=10(人),
补全图形如下:
(2)解:2400× =480(人),
所以估计该校喜爱看电视的学生人数为480人
(3)解:画树状图为:
共有12种等可能的结果数,其中恰好抽到2名男生的结果数为6,
所以恰好抽到2名男生的概率= =
【解析】【分析】(1)先求出被调查的总人数,再根据各项目人数之和等于总人数可得看电视的人数,据此可补全条形图;(2)用总人数乘以样本中看电视人数所占比例可估计该校喜爱看电视的学生人数;(3)画树状图展示12种等可能的结果数,再找出恰好抽到2名男生的结果数,然后根据概率公式求解
10.【答案】(1)解:生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾恰好是“易腐垃圾”类:“易腐垃圾”的概率为:
(2)解:记四种垃圾分别为A、B、C、D,
树状图如下
由树状图知,小丽投放垃圾共有16种等可能结果,其中小丽投放的两袋垃圾不同类的有12种结果,所以小丽投放的两袋垃圾不同类的概率为P=
【解析】【分析】(1)根据生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾,进行计算求解即可;
(2)先画树状图求出小丽投放垃圾共有16种等可能结果,再求概率即可作答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
25.2 用列举法求概率一课一练
一、单选题
1.抛掷一枚质地均匀的普通骰子2次,朝上一面的点数之和可能为2,3,4,5,6,7,8,9,10,11,12,其中概率最大的是( )
A.5 B.6 C.7 D.8
2.有编号为Ⅰ,Ⅱ,Ⅲ的3个信封,现将编号为Ⅰ,Ⅱ的两封信,随机地放入其中两个信封里,则信封与信编号都相同的概率为( )
A. B. C. D.
3.“学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )
A. B. C. D.
4.从1、2、3、4四个数中随机选取两个不同的数,分别记为 , ,则满足 的概率为( )
A. B. C. D.
二、填空题
5.一个不透明的袋子中装有3个红球,2个白球,小球除颜色外其他均相同,若同时从袋子中任取2个小球,则恰为一个红球,一个白球的概率为
6.某校九年一班班委会有2名男生和若干名女生,班级准备选派2名班委会成员参加学校诗词比赛,若选派一名男生和一名女生的概率为 ,则班委会女生
有 人.
三、计算题
7.在四编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中机抽取一张.
我们知道,满足 的三个正整数a,b,c成为勾股数,请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率(卡片用A,B,C,D表示).
四、解答题
8.一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.
五、作图题
9.为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
六、综合题
10.现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“易腐垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率(画树状图或列表求解)
答案解析部分
1.【答案】C
【解析】【解答】解:列表得:
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
1 2 3 4 5 6
∵共有36种等可能的结果,点数之和为7的次数最多,有6次,
∴点数之和为7的概率最大,为.
故答案为:C.
【分析】此题是抽取放回类型,首先列出表格,找出总情况数以及点数之和最多的情况数,然后根据概率公式进行计算.
2.【答案】C
【解析】【解答】解:将Ⅰ,Ⅱ,Ⅲ的3个信封记为①②③,
画树状图如下:
由树状图知,共有6种等可能结果,其中信封与信编号都相同的只有1种结果,
∴信封与信编号都相同的概率为 .
故答案为:C.
【分析】用树状图表示出所用的情况,再找出编号相同的情况数,最后利用概率公式计算.
3.【答案】A
【解析】【解答】解:画树状图为:(用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆)
共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,
所以两人恰好选择同一场馆的概率= = 。
故答案为:A。
【分析】用A、B、C分别表示“图书馆,博物馆,科技馆”三个场馆,根据题意画出树状图,由图可知共有9种等可能的结果数,其中两人恰好选择同一场馆的结果数为3,根据概率公式即可算出答案。
4.【答案】C
【解析】【解答】如图:符合 的共有6种情况,
而a、c的组合共有12种,
故这两人有“心灵感应”的概率为 .
故答案为:C.
【分析】根据题意列出树状图,得到所有a、c的组合再找到满足 的数对即可.
5.【答案】
【解析】【解答】解:列表如下:
共有20种等可能结果,其中符合题意的有12种
∴恰为一个红球,一个白球的概率为:
故答案为: .
【分析】根据随机事件概率大小的求法,找准两点:①符合条件的情况数目;②全部情况的总数.二者的比值就是其发生的概率的大小.
6.【答案】2
【解析】【解答】解:画树状图如下:
由树形图可知:P(恰好为1名男生和1名女生)= = .
故答案为:2.
【分析】根据题意可直接先画出列表或树状图,根据图可判断12种结果中有8种结果可以使该事件发生,即可得概率.
7.【答案】解:所有可能出现的结果列表如下:
第二次第一次
总共有12种结果,每种结果出现的可能性相同,
其中两张卡片上的数都是勾股数的结果有6种
∴P(两张卡片上的数都是勾股数) .
【解析】【分析】先列表,再求出总共有12种结果,每种结果出现的可能性相同,最后求解即可。
8.【答案】解:(1)画树状图得:
∵共有12种等可能的结果,所指数字之和小于4的有3种情况,
∴P(和小于4)==,
∴小颖参加比赛的概率为:;
(2)不公平,
∵P(小颖)=,
P(小亮)=.
∴P(和小于4)≠P(和大于等于4),
∴游戏不公平;
可改为:若两个数字之和小于5,则小颖去参赛;否则,小亮去参赛.
【解析】【分析】(1)首先根据题意画出树状图,由树状图求得所有等可能的结果与两指针所指数字之和和小于4的情况,则可求得小颖参加比赛的概率;
(2)根据小颖获胜与小亮获胜的概率,比较概率是否相等,即可判定游戏是否公平;使游戏公平,只要概率相等即可.
9.【答案】(1)解:∵被调查的总人数为5÷10%=50(人),
∴看电视的人数为50﹣(15+20+5)=10(人),
补全图形如下:
(2)解:2400× =480(人),
所以估计该校喜爱看电视的学生人数为480人
(3)解:画树状图为:
共有12种等可能的结果数,其中恰好抽到2名男生的结果数为6,
所以恰好抽到2名男生的概率= =
【解析】【分析】(1)先求出被调查的总人数,再根据各项目人数之和等于总人数可得看电视的人数,据此可补全条形图;(2)用总人数乘以样本中看电视人数所占比例可估计该校喜爱看电视的学生人数;(3)画树状图展示12种等可能的结果数,再找出恰好抽到2名男生的结果数,然后根据概率公式求解
10.【答案】(1)解:生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾恰好是“易腐垃圾”类:“易腐垃圾”的概率为:
(2)解:记四种垃圾分别为A、B、C、D,
树状图如下
由树状图知,小丽投放垃圾共有16种等可能结果,其中小丽投放的两袋垃圾不同类的有12种结果,所以小丽投放的两袋垃圾不同类的概率为P=
【解析】【分析】(1)根据生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、易腐垃圾、其他垃圾、可回收垃圾,进行计算求解即可;
(2)先画树状图求出小丽投放垃圾共有16种等可能结果,再求概率即可作答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
