25.3 用频率估计概率一课一练(含解析)
文档属性
| 名称 | 25.3 用频率估计概率一课一练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 243.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
25.3 用频率估计概率一课一练
一、填空题
1.当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔逊(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率约为0.5,则掷一枚均匀的硬币,正面朝上的概率是 .
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:
摸球的次数m 100 150 200 500 800 1000
摸到白球的次数n 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中黑球有 个,白球有 个.
二、单选题
3.在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个
A.10 B.15 C.20 D.25
4.在一个不透明的布袋中装有红色.白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到白色球的频率稳定在85%左右,则口袋中红色球可能有( ).
A.34个 B.30个 C.10个 D.6个
5.抛掷一枚质地均匀的硬币时,正面向上的概率是0.5.则下列判断正确的是( )
A.连续掷2次时,正面朝上一定会出现1次
B.连续掷100次时,正面朝上一定会出现50次
C.连续掷次时,正面朝上一定会出现次
D.当抛掷次数越大时,正面朝上的频率越稳定于0.5
6.下表记录了一名球员在罚球线上投篮的结果:
投篮次数 50 100 150 200 250 400 500 800
投中次数 28 63 87 122 148 242 301 480
投中频率 0.560 0.630 0.580 0.610 0.592 0.605 0.602 0.600
根据频率的稳定性,估计这名球员投篮一次投中的概率约是( )
A.0.560 B.0.580 C.0.600 D.0.620
7.抛一个杯口和杯底大小不同的纸杯,落地有三种可能性:①杯口向上②杯底向上③侧面着地,则杯口向上的概率为( )
A.
B.
C.
D.只能用大量重复试验,频率估计概率的方法求得
三、解答题
8.研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n 100 200 300 500 800 1000
摸到有记号球的次数m 25 44 57 105 160 199
摸到有记号球的频率
0.25 0.22 0.19 0.21 0.20 0.20
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
四、作图题
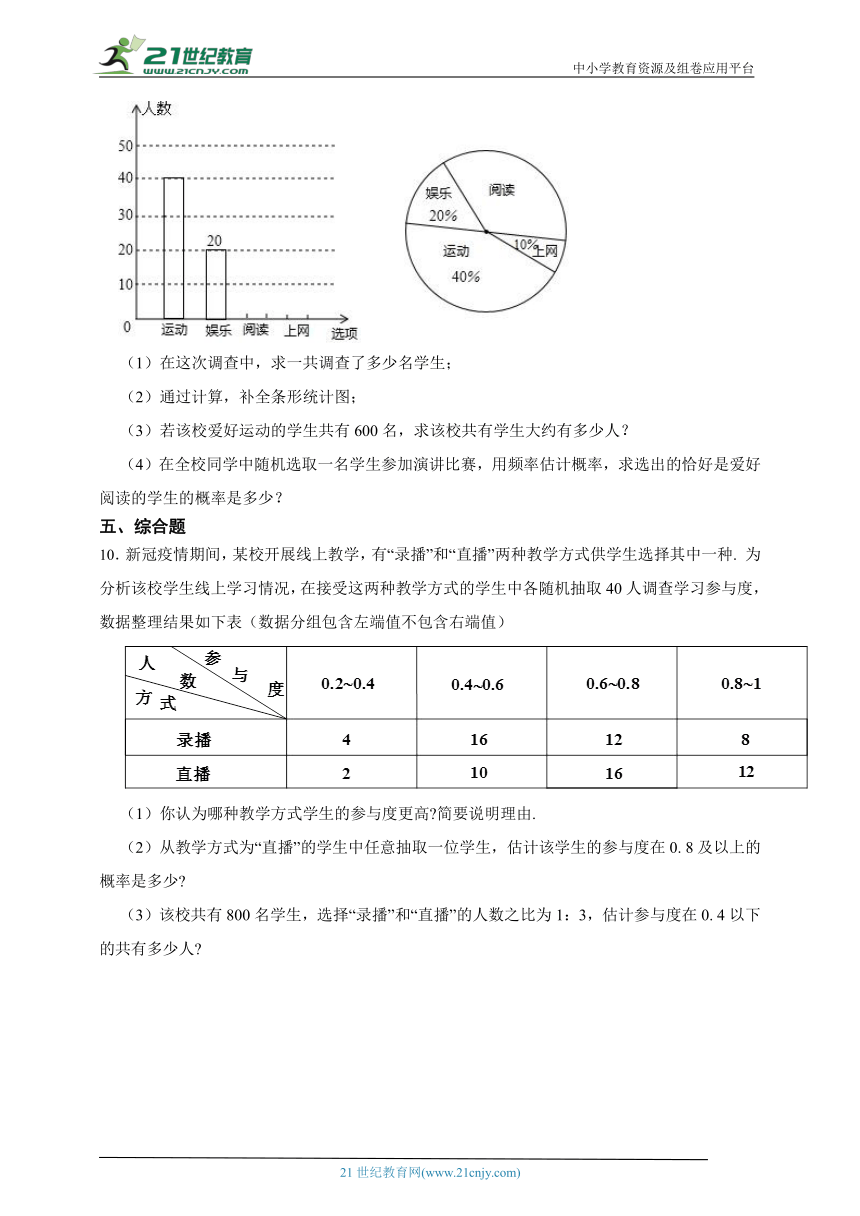
9.某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调査结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中,求一共调查了多少名学生;
(2)通过计算,补全条形统计图;
(3)若该校爱好运动的学生共有600名,求该校共有学生大约有多少人?
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,求选出的恰好是爱好阅读的学生的概率是多少?
五、综合题
10.新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种. 为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如下表(数据分组包含左端值不包含右端值)
(1)你认为哪种教学方式学生的参与度更高 简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0. 8及以上的概率是多少
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0. 4以下的共有多少人
答案解析部分
1.【答案】
【解析】【解答】解:当重复试验次数足够多时,频率逐渐稳定在0.5左右,
∴掷一枚均匀的硬币,正面朝上的概率是.
故答案为:.
【分析】根据频率估计概率的知识进行解答即可.
2.【答案】0.60;0.60;0.40;8;12
【解析】【解答】解;(1)根据表格中数据的第六行摸到白球的频率,可知当n很大时,摸到白球的频率将会接近0.60;
(2)由(1)知,当摸球的次数n很大,根据频率与概率的关系,摸到白球的实验概率近似等于摸到白球的频率,所以摸到白球的概率约为0.60,摸到黑球的概率是0.40;
(3)盒子中白球的个数约为20×0.6=12(个),
则黑球个数为:20﹣12=8(个);
故答案为:0.60;0.60;0.40;8;12.
【分析】(1)根据表格中数据估计白球的频率即可;
(2)利用频率估计概率得出答案即可;
(3)根据黑、白两种颜色的球共20个,以及摸到白球的概率求出小球个数即可.
3.【答案】C
【解析】【解答】解:设白球个数为x个,
∵摸到红色球的频率稳定在0.2左右,
∴口袋中得到红色球的概率为0.2,
∴ ,
解得:x=20,
经检验x=20是原方程的根,
故白球的个数为20个.
故答案为:C.
【分析】由摸到红球的频率稳定在0.2附近得出从口袋中摸出红色球的概率,进而求出白球个数即可.
4.【答案】D
【解析】【解答】解:∵摸到白色球的频率稳定在85%左右,
∴口袋中白色球的频率为85%,
故白球的个数为40×85%=34个,
∴口袋中红色球的个数为40-34=6个
故答案为:D.
【分析】由频数=数据总数×频率计算即可.
5.【答案】D
【解析】【解答】解:A. 连续掷2次时,正面朝上有可能出现,还有可能不出现,A判断不符合题意;
B. 连续掷100次时,正面朝上不一定会出现50次,B判断不符合题意;
C. 连续掷次时,正面朝上不一定会出现次,C判断不符合题意;
D. 当抛掷次数越大时,正面朝上的频率越稳定于0.5,符合题意,D符合题意,
故答案为:D.
【分析】利用频率估计概率的计算方法求解即可。
6.【答案】C
【解析】【解答】解:∵由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数0.600附近,
∴这名球员在罚球线上投篮一次,投中的概率为0.600.
故答案为:C.
【分析】利用频率估算概率即可得到答案。
7.【答案】D
【解析】【解答】解:∵抛一个杯口和杯底大小不同的纸杯,落地有三种可能性:①杯口向上②杯底向上③侧面着地,
∴此事件不是等可能事件,由此只能用大量重复试验,频率估计概率的方法求得.
故答案为:D.
【分析】根据已知条件:杯口和杯底大小不同的纸杯,落地有三种可能性,可知此事件不是等可能事件,由此可得答案。
8.【答案】解:(1)根据105÷500=0.21,160÷800=0.2,199÷1000≈0.2,
故摸到有记号球的概率是:0.2;
(2)根据图表可以得出摸到有记号球的概率是0.2,
故盒中共有球:=0.2,
解得:x=40,
故没有记号球有40﹣8=32个.
【解析】【分析】(1)根据图表数据进而分析得出摸到有记号球的概率;
(2)根据(1)中所求概率,即可得出盒中共有球的个数以及没有带记号的个数.
9.【答案】(1)解:爱好运动的人数为40,所占百分比为40%
∴共调查人数为:40÷40%=100
(2)解:爱好上网的人数所占百分比为10%
∴爱好上网人数为:100×10%=10,
∴爱好阅读人数为:100﹣40﹣20﹣10=30,
补全条形统计图,如图所示,
(3)解:爱好运动的学生人数所占的百分比为40%,
∴该校共有学生大约有:600÷40%=1500人;
(4)解:爱好阅读的学生人数所占的百分比30%,
∴用频率估计概率,则选出的恰好是爱好阅读的学生的概率为
【解析】【分析】(1)根据爱好运动人数的百分比,以及运动人数即可求出共调查的人数;(2)根据两幅统计图即可求出阅读的人数以及上网的人数,从而可补全图形.(3)利用样本估计总体即可估计爱好运动的学生人数.(4)根据爱好阅读的学生人数所占的百分比即可估计选出的恰好是爱好阅读的学生的概率.
10.【答案】(1)直播”教学方式学生的参与度更高;
理由:“直播”参与度在0.6以上的人数为28人,“录播”参与度在0.6以上的人数为20人,参与度在0.6以上的“直播”人数远多于“录播”人数,所以“直播”教学方式学生的参与度更高。
(2)解:12÷40=0.3=30%
答:该学生的参与度在0.8及以上的概率是30%
(3)解:录播”总学生数:800× =200(人)
“直播”总学生数:800× =600(人)
“录播”参与度在0.4以下的学生数:200× =20(人)
“直播”参与度在0.4以下的学生数:600× =30(人)
参与度在0.4以下的学生共有:20+30=50(人)
【解析】【分析】(1)根据表格数据得出两种教学方式参与度在0.6以上的人数,比较即可作出判断;(2)用表格中“直播”教学方式学生参与度在0.8以上的人数除以被调查的总人数即可估计对应概率;(3)先根据“录播”和“直播”的人数之比为1:3及该校学生总人数求出“直播”、“录播”人数,再分别乘以两种教学方式中参与度在0.4以下人数所占比例求出对应人数,再相加即可得出答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
25.3 用频率估计概率一课一练
一、填空题
1.当重复试验次数足够多时,可用频率来估计概率.历史上数学家皮尔逊(Pearson)曾在实验中掷均匀的硬币24000次,正面朝上的次数是12012次,频率约为0.5,则掷一枚均匀的硬币,正面朝上的概率是 .
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个记下颜色,再把它放回口袋中,不断重复,如表是活动进行中的一组数据统计:
摸球的次数m 100 150 200 500 800 1000
摸到白球的次数n 58 96 116 295 484 601
摸到白球的频率 0.58 0.64 0.58 0.59 0.605 0.601
(1)请估计:当n很大时,摸到白球的频率将会接近 ;
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 ;
(3)试估算口袋中黑球有 个,白球有 个.
二、单选题
3.在一个不透明的袋子里装有5个红球和若干个白球,它们除颜色外其余完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在0.2附近,则估计袋中的白球大约有( )个
A.10 B.15 C.20 D.25
4.在一个不透明的布袋中装有红色.白色玻璃球共40个,除颜色外其他完全相同,小明通过多次摸球试验后发现,其中摸到白色球的频率稳定在85%左右,则口袋中红色球可能有( ).
A.34个 B.30个 C.10个 D.6个
5.抛掷一枚质地均匀的硬币时,正面向上的概率是0.5.则下列判断正确的是( )
A.连续掷2次时,正面朝上一定会出现1次
B.连续掷100次时,正面朝上一定会出现50次
C.连续掷次时,正面朝上一定会出现次
D.当抛掷次数越大时,正面朝上的频率越稳定于0.5
6.下表记录了一名球员在罚球线上投篮的结果:
投篮次数 50 100 150 200 250 400 500 800
投中次数 28 63 87 122 148 242 301 480
投中频率 0.560 0.630 0.580 0.610 0.592 0.605 0.602 0.600
根据频率的稳定性,估计这名球员投篮一次投中的概率约是( )
A.0.560 B.0.580 C.0.600 D.0.620
7.抛一个杯口和杯底大小不同的纸杯,落地有三种可能性:①杯口向上②杯底向上③侧面着地,则杯口向上的概率为( )
A.
B.
C.
D.只能用大量重复试验,频率估计概率的方法求得
三、解答题
8.研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n 100 200 300 500 800 1000
摸到有记号球的次数m 25 44 57 105 160 199
摸到有记号球的频率
0.25 0.22 0.19 0.21 0.20 0.20
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?
四、作图题
9.某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调査结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中,求一共调查了多少名学生;
(2)通过计算,补全条形统计图;
(3)若该校爱好运动的学生共有600名,求该校共有学生大约有多少人?
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,求选出的恰好是爱好阅读的学生的概率是多少?
五、综合题
10.新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种. 为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如下表(数据分组包含左端值不包含右端值)
(1)你认为哪种教学方式学生的参与度更高 简要说明理由.
(2)从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0. 8及以上的概率是多少
(3)该校共有800名学生,选择“录播”和“直播”的人数之比为1:3,估计参与度在0. 4以下的共有多少人
答案解析部分
1.【答案】
【解析】【解答】解:当重复试验次数足够多时,频率逐渐稳定在0.5左右,
∴掷一枚均匀的硬币,正面朝上的概率是.
故答案为:.
【分析】根据频率估计概率的知识进行解答即可.
2.【答案】0.60;0.60;0.40;8;12
【解析】【解答】解;(1)根据表格中数据的第六行摸到白球的频率,可知当n很大时,摸到白球的频率将会接近0.60;
(2)由(1)知,当摸球的次数n很大,根据频率与概率的关系,摸到白球的实验概率近似等于摸到白球的频率,所以摸到白球的概率约为0.60,摸到黑球的概率是0.40;
(3)盒子中白球的个数约为20×0.6=12(个),
则黑球个数为:20﹣12=8(个);
故答案为:0.60;0.60;0.40;8;12.
【分析】(1)根据表格中数据估计白球的频率即可;
(2)利用频率估计概率得出答案即可;
(3)根据黑、白两种颜色的球共20个,以及摸到白球的概率求出小球个数即可.
3.【答案】C
【解析】【解答】解:设白球个数为x个,
∵摸到红色球的频率稳定在0.2左右,
∴口袋中得到红色球的概率为0.2,
∴ ,
解得:x=20,
经检验x=20是原方程的根,
故白球的个数为20个.
故答案为:C.
【分析】由摸到红球的频率稳定在0.2附近得出从口袋中摸出红色球的概率,进而求出白球个数即可.
4.【答案】D
【解析】【解答】解:∵摸到白色球的频率稳定在85%左右,
∴口袋中白色球的频率为85%,
故白球的个数为40×85%=34个,
∴口袋中红色球的个数为40-34=6个
故答案为:D.
【分析】由频数=数据总数×频率计算即可.
5.【答案】D
【解析】【解答】解:A. 连续掷2次时,正面朝上有可能出现,还有可能不出现,A判断不符合题意;
B. 连续掷100次时,正面朝上不一定会出现50次,B判断不符合题意;
C. 连续掷次时,正面朝上不一定会出现次,C判断不符合题意;
D. 当抛掷次数越大时,正面朝上的频率越稳定于0.5,符合题意,D符合题意,
故答案为:D.
【分析】利用频率估计概率的计算方法求解即可。
6.【答案】C
【解析】【解答】解:∵由频率分布表可知,随着投篮次数越来越大时,频率逐渐稳定到常数0.600附近,
∴这名球员在罚球线上投篮一次,投中的概率为0.600.
故答案为:C.
【分析】利用频率估算概率即可得到答案。
7.【答案】D
【解析】【解答】解:∵抛一个杯口和杯底大小不同的纸杯,落地有三种可能性:①杯口向上②杯底向上③侧面着地,
∴此事件不是等可能事件,由此只能用大量重复试验,频率估计概率的方法求得.
故答案为:D.
【分析】根据已知条件:杯口和杯底大小不同的纸杯,落地有三种可能性,可知此事件不是等可能事件,由此可得答案。
8.【答案】解:(1)根据105÷500=0.21,160÷800=0.2,199÷1000≈0.2,
故摸到有记号球的概率是:0.2;
(2)根据图表可以得出摸到有记号球的概率是0.2,
故盒中共有球:=0.2,
解得:x=40,
故没有记号球有40﹣8=32个.
【解析】【分析】(1)根据图表数据进而分析得出摸到有记号球的概率;
(2)根据(1)中所求概率,即可得出盒中共有球的个数以及没有带记号的个数.
9.【答案】(1)解:爱好运动的人数为40,所占百分比为40%
∴共调查人数为:40÷40%=100
(2)解:爱好上网的人数所占百分比为10%
∴爱好上网人数为:100×10%=10,
∴爱好阅读人数为:100﹣40﹣20﹣10=30,
补全条形统计图,如图所示,
(3)解:爱好运动的学生人数所占的百分比为40%,
∴该校共有学生大约有:600÷40%=1500人;
(4)解:爱好阅读的学生人数所占的百分比30%,
∴用频率估计概率,则选出的恰好是爱好阅读的学生的概率为
【解析】【分析】(1)根据爱好运动人数的百分比,以及运动人数即可求出共调查的人数;(2)根据两幅统计图即可求出阅读的人数以及上网的人数,从而可补全图形.(3)利用样本估计总体即可估计爱好运动的学生人数.(4)根据爱好阅读的学生人数所占的百分比即可估计选出的恰好是爱好阅读的学生的概率.
10.【答案】(1)直播”教学方式学生的参与度更高;
理由:“直播”参与度在0.6以上的人数为28人,“录播”参与度在0.6以上的人数为20人,参与度在0.6以上的“直播”人数远多于“录播”人数,所以“直播”教学方式学生的参与度更高。
(2)解:12÷40=0.3=30%
答:该学生的参与度在0.8及以上的概率是30%
(3)解:录播”总学生数:800× =200(人)
“直播”总学生数:800× =600(人)
“录播”参与度在0.4以下的学生数:200× =20(人)
“直播”参与度在0.4以下的学生数:600× =30(人)
参与度在0.4以下的学生共有:20+30=50(人)
【解析】【分析】(1)根据表格数据得出两种教学方式参与度在0.6以上的人数,比较即可作出判断;(2)用表格中“直播”教学方式学生参与度在0.8以上的人数除以被调查的总人数即可估计对应概率;(3)先根据“录播”和“直播”的人数之比为1:3及该校学生总人数求出“直播”、“录播”人数,再分别乘以两种教学方式中参与度在0.4以下人数所占比例求出对应人数,再相加即可得出答案.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
