人教版四年级下册数学 《三角形的内角和》(课件)(共22张PPT)
文档属性
| 名称 | 人教版四年级下册数学 《三角形的内角和》(课件)(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 22:51:32 | ||
图片预览






文档简介
(共22张PPT)
第五单元 三角形的内角和
人教版四年级数学下册
困惑一:
关于三角形内角和,你知道了什么?
01
开门见山,揭示课题
三角形的内角是什么?
三角形的内角和是什么?
三角形
2
3
1
一个三角形中,里面的三个角就是三角形的内角。
三角形
2
3
1
三角形三个内角的度数之和叫做三角形的内角和。
即:∠1+∠2+∠3=三角形的内角和
三角形的内角和
∟
∟
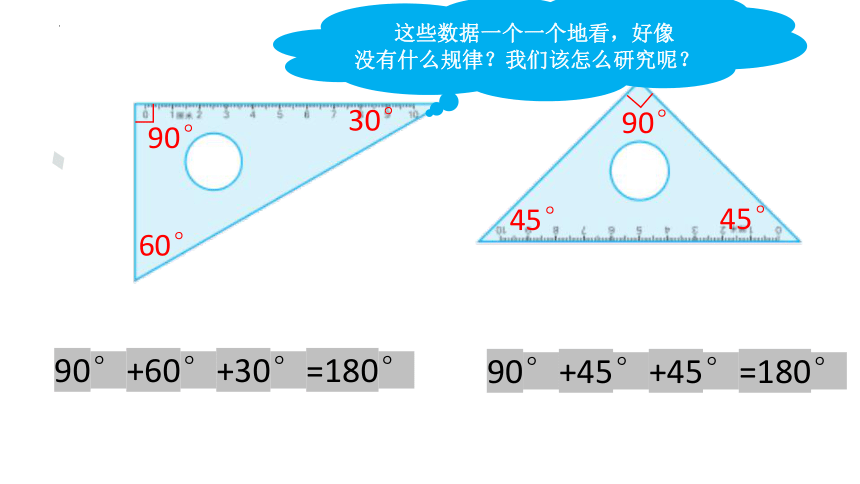
90°
60°
30°
45°
45°
90°
90°+60°+30°=180°
90°+45°+45°=180°
这些数据一个一个地看,好像没有什么规律?我们该怎么研究呢?
困惑二:
三角尺内角和是180°,是不是所有的三角形内角和都是180°呢?
02
动手操作,探索新知
许多数学问题都可以通过举例子的方法来证明,这就是由中国科学家洪加威、张景中等人提出的例证法。
张景中
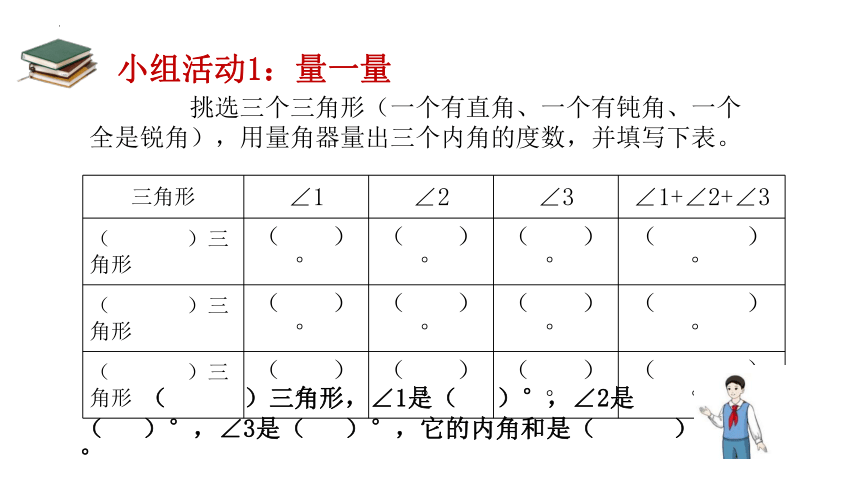
三角形 ∠1 ∠2 ∠3 ∠1+∠2+∠3
( )三角形 ( )° ( )° ( )° ( )°
( )三角形 ( )° ( )° ( )° ( )°
( )三角形 ( )° ( )° ( )° ( )°
挑选三个三角形(一个有直角、一个有钝角、一个全是锐角),用量角器量出三个内角的度数,并填写下表。
( )三角形,∠1是( )°,∠2是( )°,∠3是( )°,它的内角和是( )°
小组活动1:量一量
2
1
3
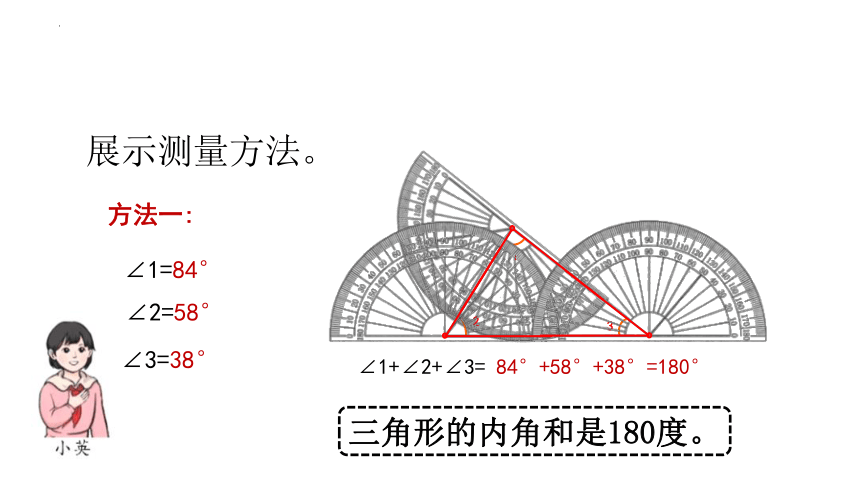
∠1+∠2+∠3= 84°+58°+38°=180°
方法一:
∠1=84°
∠2=58°
∠3=38°
三角形的内角和是180度。
展示测量方法。
小组活动2:按照下面的方法折一折,你发现了什么?
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
方法二:
三角形的内角和是180度。
方法二:
2
1
1
3
3
锐角三角形
2
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
方法二:
1
1
2
2
3
3
直角三角形
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
方法三:
3
3
2
1
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
小组活动3:将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
新究探知
困惑三:
同学们研究明白了吗?我们一起来了解法国数学家帕斯卡验证三角形内角和的过程吧!
03
帕斯卡:法国的数学家、物理学家,为人类创造了无数的奇迹,早在300年前这位法国著名的科学家就已经发现了:
任何三角形的内角和都是180°。
他当时年仅12岁。
360 ÷2=180
。
。
……
180 ×2
。
。
-180 =180
。
直角三角形
质疑问难,寻求突破
锐角三角形
钝角三角形
转 化
三角形的内角和是180度。
长 方 形
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三角形的内角和相等,都是180°
?
巩固应用,内化提升
1.“兄弟”的争吵。
2.说说你的做法?
方法一:75°+40°=115°
180°-115°=65°
方法二:
180°-75°-40°=65°
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
三角
三角
360
180
180
90 °× 4 = 360°
3.用一张正方形纸折一折,填一填。
4.把下面这个三角形沿着虚线剪成两个小三角形,每个三角形的内角和是多少度?
解答:因为三角形的内角和是180°,所以我们把这个三角形沿虚线剪成两个小三角形后,每个三角形的内角和都是180°。
三角形的内角和是180度。
量算法
折拼法
剪拼法
三角形的内角和
有多种方法可以求证三角形的内角和
回顾梳理,概括提升
你能利用今天所学的知识想办法知道四边形、五边形和六边形等的内角和吗?
课后思考
内角和180°
内角和 ?
内角和 ?
内角和 ?
三角形
四边形
五边形
六边形
第五单元 三角形的内角和
人教版四年级数学下册
困惑一:
关于三角形内角和,你知道了什么?
01
开门见山,揭示课题
三角形的内角是什么?
三角形的内角和是什么?
三角形
2
3
1
一个三角形中,里面的三个角就是三角形的内角。
三角形
2
3
1
三角形三个内角的度数之和叫做三角形的内角和。
即:∠1+∠2+∠3=三角形的内角和
三角形的内角和
∟
∟
90°
60°
30°
45°
45°
90°
90°+60°+30°=180°
90°+45°+45°=180°
这些数据一个一个地看,好像没有什么规律?我们该怎么研究呢?
困惑二:
三角尺内角和是180°,是不是所有的三角形内角和都是180°呢?
02
动手操作,探索新知
许多数学问题都可以通过举例子的方法来证明,这就是由中国科学家洪加威、张景中等人提出的例证法。
张景中
三角形 ∠1 ∠2 ∠3 ∠1+∠2+∠3
( )三角形 ( )° ( )° ( )° ( )°
( )三角形 ( )° ( )° ( )° ( )°
( )三角形 ( )° ( )° ( )° ( )°
挑选三个三角形(一个有直角、一个有钝角、一个全是锐角),用量角器量出三个内角的度数,并填写下表。
( )三角形,∠1是( )°,∠2是( )°,∠3是( )°,它的内角和是( )°
小组活动1:量一量
2
1
3
∠1+∠2+∠3= 84°+58°+38°=180°
方法一:
∠1=84°
∠2=58°
∠3=38°
三角形的内角和是180度。
展示测量方法。
小组活动2:按照下面的方法折一折,你发现了什么?
1
2
2
3
3
钝角三角形
1
∠1+∠2+∠3
=
平角
=180°
方法二:
三角形的内角和是180度。
方法二:
2
1
1
3
3
锐角三角形
2
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
方法二:
1
1
2
2
3
3
直角三角形
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
方法三:
3
3
2
1
三角形的内角和是180度。
∠1+∠2+∠3
=
平角
=180°
小组活动3:将三角形三个内角分别剪下来拼在一起,你发现了什么?(注:剪之前标注好要拼的角哦!)
新究探知
困惑三:
同学们研究明白了吗?我们一起来了解法国数学家帕斯卡验证三角形内角和的过程吧!
03
帕斯卡:法国的数学家、物理学家,为人类创造了无数的奇迹,早在300年前这位法国著名的科学家就已经发现了:
任何三角形的内角和都是180°。
他当时年仅12岁。
360 ÷2=180
。
。
……
180 ×2
。
。
-180 =180
。
直角三角形
质疑问难,寻求突破
锐角三角形
钝角三角形
转 化
三角形的内角和是180度。
长 方 形
我有一个钝角,我的内角和是最大的!
我的个头最大,我的内角和最大!
我的三个角都是锐角,我的内角和最小吗?
三角形的内角和相等,都是180°
?
巩固应用,内化提升
1.“兄弟”的争吵。
2.说说你的做法?
方法一:75°+40°=115°
180°-115°=65°
方法二:
180°-75°-40°=65°
正方形
( )形
( )形
内角和( )°
内角和( )°
内角和( )°
三角
三角
360
180
180
90 °× 4 = 360°
3.用一张正方形纸折一折,填一填。
4.把下面这个三角形沿着虚线剪成两个小三角形,每个三角形的内角和是多少度?
解答:因为三角形的内角和是180°,所以我们把这个三角形沿虚线剪成两个小三角形后,每个三角形的内角和都是180°。
三角形的内角和是180度。
量算法
折拼法
剪拼法
三角形的内角和
有多种方法可以求证三角形的内角和
回顾梳理,概括提升
你能利用今天所学的知识想办法知道四边形、五边形和六边形等的内角和吗?
课后思考
内角和180°
内角和 ?
内角和 ?
内角和 ?
三角形
四边形
五边形
六边形
