人教版六年级下册数学第5单元《鸽巢问题》(课件)(共42张PPT)
文档属性
| 名称 | 人教版六年级下册数学第5单元《鸽巢问题》(课件)(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-25 23:09:22 | ||
图片预览



文档简介
(共42张PPT)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
鸽巢问题
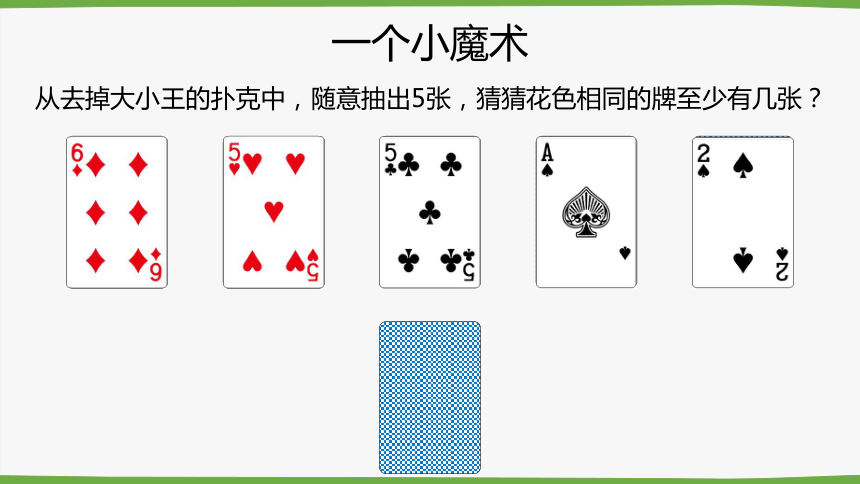
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
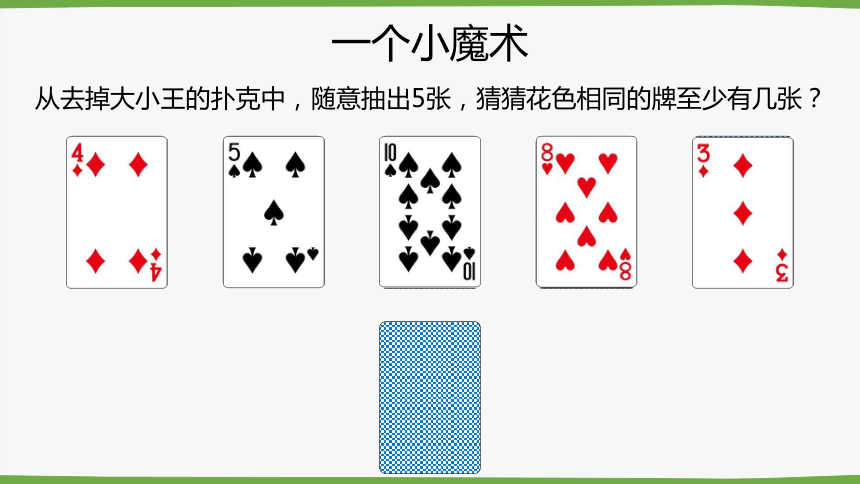
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
抢凳子游戏
1.老师宣布开始,参与的同学就围着凳子转圈,老师喊“停”的时候,每个人都必须坐在凳子上。
2.请同学们仔细观察,你将会发现一个有趣的情景。
游戏说明
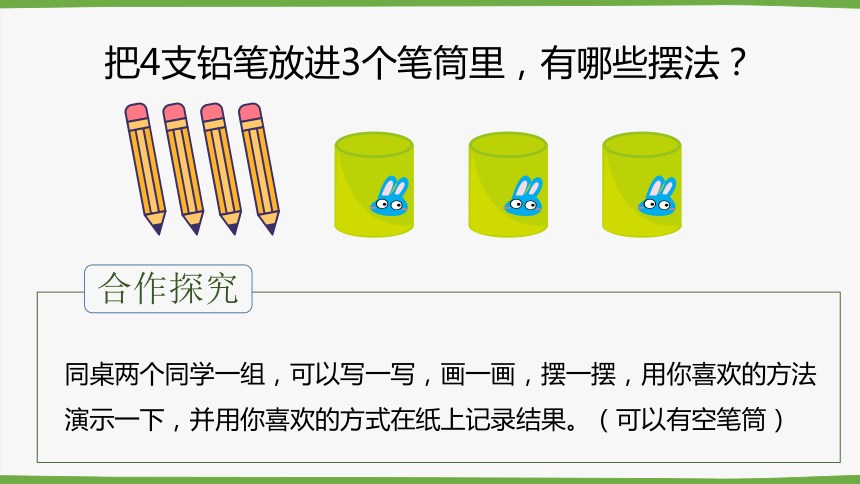
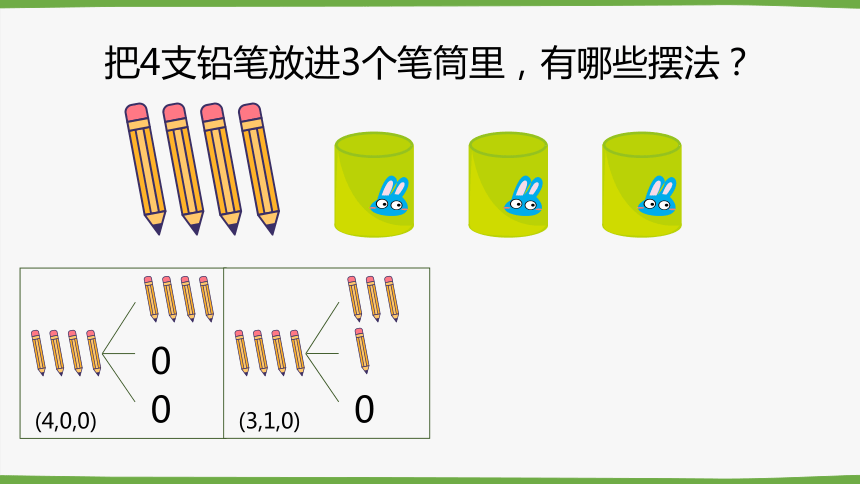
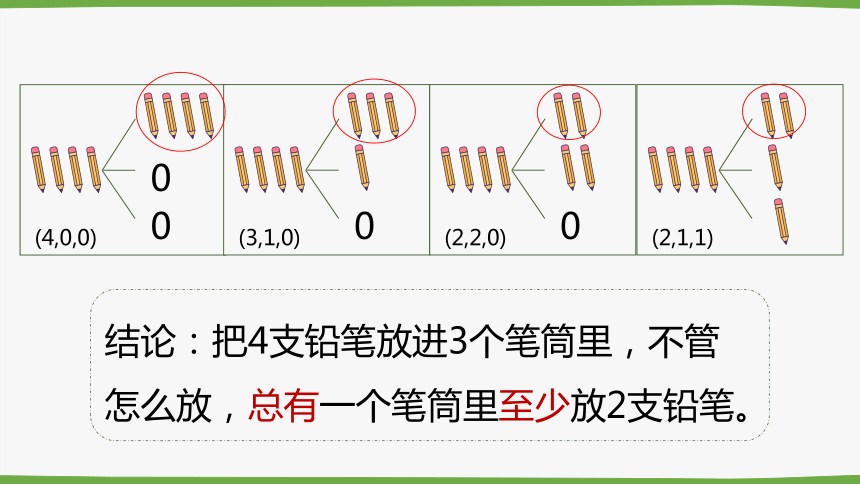
把4支铅笔放进3个笔筒里,有哪些摆法?
同桌两个同学一组,可以写一写,画一画,摆一摆,用你喜欢的方法演示一下,并用你喜欢的方式在纸上记录结果。(可以有空笔筒)
合作探究
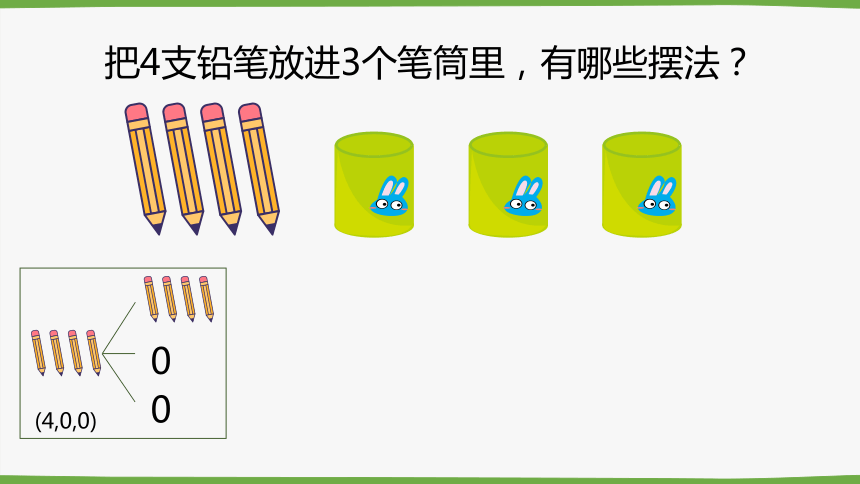
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
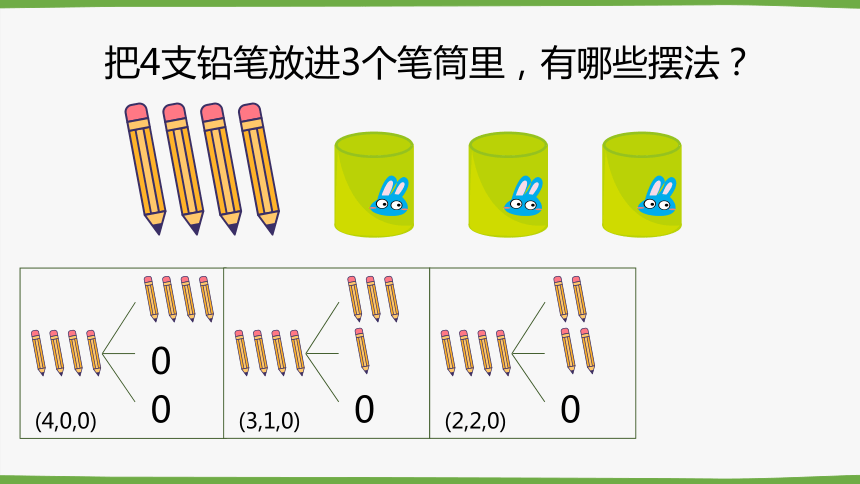
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
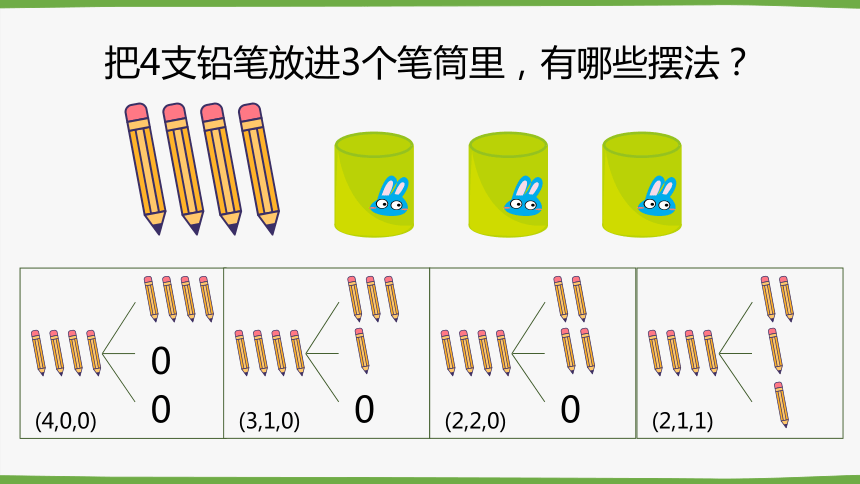
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
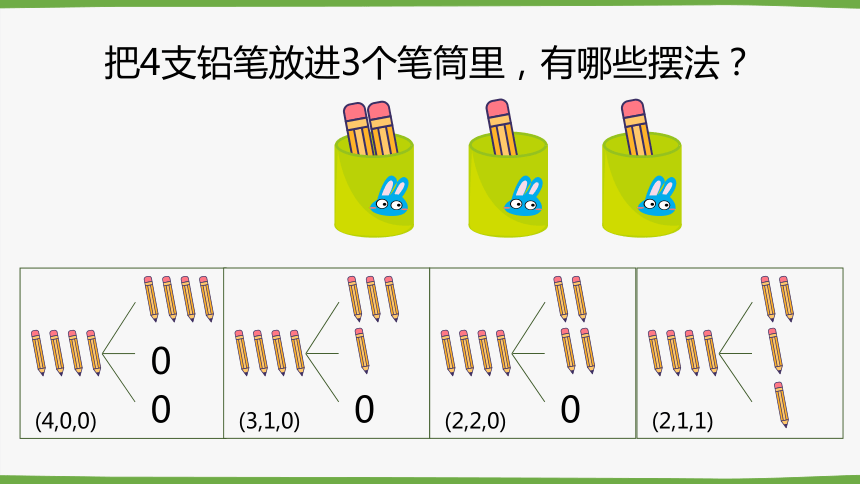
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
结论:把4支铅笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放2支铅笔。
把4支铅笔放进3个笔筒里,怎样可得知总有一个笔筒至少放几支笔?
平均分
4÷3=1(支)······1(支)
1+1=2(支)
【想一想】把5支铅笔放进4个笔筒里,总有一个笔筒至少放几支笔?为什么?
5÷4=1(支)······1(支)
1+1=2(支)
【思考】
铅笔 放进 笔筒
总有一个笔筒至少放几支笔
4
3
4÷3=1······1
1+1=2
5
4
5÷4=1······1
1+1=2
6
5
6÷5=1······1
1+1=2
7
6
7÷6=1······1
1+1=2
n+1
n
(n+1)÷n=1······1
1+1=2
······
······
······
······
抽屉原理
把n+1 任意放进n个 里(n是非0自然数),总有1个 至少放进了2 。
支铅笔
笔筒
笔筒
支铅笔
抽屉原理
把n+1 任意放进n个 里(n是非0自然数),总有1个 至少放进了2 。
抽屉
抽屉
个物体
个物体
德国 数学家
狄里克雷
(1805.2.13.~1859.5.5.)
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。
抽屉原理有两个经典案例:一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
知识拓展
6只鸽子飞回5个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
6÷5=1(只)······1(只)
1+1=2(只)
5只鸽子飞回3个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
5÷3=1(只)······2(只)
1+1=2(只)
7只鸽子飞回5个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
7÷5=1(只)······2(只)
1+1=2(只)
抽屉原理
把n+1或多于n+1(不到n的2倍)个物体任意放进n个抽屉里(n是非0自然数),总有1个抽屉至少放进了2个物体。
把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进3本书。为什么?
平均分
7÷3=2(本)······1(本)
2+1=3(本)
把8本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
8÷3=2(本)······2(本)
2+1=3(本)
答:总有一个抽屉至少放进3本书。
把9本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
9÷3=3(本)
答:总有一个抽屉至少放进3本书。
把10本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
10÷3=3(本)······1(本)
3+1=4(本)
答:总有一个抽屉至少放进4本书。
【思考】
书本 放进 抽屉
总有一个抽屉至少放几本书
7
3
7÷3=2······1
2+1=3
8
3
8÷3=2······2
2+1=3
9
3
9÷3=3
3
10
3
10÷3=3······1
3+1=4
······
······
······
······
你有什么发现?
—把a个物体放入n个抽屉,
如果 a÷n=b······c (c≠0),
那么总有一个抽屉至少可以放入b+1个物体;
如果 a÷n=b,
那么总有一个抽屉至少可以放入b个物体。
计算至少数的小技巧
解决“鸽巢问题”的关键是找准哪是物体,哪是抽屉。
总有一个抽屉至
少有( )个物体
物体
抽屉
物体个数 ÷ 抽屉个数
有余数
无余数
商+1
商
【练习1】11只鸽子飞进4个笼子,总有一个笼子至少飞进多少只鸽子?
11÷4=2(只)······1(只)
2+1=3(只)
答:总有一个笼子至少飞进3只鸽子。
物体:
11只鸽子
抽屉:
4个笼子
【练习2】随意找24位老师,他们中至少有几位属相相同?
24÷12=2(位)
答:他们中至少有2位属相相同。
物体:
24位老师
抽屉:
12生肖
【练习3】从任意6双手套中任取7只,其中至少有2只恰好为一双手套吗 ?
7÷6=1(只)······1(只)
1+1=2(只)
答:至少有2只恰好为一双手套。
物体:
7只手套
抽屉:
6双
【练习4】用三种颜色给正方体的各面涂色(每面只涂一种颜色),那么至少有几个面颜色相同?
物体:
6个面
抽屉:
3种颜色
6÷3=2(个)
答:至少有2个面颜色相同。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
A与B、C、D、E、F之间要画5条线,则
5÷2=2······1
2+1=3
这5条线中至少有3条相同,假设3条相同的是红线。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
B、C、D三人之间共要画3条线,则
3÷2=2······1
1+1=2
这3条线中至少有2条相同,假设2条相同的是绿线。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
A、B、D三人之间构成了一个红色三角形,这也就证明了在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人
箱子里有同样大小的红、蓝、黄、绿、紫球各4个,要想摸出的球一定有2个同色的,至少要摸几个球?
颜色 保证同色 至少摸几个球
2种 2个 3个
3种 2个 4个
4种 2个 5个
5种 2个 ?个
快乐时光
这是一个智慧游戏,赶紧用你的智慧来赢取属于你的荣誉。你准备好了吗?
希望小学篮球兴趣小组的25名同学中,最大的12岁,最小的6岁,至少从中挑选几名同学,就一定能找到两名同学年龄相同?
6
7
8
9
8
不对喔!
不对喔!
不对喔!
不对喔!
11
袋子里有50个编有号码的大小相同的小球,其中编号为1,2,3,4,5的各10个。至少要摸出多少个才能保证其中至少有2个号码相同的小球?
4
5
6
7
8
不对喔!
不对喔!
不对喔!
不对喔!
3
有红、绿、蓝三种颜色的筷子各8根,混杂在一起。黑暗中想从这些筷子中取出两双筷子,问至少要取多少根才能保证达到要求?(同色的两根算一双)
9
8
7
6
5
不对喔!
不对喔!
不对喔!
不对喔!
祝贺你(xx小组)获得冠军!
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
鸽巢问题
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
一个小魔术
从去掉大小王的扑克中,随意抽出5张,猜猜花色相同的牌至少有几张?
抢凳子游戏
1.老师宣布开始,参与的同学就围着凳子转圈,老师喊“停”的时候,每个人都必须坐在凳子上。
2.请同学们仔细观察,你将会发现一个有趣的情景。
游戏说明
把4支铅笔放进3个笔筒里,有哪些摆法?
同桌两个同学一组,可以写一写,画一画,摆一摆,用你喜欢的方法演示一下,并用你喜欢的方式在纸上记录结果。(可以有空笔筒)
合作探究
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
把4支铅笔放进3个笔筒里,有哪些摆法?
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
0
0
(4,0,0)
0
(3,1,0)
0
(2,2,0)
(2,1,1)
结论:把4支铅笔放进3个笔筒里,不管怎么放,总有一个笔筒里至少放2支铅笔。
把4支铅笔放进3个笔筒里,怎样可得知总有一个笔筒至少放几支笔?
平均分
4÷3=1(支)······1(支)
1+1=2(支)
【想一想】把5支铅笔放进4个笔筒里,总有一个笔筒至少放几支笔?为什么?
5÷4=1(支)······1(支)
1+1=2(支)
【思考】
铅笔 放进 笔筒
总有一个笔筒至少放几支笔
4
3
4÷3=1······1
1+1=2
5
4
5÷4=1······1
1+1=2
6
5
6÷5=1······1
1+1=2
7
6
7÷6=1······1
1+1=2
n+1
n
(n+1)÷n=1······1
1+1=2
······
······
······
······
抽屉原理
把n+1 任意放进n个 里(n是非0自然数),总有1个 至少放进了2 。
支铅笔
笔筒
笔筒
支铅笔
抽屉原理
把n+1 任意放进n个 里(n是非0自然数),总有1个 至少放进了2 。
抽屉
抽屉
个物体
个物体
德国 数学家
狄里克雷
(1805.2.13.~1859.5.5.)
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。
抽屉原理有两个经典案例:一个是把10个苹果放进9个抽屉里,总有一个抽屉里至少放了2个苹果,所以这个原理又称“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有一个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
知识拓展
6只鸽子飞回5个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
6÷5=1(只)······1(只)
1+1=2(只)
5只鸽子飞回3个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
5÷3=1(只)······2(只)
1+1=2(只)
7只鸽子飞回5个鸽笼,总有一个鸽笼至少飞进2只鸽子。为什么?
平均分
7÷5=1(只)······2(只)
1+1=2(只)
抽屉原理
把n+1或多于n+1(不到n的2倍)个物体任意放进n个抽屉里(n是非0自然数),总有1个抽屉至少放进了2个物体。
把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进3本书。为什么?
平均分
7÷3=2(本)······1(本)
2+1=3(本)
把8本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
8÷3=2(本)······2(本)
2+1=3(本)
答:总有一个抽屉至少放进3本书。
把9本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
9÷3=3(本)
答:总有一个抽屉至少放进3本书。
把10本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进多少本书?
平均分
10÷3=3(本)······1(本)
3+1=4(本)
答:总有一个抽屉至少放进4本书。
【思考】
书本 放进 抽屉
总有一个抽屉至少放几本书
7
3
7÷3=2······1
2+1=3
8
3
8÷3=2······2
2+1=3
9
3
9÷3=3
3
10
3
10÷3=3······1
3+1=4
······
······
······
······
你有什么发现?
—把a个物体放入n个抽屉,
如果 a÷n=b······c (c≠0),
那么总有一个抽屉至少可以放入b+1个物体;
如果 a÷n=b,
那么总有一个抽屉至少可以放入b个物体。
计算至少数的小技巧
解决“鸽巢问题”的关键是找准哪是物体,哪是抽屉。
总有一个抽屉至
少有( )个物体
物体
抽屉
物体个数 ÷ 抽屉个数
有余数
无余数
商+1
商
【练习1】11只鸽子飞进4个笼子,总有一个笼子至少飞进多少只鸽子?
11÷4=2(只)······1(只)
2+1=3(只)
答:总有一个笼子至少飞进3只鸽子。
物体:
11只鸽子
抽屉:
4个笼子
【练习2】随意找24位老师,他们中至少有几位属相相同?
24÷12=2(位)
答:他们中至少有2位属相相同。
物体:
24位老师
抽屉:
12生肖
【练习3】从任意6双手套中任取7只,其中至少有2只恰好为一双手套吗 ?
7÷6=1(只)······1(只)
1+1=2(只)
答:至少有2只恰好为一双手套。
物体:
7只手套
抽屉:
6双
【练习4】用三种颜色给正方体的各面涂色(每面只涂一种颜色),那么至少有几个面颜色相同?
物体:
6个面
抽屉:
3种颜色
6÷3=2(个)
答:至少有2个面颜色相同。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
A与B、C、D、E、F之间要画5条线,则
5÷2=2······1
2+1=3
这5条线中至少有3条相同,假设3条相同的是红线。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
B、C、D三人之间共要画3条线,则
3÷2=2······1
1+1=2
这3条线中至少有2条相同,假设2条相同的是绿线。
聚会难题
1947年的匈牙利全国数学竞赛上有这样一道题:
在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人。
此题曾经难倒很多数学家。
A
B
C
D
E
F
用字母A~F分别表示6个人。
相识画:
不相识画:
A、B、D三人之间构成了一个红色三角形,这也就证明了在任意6个人的集会上,一定可以找到3个互相认识的人或者3个互相不认识的人
箱子里有同样大小的红、蓝、黄、绿、紫球各4个,要想摸出的球一定有2个同色的,至少要摸几个球?
颜色 保证同色 至少摸几个球
2种 2个 3个
3种 2个 4个
4种 2个 5个
5种 2个 ?个
快乐时光
这是一个智慧游戏,赶紧用你的智慧来赢取属于你的荣誉。你准备好了吗?
希望小学篮球兴趣小组的25名同学中,最大的12岁,最小的6岁,至少从中挑选几名同学,就一定能找到两名同学年龄相同?
6
7
8
9
8
不对喔!
不对喔!
不对喔!
不对喔!
11
袋子里有50个编有号码的大小相同的小球,其中编号为1,2,3,4,5的各10个。至少要摸出多少个才能保证其中至少有2个号码相同的小球?
4
5
6
7
8
不对喔!
不对喔!
不对喔!
不对喔!
3
有红、绿、蓝三种颜色的筷子各8根,混杂在一起。黑暗中想从这些筷子中取出两双筷子,问至少要取多少根才能保证达到要求?(同色的两根算一双)
9
8
7
6
5
不对喔!
不对喔!
不对喔!
不对喔!
祝贺你(xx小组)获得冠军!
