12.2 三角形全等的判定同步练习(无答案)人教版八年级数学上册
文档属性
| 名称 | 12.2 三角形全等的判定同步练习(无答案)人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 288.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 10:32:23 | ||
图片预览

文档简介
人教版八年级上12.2 三角形全等的判定
一、选择题
1. 如图,小明不慎将一块三角形的玻璃打碎为三块,他想只带其中一块碎片到商店去配一块与原来一样的三角形玻璃,那么他应该带去的一块是( )
A.① B.② C.③ D.都可以
2. 下列命题的逆命题是真命题的是( ).
A.全等三角形的对应边相等 B.全等三角形的对应角相等
C.如果两个数相等,那么这两个数的绝对值相等 D.无理数是无限小数
3. 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,若测量得,则工件内槽宽AB为( )
A. B. C. D.
4. 如图所示:已知,,添加下列条件不能判定与全等的是:( )
A. B. C. D.
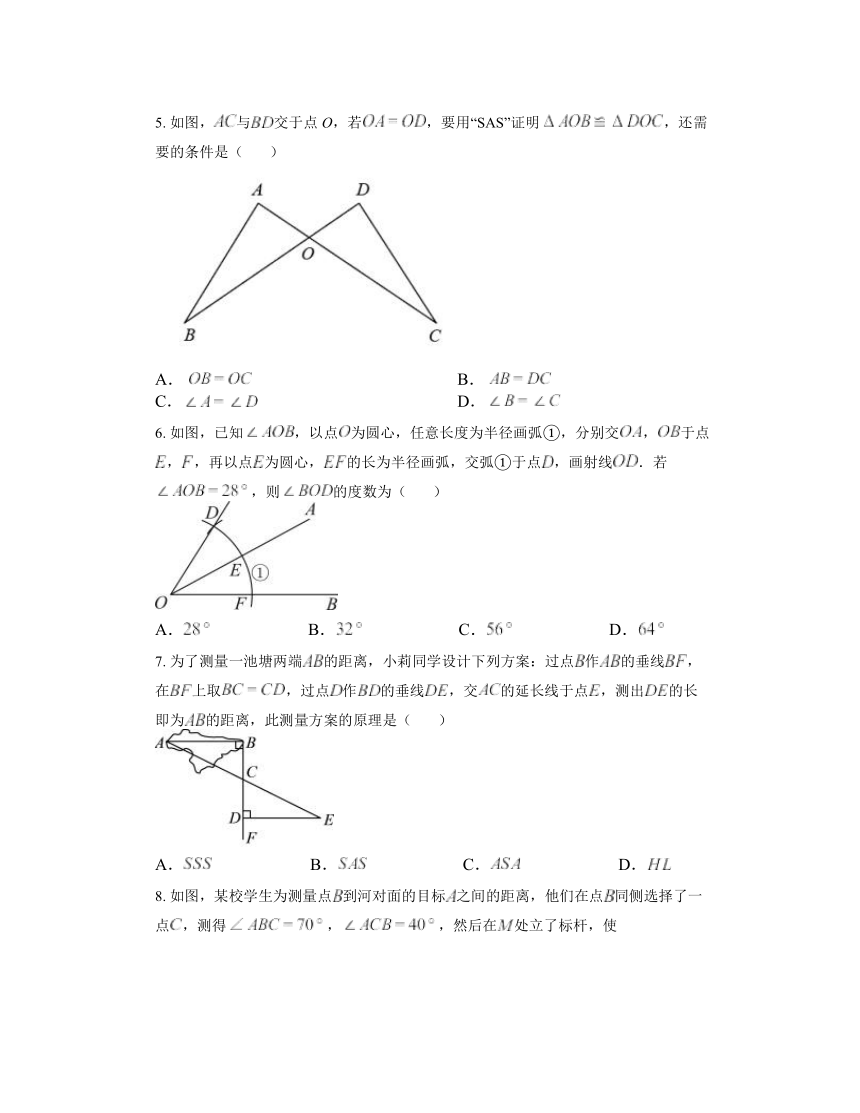
5. 如图,与交于点O,若,要用“SAS”证明,还需要的条件是( )
A. B.
C. D.
6. 如图,已知,以点为圆心,任意长度为半径画弧①,分别交,于点,,再以点为圆心,的长为半径画弧,交弧①于点,画射线.若,则的度数为( )
A. B. C. D.
7. 为了测量一池塘两端的距离,小莉同学设计下列方案:过点作的垂线,在上取,过点作的垂线,交的延长线于点,测出的长即为的距离,此测量方案的原理是( )
A. B. C. D.
8. 如图,某校学生为测量点到河对面的目标之间的距离,他们在点同侧选择了一点,测得,,然后在处立了标杆,使,为了测量,之间的距离,他们应该( )
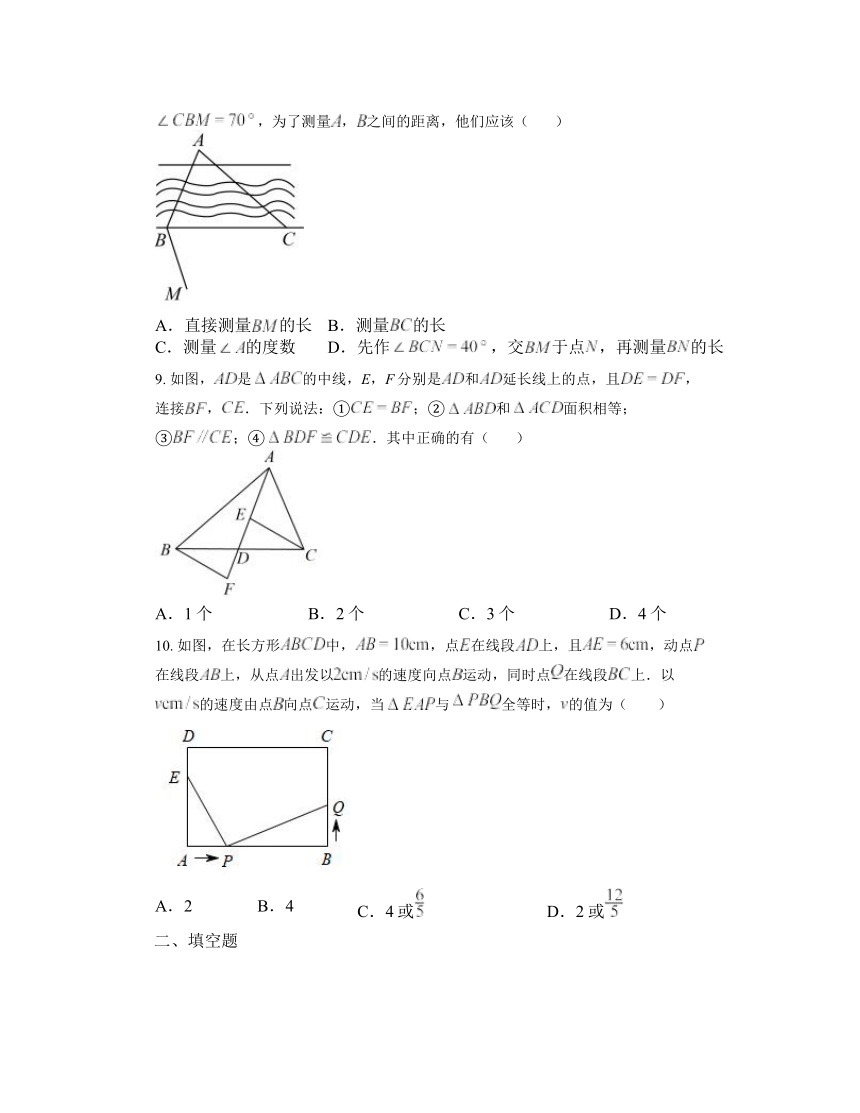
A.直接测量的长 B.测量的长
C.测量的度数 D.先作,交于点,再测量的长
9. 如图,是的中线,E,F分别是和延长线上的点,且,连接,.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10. 如图,在长方形中,,点在线段上,且,动点在线段上,从点出发以的速度向点运动,同时点在线段上.以的速度由点向点运动,当与全等时,的值为( )
A.2 B.4 C.4或 D.2或
二、填空题
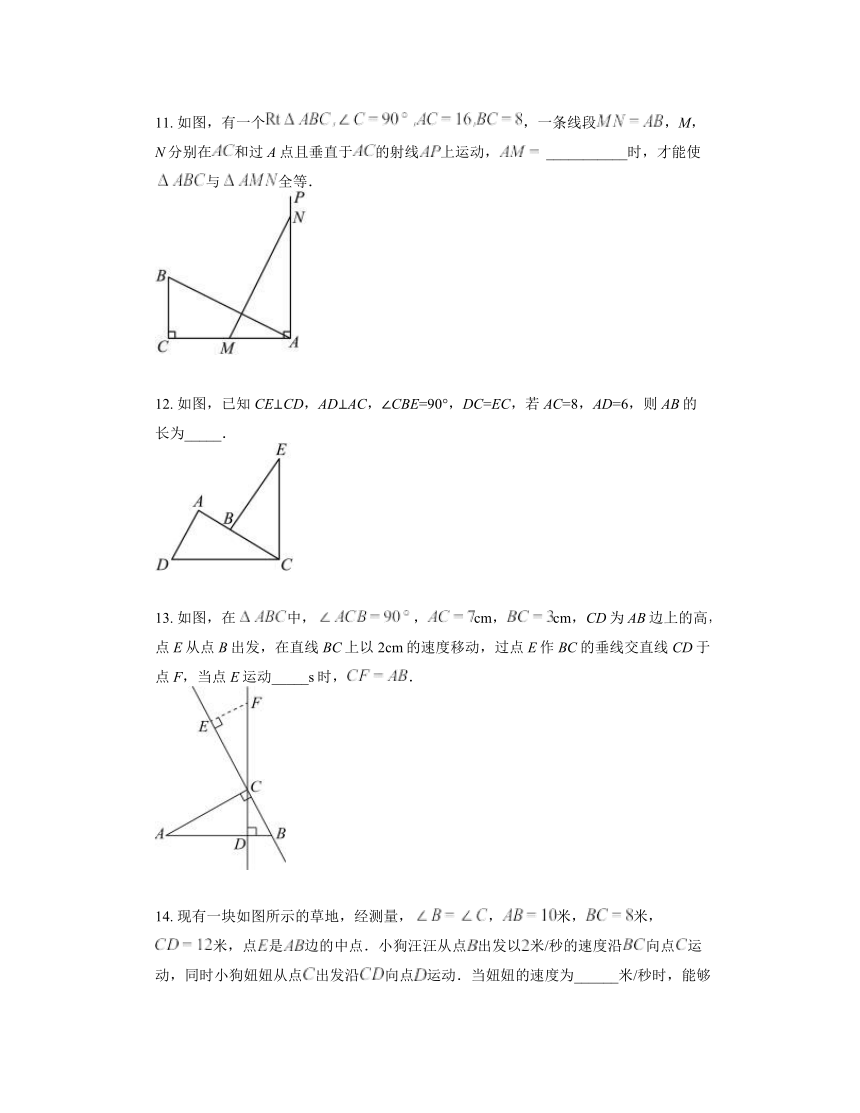
11. 如图,有一个,一条线段,M,N分别在和过A点且垂直于的射线上运动, ___________时,才能使与全等.
12. 如图,已知CE⊥CD,AD⊥AC,∠CBE=90°,DC=EC,若AC=8,AD=6,则AB的长为_____.
13. 如图,在中,,cm,cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动_____s时,.
14. 现有一块如图所示的草地,经测量,,米,米,米,点是边的中点.小狗汪汪从点出发以米/秒的速度沿向点运动,同时小狗妞妞从点出发沿向点运动.当妞妞的速度为______米/秒时,能够在某一时刻使与全等.
三、解答题
15. 如图,点A,D,B,E在同一直线上,. 求证:.
16. 尺规作图:已知:,求作:,使得.(保留作图痕迹,不写作法)
17. 已知:如图,,,.求证:.
18. 如图,在四边形中,,连接,点E在上,连接,若,.
(1)求证:.
(2)若,求的度数.
19. (1)方法学习:数学兴趣小组活动时,张老师提出了如下问题:如图1,在中,,,求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图2),
①延长到M,使得
②连接,通过三角形全等把、、转化在中;
③利用三角形的三边关系可得的取值范围为,从而得到的取值范围是 ;
方法总结:上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
(2)请你写出图2中与的数量关系和位置关系,并加以证明.
(3)深入思考:如图3,是的中线,,,,请直接利用(2)的结论,试判断线段与的数量关系,并加以证明.
一、选择题
1. 如图,小明不慎将一块三角形的玻璃打碎为三块,他想只带其中一块碎片到商店去配一块与原来一样的三角形玻璃,那么他应该带去的一块是( )
A.① B.② C.③ D.都可以
2. 下列命题的逆命题是真命题的是( ).
A.全等三角形的对应边相等 B.全等三角形的对应角相等
C.如果两个数相等,那么这两个数的绝对值相等 D.无理数是无限小数
3. 如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).在图中,若测量得,则工件内槽宽AB为( )
A. B. C. D.
4. 如图所示:已知,,添加下列条件不能判定与全等的是:( )
A. B. C. D.
5. 如图,与交于点O,若,要用“SAS”证明,还需要的条件是( )
A. B.
C. D.
6. 如图,已知,以点为圆心,任意长度为半径画弧①,分别交,于点,,再以点为圆心,的长为半径画弧,交弧①于点,画射线.若,则的度数为( )
A. B. C. D.
7. 为了测量一池塘两端的距离,小莉同学设计下列方案:过点作的垂线,在上取,过点作的垂线,交的延长线于点,测出的长即为的距离,此测量方案的原理是( )
A. B. C. D.
8. 如图,某校学生为测量点到河对面的目标之间的距离,他们在点同侧选择了一点,测得,,然后在处立了标杆,使,为了测量,之间的距离,他们应该( )
A.直接测量的长 B.测量的长
C.测量的度数 D.先作,交于点,再测量的长
9. 如图,是的中线,E,F分别是和延长线上的点,且,连接,.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10. 如图,在长方形中,,点在线段上,且,动点在线段上,从点出发以的速度向点运动,同时点在线段上.以的速度由点向点运动,当与全等时,的值为( )
A.2 B.4 C.4或 D.2或
二、填空题
11. 如图,有一个,一条线段,M,N分别在和过A点且垂直于的射线上运动, ___________时,才能使与全等.
12. 如图,已知CE⊥CD,AD⊥AC,∠CBE=90°,DC=EC,若AC=8,AD=6,则AB的长为_____.
13. 如图,在中,,cm,cm,CD为AB边上的高,点E从点B出发,在直线BC上以2cm的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动_____s时,.
14. 现有一块如图所示的草地,经测量,,米,米,米,点是边的中点.小狗汪汪从点出发以米/秒的速度沿向点运动,同时小狗妞妞从点出发沿向点运动.当妞妞的速度为______米/秒时,能够在某一时刻使与全等.
三、解答题
15. 如图,点A,D,B,E在同一直线上,. 求证:.
16. 尺规作图:已知:,求作:,使得.(保留作图痕迹,不写作法)
17. 已知:如图,,,.求证:.
18. 如图,在四边形中,,连接,点E在上,连接,若,.
(1)求证:.
(2)若,求的度数.
19. (1)方法学习:数学兴趣小组活动时,张老师提出了如下问题:如图1,在中,,,求边上的中线的取值范围.
小明在组内经过合作交流,得到了如下的解决方法(如图2),
①延长到M,使得
②连接,通过三角形全等把、、转化在中;
③利用三角形的三边关系可得的取值范围为,从而得到的取值范围是 ;
方法总结:上述方法我们称为“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.
(2)请你写出图2中与的数量关系和位置关系,并加以证明.
(3)深入思考:如图3,是的中线,,,,请直接利用(2)的结论,试判断线段与的数量关系,并加以证明.
