第13章三角形的边角关系、命题与证明培优单元测试卷(含解析)
文档属性
| 名称 | 第13章三角形的边角关系、命题与证明培优单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 227.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-11 10:58:20 | ||
图片预览

文档简介
第13章三角形的边角关系、命题与证明培优单元测试卷
(考试时间:90分钟 满分:100分)
班级:_________ 姓名:___________________
一、填空题(本大题共10小题,每小题3分,满分30分)
1.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )2·1·c·n·j·y
A.1 B.2 C.3 D.4
2.已知三角形的一个外角为40°,则这个三角形一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
3.等腰三角形的两边长为2和5,则第三边的长为( )
A.2 B.3 C.5 D.8
4.如图所示,∠A, ∠1, ∠2的大小关系是( )
A. ∠A>∠1>∠2 B. ∠2>∠1>∠A
C. ∠A>∠2>∠1 D. ∠2>∠A>∠1
第4题图 第6题图 第8题图 第9题图
5.如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )
A.2 B.3 C.4 D.8www-2-1-cnjy-com
6.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A.30° B.40° C.60° D.70°2-1-c-n-j-y
7.下列命题中,逆命题是假命题的是( )
A.若两个角的和为90°,则它们互为余角
B.两锐角的和为90°的三角形是直角三角形
C.有一个外角是直角的三角形是直角三角形
D.等边三角形是等腰三角形
8.如图,AM是△ABC的中线,点D是AC边上的中点,△ABC的面积是8cm2,则△AMD的面积是( )【出处:21教育名师】
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
9.将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
A.45° B.50° C.60° D.75°
10.某超市失窃,大量的商品在夜间被罪犯用汽车运走,三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:①罪犯不在甲、乙、丙三人之外;②丙作案时总得有甲作从犯;③乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
二、填空题(本大题共6小题,每小题3分,满分18分)
11.把命题“同角的余角相等”改写成“如果…那么…”的形式 _________ .
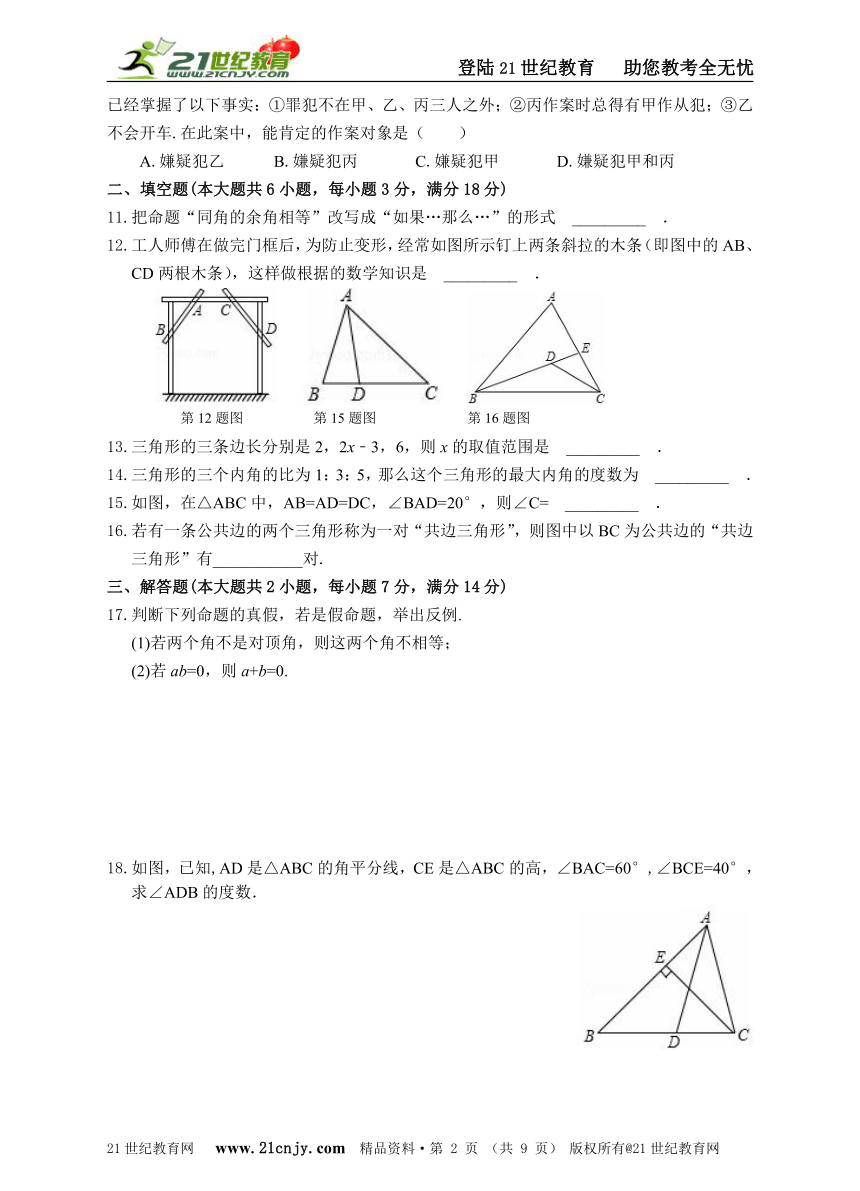
12.工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是 _________ .21·cn·jy·com
第12题图 第15题图 第16题图
13.三角形的三条边长分别是2,2x﹣3,6,则x的取值范围是 _________ .
14.三角形的三个内角的比为1:3:5,那么这个三角形的最大内角的度数为 _________ .
15.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C= _________ .
16.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有___________对.
三、解答题(本大题共2小题,每小题7分,满分14分)
17.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
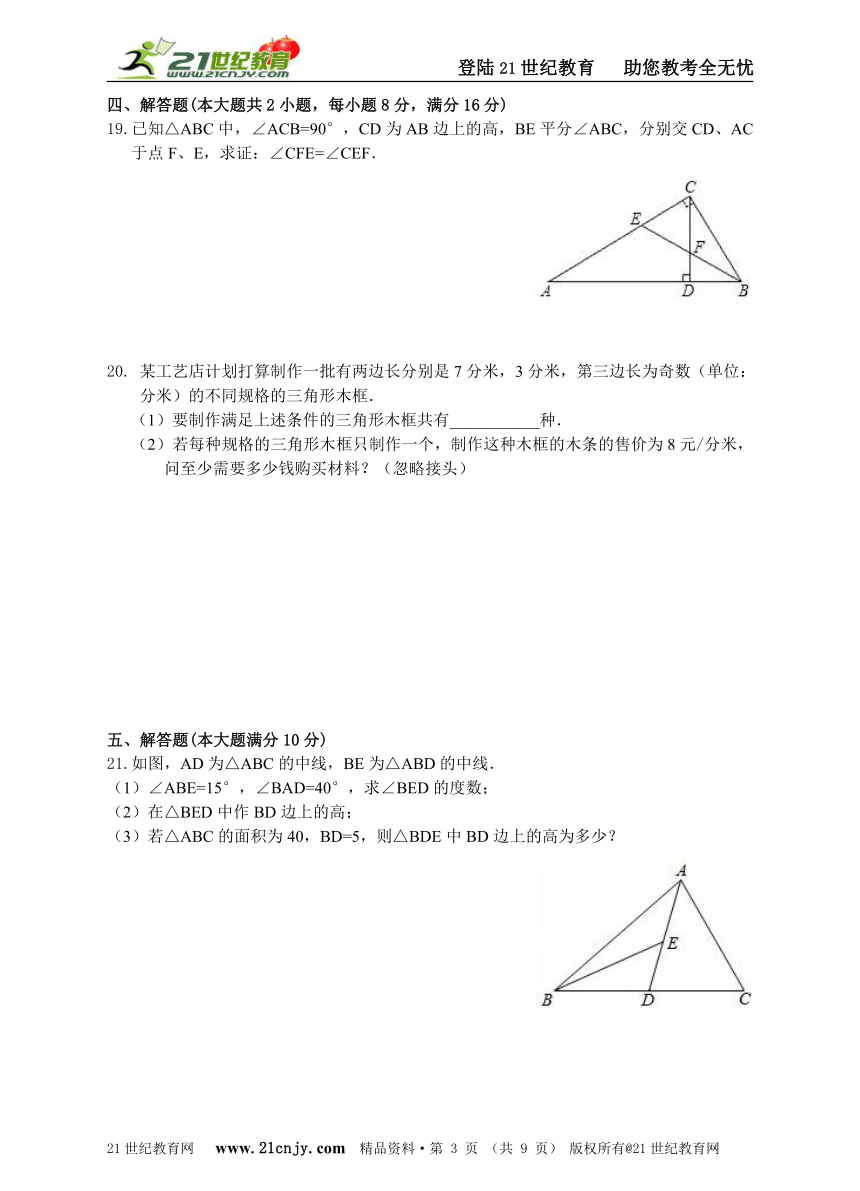
18.如图,已知,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
四、解答题(本大题共2小题,每小题8分,满分16分)
19.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.
20. 某工艺店计划打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.
(1)要制作满足上述条件的三角形木框共有___________种.
(2)若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元/分米,问至少需要多少钱购买材料?(忽略接头)
五、解答题(本大题满分10分)
21.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
六、解答题(本大题满分12分)
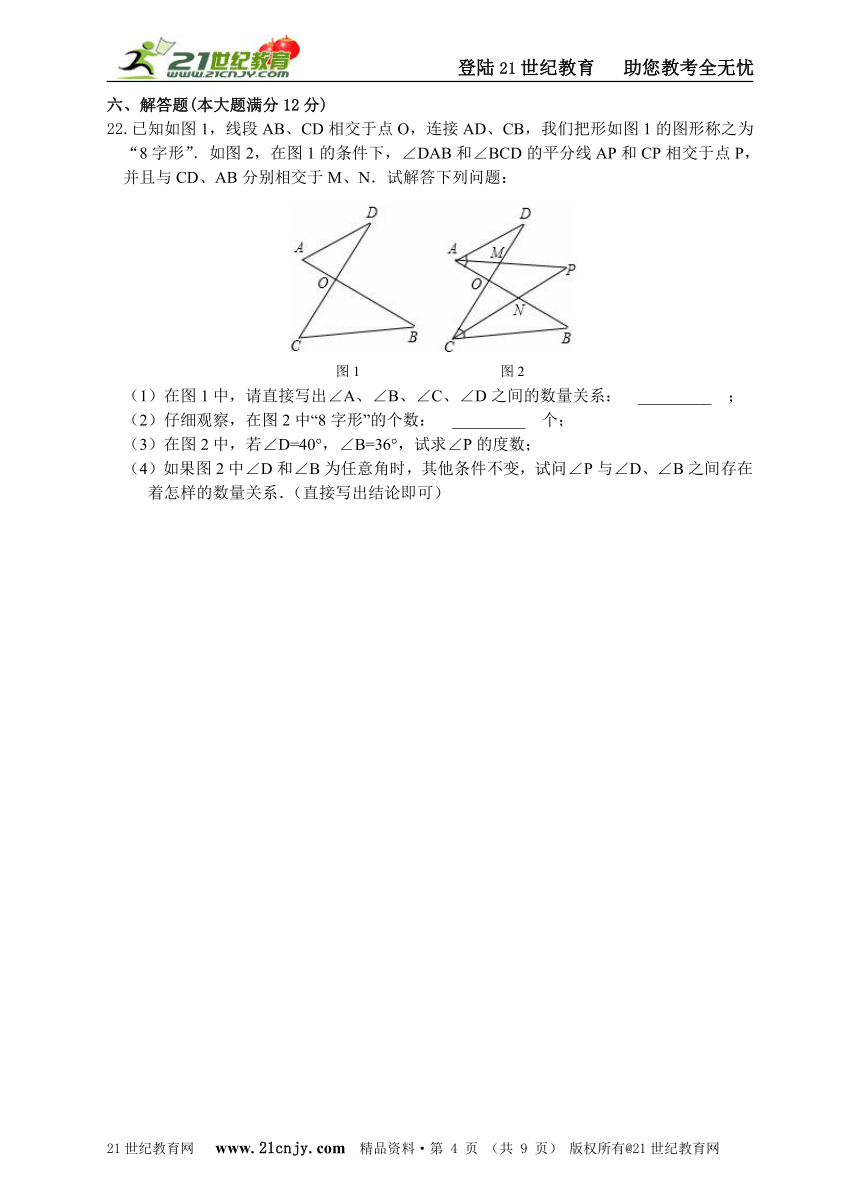
22.已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:www.21-cn-jy.com
图1 图2
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: _________ ;
(2)仔细观察,在图2中“8字形”的个数: _________ 个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)21·世纪*教育网
答案与解析
一、选择题
1. 考点:三角形三边关系.
解析:从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
解:四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
2. 考点:三角形按角分类.
解析:三角形的一个外角为40°,那么与它相邻的内角为140°,所以这个三角形为钝角三角形.
故选:B
4. 考点:三角形的外角.
解析:根据三角形的一个外角大于任意一个和它不相邻的一个内角,∠1是△ADC的外角,∠1>∠A,∠2是△EDC的外角,∠2>∠1,所以∠2>∠1>∠A,
故选:B
5.考点:三角形的三边关系.
解析:三角形的第三边小于另两边之和,大于另两边之差,所以第三边的取值范围是大于2 而小于8,在这个范围内的偶数有4,6.21世纪教育网版权所有
故选:C.
6. 考点:三角形的外角性质,平行线性质.
解析:先根据两直线平行,同位角相等,然后用“三角形的一个外角等于和它不相邻的两个内角的和”即可求得
故选:A
7.考点:命题
解析:将原命题的题设和结论交换位置后就得到它的逆命题,当然有时需要将文字重新调整,但不能改变命题的意思.【来源:21cnj*y.co*m】
A.“若两个角的和为90°,则它们互为余角”的逆命题是:如果两个角互为余角,那么这两个角的和为90°,这是个真命题,A正确;【版权所有:21教育】
B.“两锐角的和为90°的三角形是直角三角形”的逆命题是:直角三角形的两个锐角的和为90°,这是个真命题,B正确;21教育名师原创作品
C.“有一个外角是直角的三角形是直角三角形”的逆命题是:直角三角形中有一个外角是直角,这是个真命题,C正确;
D.“等边三角形是等腰三角形”的逆命题是:等腰三角形是等边三角形,这是个假命 题,D错误.
故选:D
8. 考点:三角形的中线、三角形的面积.
解析:根据三角形的中线将三角形分成面积相等的两个三角形(等底同高)求,
故选:A
10.考点:逻辑推理
解析:嫌疑犯可以肯定是这三个人,由于乙不会开车,所以有可能不是,丙作案时总得有甲作从犯,这样作案一定有两人,因此也不能肯定,最后最大嫌疑只有甲了,
故选C.
二、填空题
11.考点:命题与定理.
解析:命题有题设和结论两部分组成,通常写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论. 21*cnjy*com
解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
12.考点:三角形的稳定性.
解析:钉上两条斜拉的木条后,形成了两个三角形,故这种做法根据的是三角形的稳定性.
解:这样做根据的数学知识是:三角形的稳定性.
故答案为:三角形的稳定性.
13.考点:三角形三边关系;解一元一次不等式组
解析:根据三角形三边关系:①任意两边之和大于第三边;②任意两边之差小于第三边,即可得出第三边的取值范围.21*cnjy*com
解:∵三角形的两边长分别为2和6,
∴第三边长x的取值范围是:6﹣2<2x﹣3<6+2,
即:3.5<x<5.5.
故答案为:3.5<x<5.5.
14.考点:三角形内角和定理.
解析:设三角形三个角的度数分别为x,3x,5x,根据三角形内角和定理得x+3x+5x=180°,解得x=20°,然后计算5x即可.【来源:21·世纪·教育·网】
解:设三角形三个角的度数分别为x,3x,5x,
所以x+3x+5x=180°,解得x=20°,
所以5x=100°.
故答案为100°.
15.考点:三角形的外角性质;三角形内角和定理.
解析:先根据等腰三角形的性质及三角形内角和定理可求出∠B的度数,再根据三角形外角的性质可求出∠ADC的度数,再由三角形内角和定理解答即可.
解:∵AB=AD,∠BAD=20°,
∴∠B==80°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=80°+20°=100°,
∵AD=DC,
∴∠C== 40°.
16.考点:新定义,三角形.
解析:以BC为公共边的“共边三角形”有:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC三对.21cnjy.com
解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故选:B.
三、解答题
17.考点:反证法-举反例
解析:(1)假命题,如:两条直线平行,内错角相等;
(2)假命题,如:a=5,b=0,则ab=0,但a+b=5≠0.
四、解答题
19.考点:三角形的角平分线、中线和高
解析:题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.21教育网
证明:∵∠ACB=90°,
∴∠1+∠3=90°,
∵CD⊥AB,
∴∠2+∠4=90°,
又∵BE平分∠ABC,
∴∠1=∠2,
∴∠3=∠4,
∵∠4=∠5,
∴∠3=∠5,
即∠CFE=∠CEF.
20.考点:三角形三边关系.
解析:(1)根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,确定第三边的取值范围,从而确定符合条件的三角形的个数.(2)求出各三角形的周长的和,再乘以售价为8元╱分米,可求其所需钱数.
解:(1)三角形的第三边x满足:7﹣3<x<3+7,即4<x<10.因为第三边又为奇数,因而第三边可以为5、7或9.故要制作满足上述条件的三角形木框共有3种.
(2)制作这种木框的木条的长为:3+5+7+3+7+7+3+7+9=51(分米),
∴51×8=408(元).
答:至少需要408元购买材料.
五、解答题
六、解答题
(考试时间:90分钟 满分:100分)
班级:_________ 姓名:___________________
一、填空题(本大题共10小题,每小题3分,满分30分)
1.有3cm,6cm,8cm,9cm的四条线段,任选其中的三条线段组成一个三角形,则最多能组成三角形的个数为( )2·1·c·n·j·y
A.1 B.2 C.3 D.4
2.已知三角形的一个外角为40°,则这个三角形一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
3.等腰三角形的两边长为2和5,则第三边的长为( )
A.2 B.3 C.5 D.8
4.如图所示,∠A, ∠1, ∠2的大小关系是( )
A. ∠A>∠1>∠2 B. ∠2>∠1>∠A
C. ∠A>∠2>∠1 D. ∠2>∠A>∠1
第4题图 第6题图 第8题图 第9题图
5.如果三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是( )
A.2 B.3 C.4 D.8www-2-1-cnjy-com
6.如图,直线AB∥CD,∠A=70°,∠C=40°,则∠E等于( )
A.30° B.40° C.60° D.70°2-1-c-n-j-y
7.下列命题中,逆命题是假命题的是( )
A.若两个角的和为90°,则它们互为余角
B.两锐角的和为90°的三角形是直角三角形
C.有一个外角是直角的三角形是直角三角形
D.等边三角形是等腰三角形
8.如图,AM是△ABC的中线,点D是AC边上的中点,△ABC的面积是8cm2,则△AMD的面积是( )【出处:21教育名师】
A.2 cm2 B.4 cm2 C.6 cm2 D.8 cm2
9.将一副直角三角尺如图放置,已知AE∥BC,则∠AFD的度数是( )
A.45° B.50° C.60° D.75°
10.某超市失窃,大量的商品在夜间被罪犯用汽车运走,三个嫌疑犯被警察局传讯,警察局已经掌握了以下事实:①罪犯不在甲、乙、丙三人之外;②丙作案时总得有甲作从犯;③乙不会开车.在此案中,能肯定的作案对象是( )
A.嫌疑犯乙 B.嫌疑犯丙 C.嫌疑犯甲 D.嫌疑犯甲和丙
二、填空题(本大题共6小题,每小题3分,满分18分)
11.把命题“同角的余角相等”改写成“如果…那么…”的形式 _________ .
12.工人师傅在做完门框后,为防止变形,经常如图所示钉上两条斜拉的木条(即图中的AB、CD两根木条),这样做根据的数学知识是 _________ .21·cn·jy·com
第12题图 第15题图 第16题图
13.三角形的三条边长分别是2,2x﹣3,6,则x的取值范围是 _________ .
14.三角形的三个内角的比为1:3:5,那么这个三角形的最大内角的度数为 _________ .
15.如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C= _________ .
16.若有一条公共边的两个三角形称为一对“共边三角形”,则图中以BC为公共边的“共边三角形”有___________对.
三、解答题(本大题共2小题,每小题7分,满分14分)
17.判断下列命题的真假,若是假命题,举出反例.
(1)若两个角不是对顶角,则这两个角不相等;
(2)若ab=0,则a+b=0.
18.如图,已知,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
四、解答题(本大题共2小题,每小题8分,满分16分)
19.已知△ABC中,∠ACB=90°,CD为AB边上的高,BE平分∠ABC,分别交CD、AC于点F、E,求证:∠CFE=∠CEF.
20. 某工艺店计划打算制作一批有两边长分别是7分米,3分米,第三边长为奇数(单位:分米)的不同规格的三角形木框.
(1)要制作满足上述条件的三角形木框共有___________种.
(2)若每种规格的三角形木框只制作一个,制作这种木框的木条的售价为8元/分米,问至少需要多少钱购买材料?(忽略接头)
五、解答题(本大题满分10分)
21.如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
六、解答题(本大题满分12分)
22.已知如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:www.21-cn-jy.com
图1 图2
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: _________ ;
(2)仔细观察,在图2中“8字形”的个数: _________ 个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)21·世纪*教育网
答案与解析
一、选择题
1. 考点:三角形三边关系.
解析:从4条线段里任取3条线段组合,可有4种情况,看哪种情况不符合三角形三边关系,舍去即可.
解:四条木棒的所有组合:3,6,8和3,6,9和6,8,9和3,8,9;
只有3,6,8和6,8,9;3,8,9能组成三角形.
故选:C.
2. 考点:三角形按角分类.
解析:三角形的一个外角为40°,那么与它相邻的内角为140°,所以这个三角形为钝角三角形.
故选:B
4. 考点:三角形的外角.
解析:根据三角形的一个外角大于任意一个和它不相邻的一个内角,∠1是△ADC的外角,∠1>∠A,∠2是△EDC的外角,∠2>∠1,所以∠2>∠1>∠A,
故选:B
5.考点:三角形的三边关系.
解析:三角形的第三边小于另两边之和,大于另两边之差,所以第三边的取值范围是大于2 而小于8,在这个范围内的偶数有4,6.21世纪教育网版权所有
故选:C.
6. 考点:三角形的外角性质,平行线性质.
解析:先根据两直线平行,同位角相等,然后用“三角形的一个外角等于和它不相邻的两个内角的和”即可求得
故选:A
7.考点:命题
解析:将原命题的题设和结论交换位置后就得到它的逆命题,当然有时需要将文字重新调整,但不能改变命题的意思.【来源:21cnj*y.co*m】
A.“若两个角的和为90°,则它们互为余角”的逆命题是:如果两个角互为余角,那么这两个角的和为90°,这是个真命题,A正确;【版权所有:21教育】
B.“两锐角的和为90°的三角形是直角三角形”的逆命题是:直角三角形的两个锐角的和为90°,这是个真命题,B正确;21教育名师原创作品
C.“有一个外角是直角的三角形是直角三角形”的逆命题是:直角三角形中有一个外角是直角,这是个真命题,C正确;
D.“等边三角形是等腰三角形”的逆命题是:等腰三角形是等边三角形,这是个假命 题,D错误.
故选:D
8. 考点:三角形的中线、三角形的面积.
解析:根据三角形的中线将三角形分成面积相等的两个三角形(等底同高)求,
故选:A
10.考点:逻辑推理
解析:嫌疑犯可以肯定是这三个人,由于乙不会开车,所以有可能不是,丙作案时总得有甲作从犯,这样作案一定有两人,因此也不能肯定,最后最大嫌疑只有甲了,
故选C.
二、填空题
11.考点:命题与定理.
解析:命题有题设和结论两部分组成,通常写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论. 21*cnjy*com
解:根据命题的特点,可以改写为:“如果两个角是同一个角的余角,那么这两个角相等”,
故答案为:如果两个角是同一个角的余角,那么这两个角相等.
12.考点:三角形的稳定性.
解析:钉上两条斜拉的木条后,形成了两个三角形,故这种做法根据的是三角形的稳定性.
解:这样做根据的数学知识是:三角形的稳定性.
故答案为:三角形的稳定性.
13.考点:三角形三边关系;解一元一次不等式组
解析:根据三角形三边关系:①任意两边之和大于第三边;②任意两边之差小于第三边,即可得出第三边的取值范围.21*cnjy*com
解:∵三角形的两边长分别为2和6,
∴第三边长x的取值范围是:6﹣2<2x﹣3<6+2,
即:3.5<x<5.5.
故答案为:3.5<x<5.5.
14.考点:三角形内角和定理.
解析:设三角形三个角的度数分别为x,3x,5x,根据三角形内角和定理得x+3x+5x=180°,解得x=20°,然后计算5x即可.【来源:21·世纪·教育·网】
解:设三角形三个角的度数分别为x,3x,5x,
所以x+3x+5x=180°,解得x=20°,
所以5x=100°.
故答案为100°.
15.考点:三角形的外角性质;三角形内角和定理.
解析:先根据等腰三角形的性质及三角形内角和定理可求出∠B的度数,再根据三角形外角的性质可求出∠ADC的度数,再由三角形内角和定理解答即可.
解:∵AB=AD,∠BAD=20°,
∴∠B==80°,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=80°+20°=100°,
∵AD=DC,
∴∠C== 40°.
16.考点:新定义,三角形.
解析:以BC为公共边的“共边三角形”有:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC三对.21cnjy.com
解:△BDC与△BEC、△BDC与△BAC、△BEC与△BAC共三对.
故选:B.
三、解答题
17.考点:反证法-举反例
解析:(1)假命题,如:两条直线平行,内错角相等;
(2)假命题,如:a=5,b=0,则ab=0,但a+b=5≠0.
四、解答题
19.考点:三角形的角平分线、中线和高
解析:题目中有两对直角,可得两对角互余,由角平分线及对顶角可得两对角相等,然后利用等量代换可得答案.21教育网
证明:∵∠ACB=90°,
∴∠1+∠3=90°,
∵CD⊥AB,
∴∠2+∠4=90°,
又∵BE平分∠ABC,
∴∠1=∠2,
∴∠3=∠4,
∵∠4=∠5,
∴∠3=∠5,
即∠CFE=∠CEF.
20.考点:三角形三边关系.
解析:(1)根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,确定第三边的取值范围,从而确定符合条件的三角形的个数.(2)求出各三角形的周长的和,再乘以售价为8元╱分米,可求其所需钱数.
解:(1)三角形的第三边x满足:7﹣3<x<3+7,即4<x<10.因为第三边又为奇数,因而第三边可以为5、7或9.故要制作满足上述条件的三角形木框共有3种.
(2)制作这种木框的木条的长为:3+5+7+3+7+7+3+7+9=51(分米),
∴51×8=408(元).
答:至少需要408元购买材料.
五、解答题
六、解答题
