江西省吉安市万安县中2023-2024学年高二上学期开学考试数学试题(含解析)
文档属性
| 名称 | 江西省吉安市万安县中2023-2024学年高二上学期开学考试数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 07:46:25 | ||
图片预览




文档简介
万安县中2023-2024学年高二上学期开学考试
数学
一、单选题(每题5分,共40分)
1.等于( )
A. B. C. D.
2.下列说法中正确的是( )
A.锐角是第一象限角 B.终边相等的角必相等
C.小于的角一定在第一象限 D.第二象限角必大于第一象限角
3.已知,,则( )
A. B. C. D.
4.( )
A. B. C. D.
5.设i为虚数单位,若复数,则复数的实部与虚部的和为( )
A. B.1 C.0 D.2
6.“今有城,下广四丈,上广二丈,高五丈,袤两百丈.”这是我国古代数学名著《九章算术》卷第五“商功”中的问题.意思为“现有城(如图,等腰梯形的直棱柱体),下底长4丈,上底长2丈,高5丈,纵长200丈(1丈=10尺)”,则该问题中“城”的体积等于( )
A.立方尺 B.立方尺 C.立方尺 D.立方尺
7.如图,在正三棱柱中,若,,点D是棱的中点,点E在棱上,则三棱锥的体积为( )
A.1 B.2 C. D.
8.在斜三角形中,角的对边分别为,点满足,且,则的面积为( )
A. B. C. D.
二、多选题(每题5分,共20分)
9.已知下列各角:①;②;③;④,其中是第二象限角的是( )
A.① B.② C.③ D.④
10.已知函数,则说法正确的是( )
A.的图象关于点对称 B.的图象关于直线对称
C.为奇函数 D.为偶函数
11.在正方体中,E,F,G分别为BC,,的中点,则( )
A.直线与直线AF异面
B.直线与平面AEF平行
C.平面AEF截正方体所得的截面是等腰梯形
D.三棱锥A-CEF的体积是正方体体积的
12.如图,在菱形中,,延长边至点,使得.动点从点出发,沿菱形的边按逆时针方向运动一周回到点,若,则( )
A.满足的点有且只有一个
B.满足的点有两个
C.存在最小值
D.不存在最大值
三、填空题(共20分)
13.已知向量满足,则 .
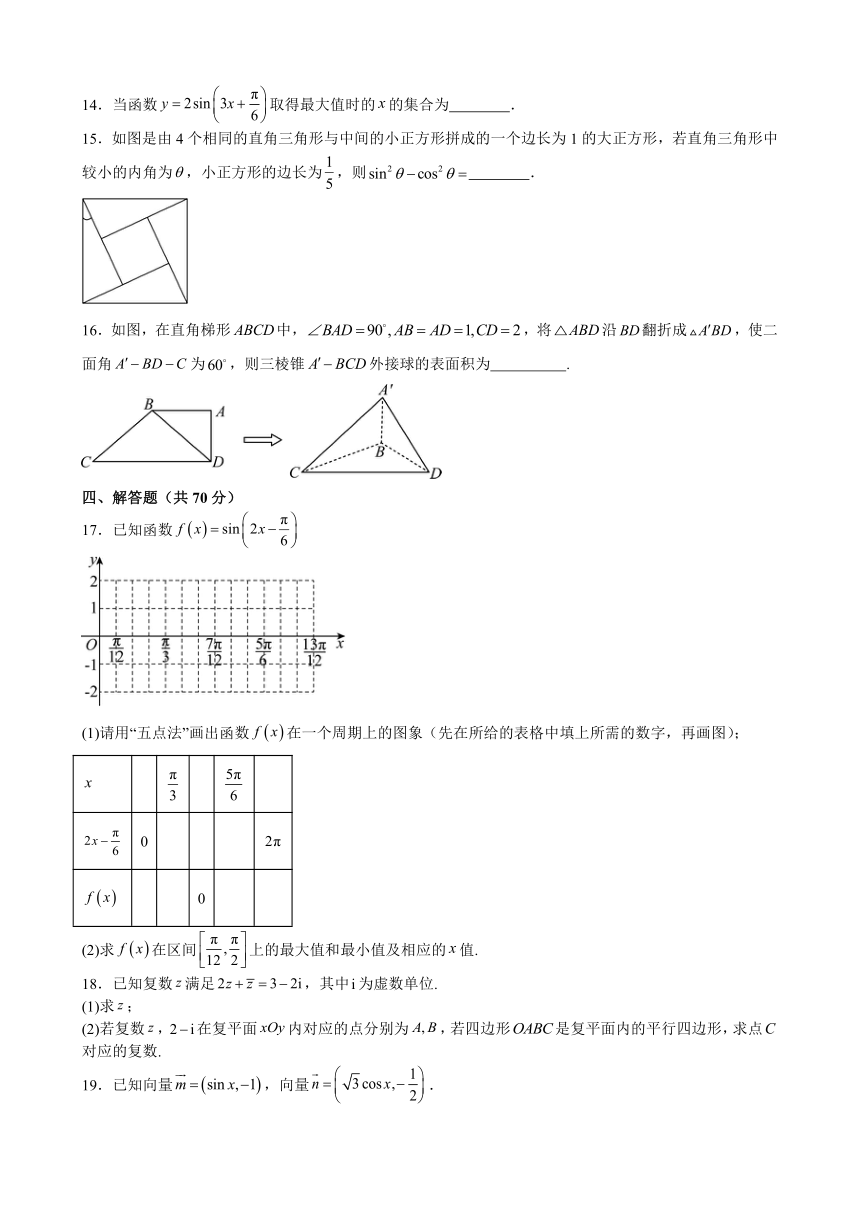
14.当函数取得最大值时的的集合为 .
15.如图是由4个相同的直角三角形与中间的小正方形拼成的一个边长为1的大正方形,若直角三角形中较小的内角为,小正方形的边长为,则 .
16.如图,在直角梯形中,,将沿翻折成,使二面角为,则三棱锥外接球的表面积为 .
四、解答题(共70分)
17.已知函数
(1)请用“五点法”画出函数在一个周期上的图象(先在所给的表格中填上所需的数字,再画图);
0
0
(2)求在区间上的最大值和最小值及相应的值.
18.已知复数满足,其中为虚数单位.
(1)求;
(2)若复数,在复平面内对应的点分别为,若四边形是复平面内的平行四边形,求点对应的复数.
19.已知向量,向量.
(1)当时,求的值;
(2)设函数,且,求的最大值以及对应的x的值.
20.①,②,③三个条件中任选一个,补充在下面的问题中,并进行解答.
已知△ABC的三边a,b,c所对的角分别为A,B,C,若,______,
(1)求B;
(2)求的面积.
21.重庆是我国著名的“火炉”城市之一,如图,重庆某避暑山庄O为吸引游客,准备在门前两条小路OA和OB之间修建一处弓形花园,使之有着类似“冰淇淋”般的凉爽感,已知,弓形花园的弦长,记弓形花园的顶点为,设.
(1)将用含有的关系式表示出来;
(2)该山庄准备在点处修建喷泉,为获取更好的观景视野,如何设计的长度,才使得喷泉与山庄的距离的值最大?
22.如图,已知矩形,,M是AD的中点,现将沿着BM翻折至.
(1)若,求证:平面平面;
(2)求二面角的正弦值的最大值.
1.D
因为,
故选:D.
2.A
锐角是指大于小于的角,故其在第一象限,即A正确;
选项B.终边相等的角必相等,两角可以相差整数倍,故错误;
选项C.小于的角不一定在第一象限,也可以为负角,故错误;
选项D.根据任意角的定义,第二象限角可以为负角,第一象限角可以为正角,此时第二象限角小于第一象限角,故错误.
故选:A
3.A
因为,,
所以,
故选:A
4.A
.
故选:A
5.D
,
则其实部为,虚部为,故实部与虚部之和为2,
故选:D.
6.D
依题意,该柱体的体积为立方尺.
故选:D
7.C
在正三棱柱中,若,,
点是棱的中点,点在棱上,
,
点到平面的距离,
三棱锥的体积为:
.
故选:C.
8.A
因为,
由余弦定理得,
又因为是斜三角形,所以,所以,
由正弦定理得,因为,
所以,所以,
所以,所以,
所以,
因为,
化简得,解得或(舍去),
所以,
设边的中点为,则,
因为,所以,
即为的中点,所以:.
故选:A.
9.CD
对于①,,而是第三象限角,①不是;
对于②,角的终边为x轴非正半轴,②不是;
对于③,,是第二象限角,③是;
对于④,,是第二象限角,④是.
故选:CD
10.AC
对于A选项,因为,
所以,
的图象关于点对称,所以A选项正确.
对于B选项,由,
知的图象不关于直线对称,所以B选项错误.
对于C选项,由,
知为奇函数,所以C选项正确.
对于D选项,因为,
,
,所以不为偶函数,所以D选项错误.
故选:AC.
11.ABC
对于选项A,易知AF与异面,选项A正确;
对于选项B,取的中点为M,连接、GM,则,,易证,从而,选项B正确;
对于选项C,连接,,易知平面AEF截正方体所得的截面为等腰梯形,选项C正确;
对于选项D.设正方体棱长为a,三棱锥A-CEF的体积,选项D错误.
故选:ABC.
12.BC
建立如图所示的平面直角坐标系,设菱形的边长为1,,则
,
所以,,
由,得,
所以,所以,
①当点在上时,,且,
所以;
②当点在(不含点B)上时,则,所以,化简,
所以,
因为,所以,即;
③当点在(不含点C)上时,,且,
所以,即,所以;
④当点在(不含点A、D)上时,则,所以,化简,
所以,
因为,所以,所以;
对于A,由①知,当时,,此时点与点重合;
由④可知当时,,,此时点在的中点处;
其它均不可能,所以这样的点有两个,所以A错误,
对于B,由②知,当时,,,此时点在的中点;
由③知,当时,,,此时点在点处;
其它均不可能,所以这样的点有两个,所以B正确,
对于CD,由①②③④可得:
当,即点为点时,取到最小值0;
当,即点为点时,取到最大值3,所以C正确,D错误,
故选:BC.
13./
由题意,
,所以,
故答案为:
14.
依题意令,,
解得,,
所以函数取得最大值时的的集合为.
故答案为:
15.
如图所示,在直角三角形中,,,,
则,,所以,,
所以,解得,,
所以.
故答案为:
16.
解:如图,设外接球的球心为,半径为为中点,为中点,
因为,所以,∥,
又因为,,
所以,
所以,,
所以,,
所以为二面角的平面角,
所以,
作于,
因为,,,
所以平面,
又因为平面,
所以 ,
又因为,,
则平面,所以∥,
则有,
即,
由题意可求得:,
设,
由题上式可得:,
求得:,从而求得:,
故三棱锥外接球的表面积为.
故答案为:
17.(1)答案见解析;
(2)时,取最小值0;时,取最大值1.
(1)分别令,可得:
x
0
0 1 0 0
画出函数在一个周期的图像如图所示:
(2)因为,所以,
所以当,即时,取最小值0;
当,即时,取最大值1.
18.(1)
(2)
(1)设,则,
故,
所以解得:,
∴;
(2)由(1)得:,
因为四边形是复平面内的平行四边形
所以
故点对应的复数为.
19.(1)
(2),
(1)因为,所以,解得.
(2)
,
又因为,所以,
所以当,即时取得最大值为3.
20.(1)条件选择见解析,;
(2)或.
(1)若选①,,
可得,可得:,
因为,可得,可得,可得;
若选②,,由正弦定理可得,
因为,则,可得,即,
因为,可得;
若选③,因为,可得,
可得,因为,可得;
(2)结合(1)因为,利用正弦定理可得,所以,
因为,所以或,
当时,,
因为,所以,,
可得:,
当时,则,
又因为,所以,.
所以的面积为或.
21.(1),
(2)答案见解析
(1)因为,,
所以,.
(2)因为,
所以,
在中,由余弦定理易得,
因为,所以,
当,即时,
取最大值取最大值,
此时,
,
故当时,取最大值.
22.(1)证明见解析
(2)
(1)由题意矩形中,,M是AD的中点,
可知, ,
设O为中点,连接,则,
又,,
故,
又 ,O为中点,故,而,
故,故,
而平面,故平面,
平面,故平面平面;
(2)由(1)可知,将沿着BM翻折至平面平面时,
二面角逐渐增大,
当平面平面时,作,垂足为E,连接,
因为O为中点,则E为中点,此时;
由于平面,平面,故,
平面,故平面,
则为二面角的平面角,而,
故;
下面考虑翻折到越过平面平面时的位置后的情况:
设Q为中点,连接,则四边形为正方形,
连接,则O在上,则,
平面,故平面,
平面,故平面平面,
平面平面,作,垂足为F,
则平面,平面,故,,
作,垂足为G,连接,
平面,故平面,
故为二面角的平面角,
设,当时,二面角的正弦值为0;
当时,,
作,垂足为H,则四边形为矩形,
则,故,
故
,
由于,故,故,
当且仅当,即时等号成立,
即二面角的正切值的最大值为,
此时二面角的正弦值的最大值,
由于,故二面角的正弦值的最大值.
数学
一、单选题(每题5分,共40分)
1.等于( )
A. B. C. D.
2.下列说法中正确的是( )
A.锐角是第一象限角 B.终边相等的角必相等
C.小于的角一定在第一象限 D.第二象限角必大于第一象限角
3.已知,,则( )
A. B. C. D.
4.( )
A. B. C. D.
5.设i为虚数单位,若复数,则复数的实部与虚部的和为( )
A. B.1 C.0 D.2
6.“今有城,下广四丈,上广二丈,高五丈,袤两百丈.”这是我国古代数学名著《九章算术》卷第五“商功”中的问题.意思为“现有城(如图,等腰梯形的直棱柱体),下底长4丈,上底长2丈,高5丈,纵长200丈(1丈=10尺)”,则该问题中“城”的体积等于( )
A.立方尺 B.立方尺 C.立方尺 D.立方尺
7.如图,在正三棱柱中,若,,点D是棱的中点,点E在棱上,则三棱锥的体积为( )
A.1 B.2 C. D.
8.在斜三角形中,角的对边分别为,点满足,且,则的面积为( )
A. B. C. D.
二、多选题(每题5分,共20分)
9.已知下列各角:①;②;③;④,其中是第二象限角的是( )
A.① B.② C.③ D.④
10.已知函数,则说法正确的是( )
A.的图象关于点对称 B.的图象关于直线对称
C.为奇函数 D.为偶函数
11.在正方体中,E,F,G分别为BC,,的中点,则( )
A.直线与直线AF异面
B.直线与平面AEF平行
C.平面AEF截正方体所得的截面是等腰梯形
D.三棱锥A-CEF的体积是正方体体积的
12.如图,在菱形中,,延长边至点,使得.动点从点出发,沿菱形的边按逆时针方向运动一周回到点,若,则( )
A.满足的点有且只有一个
B.满足的点有两个
C.存在最小值
D.不存在最大值
三、填空题(共20分)
13.已知向量满足,则 .
14.当函数取得最大值时的的集合为 .
15.如图是由4个相同的直角三角形与中间的小正方形拼成的一个边长为1的大正方形,若直角三角形中较小的内角为,小正方形的边长为,则 .
16.如图,在直角梯形中,,将沿翻折成,使二面角为,则三棱锥外接球的表面积为 .
四、解答题(共70分)
17.已知函数
(1)请用“五点法”画出函数在一个周期上的图象(先在所给的表格中填上所需的数字,再画图);
0
0
(2)求在区间上的最大值和最小值及相应的值.
18.已知复数满足,其中为虚数单位.
(1)求;
(2)若复数,在复平面内对应的点分别为,若四边形是复平面内的平行四边形,求点对应的复数.
19.已知向量,向量.
(1)当时,求的值;
(2)设函数,且,求的最大值以及对应的x的值.
20.①,②,③三个条件中任选一个,补充在下面的问题中,并进行解答.
已知△ABC的三边a,b,c所对的角分别为A,B,C,若,______,
(1)求B;
(2)求的面积.
21.重庆是我国著名的“火炉”城市之一,如图,重庆某避暑山庄O为吸引游客,准备在门前两条小路OA和OB之间修建一处弓形花园,使之有着类似“冰淇淋”般的凉爽感,已知,弓形花园的弦长,记弓形花园的顶点为,设.
(1)将用含有的关系式表示出来;
(2)该山庄准备在点处修建喷泉,为获取更好的观景视野,如何设计的长度,才使得喷泉与山庄的距离的值最大?
22.如图,已知矩形,,M是AD的中点,现将沿着BM翻折至.
(1)若,求证:平面平面;
(2)求二面角的正弦值的最大值.
1.D
因为,
故选:D.
2.A
锐角是指大于小于的角,故其在第一象限,即A正确;
选项B.终边相等的角必相等,两角可以相差整数倍,故错误;
选项C.小于的角不一定在第一象限,也可以为负角,故错误;
选项D.根据任意角的定义,第二象限角可以为负角,第一象限角可以为正角,此时第二象限角小于第一象限角,故错误.
故选:A
3.A
因为,,
所以,
故选:A
4.A
.
故选:A
5.D
,
则其实部为,虚部为,故实部与虚部之和为2,
故选:D.
6.D
依题意,该柱体的体积为立方尺.
故选:D
7.C
在正三棱柱中,若,,
点是棱的中点,点在棱上,
,
点到平面的距离,
三棱锥的体积为:
.
故选:C.
8.A
因为,
由余弦定理得,
又因为是斜三角形,所以,所以,
由正弦定理得,因为,
所以,所以,
所以,所以,
所以,
因为,
化简得,解得或(舍去),
所以,
设边的中点为,则,
因为,所以,
即为的中点,所以:.
故选:A.
9.CD
对于①,,而是第三象限角,①不是;
对于②,角的终边为x轴非正半轴,②不是;
对于③,,是第二象限角,③是;
对于④,,是第二象限角,④是.
故选:CD
10.AC
对于A选项,因为,
所以,
的图象关于点对称,所以A选项正确.
对于B选项,由,
知的图象不关于直线对称,所以B选项错误.
对于C选项,由,
知为奇函数,所以C选项正确.
对于D选项,因为,
,
,所以不为偶函数,所以D选项错误.
故选:AC.
11.ABC
对于选项A,易知AF与异面,选项A正确;
对于选项B,取的中点为M,连接、GM,则,,易证,从而,选项B正确;
对于选项C,连接,,易知平面AEF截正方体所得的截面为等腰梯形,选项C正确;
对于选项D.设正方体棱长为a,三棱锥A-CEF的体积,选项D错误.
故选:ABC.
12.BC
建立如图所示的平面直角坐标系,设菱形的边长为1,,则
,
所以,,
由,得,
所以,所以,
①当点在上时,,且,
所以;
②当点在(不含点B)上时,则,所以,化简,
所以,
因为,所以,即;
③当点在(不含点C)上时,,且,
所以,即,所以;
④当点在(不含点A、D)上时,则,所以,化简,
所以,
因为,所以,所以;
对于A,由①知,当时,,此时点与点重合;
由④可知当时,,,此时点在的中点处;
其它均不可能,所以这样的点有两个,所以A错误,
对于B,由②知,当时,,,此时点在的中点;
由③知,当时,,,此时点在点处;
其它均不可能,所以这样的点有两个,所以B正确,
对于CD,由①②③④可得:
当,即点为点时,取到最小值0;
当,即点为点时,取到最大值3,所以C正确,D错误,
故选:BC.
13./
由题意,
,所以,
故答案为:
14.
依题意令,,
解得,,
所以函数取得最大值时的的集合为.
故答案为:
15.
如图所示,在直角三角形中,,,,
则,,所以,,
所以,解得,,
所以.
故答案为:
16.
解:如图,设外接球的球心为,半径为为中点,为中点,
因为,所以,∥,
又因为,,
所以,
所以,,
所以,,
所以为二面角的平面角,
所以,
作于,
因为,,,
所以平面,
又因为平面,
所以 ,
又因为,,
则平面,所以∥,
则有,
即,
由题意可求得:,
设,
由题上式可得:,
求得:,从而求得:,
故三棱锥外接球的表面积为.
故答案为:
17.(1)答案见解析;
(2)时,取最小值0;时,取最大值1.
(1)分别令,可得:
x
0
0 1 0 0
画出函数在一个周期的图像如图所示:
(2)因为,所以,
所以当,即时,取最小值0;
当,即时,取最大值1.
18.(1)
(2)
(1)设,则,
故,
所以解得:,
∴;
(2)由(1)得:,
因为四边形是复平面内的平行四边形
所以
故点对应的复数为.
19.(1)
(2),
(1)因为,所以,解得.
(2)
,
又因为,所以,
所以当,即时取得最大值为3.
20.(1)条件选择见解析,;
(2)或.
(1)若选①,,
可得,可得:,
因为,可得,可得,可得;
若选②,,由正弦定理可得,
因为,则,可得,即,
因为,可得;
若选③,因为,可得,
可得,因为,可得;
(2)结合(1)因为,利用正弦定理可得,所以,
因为,所以或,
当时,,
因为,所以,,
可得:,
当时,则,
又因为,所以,.
所以的面积为或.
21.(1),
(2)答案见解析
(1)因为,,
所以,.
(2)因为,
所以,
在中,由余弦定理易得,
因为,所以,
当,即时,
取最大值取最大值,
此时,
,
故当时,取最大值.
22.(1)证明见解析
(2)
(1)由题意矩形中,,M是AD的中点,
可知, ,
设O为中点,连接,则,
又,,
故,
又 ,O为中点,故,而,
故,故,
而平面,故平面,
平面,故平面平面;
(2)由(1)可知,将沿着BM翻折至平面平面时,
二面角逐渐增大,
当平面平面时,作,垂足为E,连接,
因为O为中点,则E为中点,此时;
由于平面,平面,故,
平面,故平面,
则为二面角的平面角,而,
故;
下面考虑翻折到越过平面平面时的位置后的情况:
设Q为中点,连接,则四边形为正方形,
连接,则O在上,则,
平面,故平面,
平面,故平面平面,
平面平面,作,垂足为F,
则平面,平面,故,,
作,垂足为G,连接,
平面,故平面,
故为二面角的平面角,
设,当时,二面角的正弦值为0;
当时,,
作,垂足为H,则四边形为矩形,
则,故,
故
,
由于,故,故,
当且仅当,即时等号成立,
即二面角的正切值的最大值为,
此时二面角的正弦值的最大值,
由于,故二面角的正弦值的最大值.
同课章节目录
