华师版数学八年级上册 13.4.1 尺规作图 课件(共18张PPT)
文档属性
| 名称 | 华师版数学八年级上册 13.4.1 尺规作图 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 600.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 09:14:19 | ||
图片预览






文档简介
(共18张PPT)
13.4 尺规作图
第1课时 尺规作图(1)
学习目标
掌握尺规作图的定义,知道什么是尺规作图.
能用尺规作图完成以下基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知角的平分线;
温故知新
在数学中,我们在作图时会用到哪些工具?
刻度尺、三角尺、量角器、圆规等.
如果只有圆规和没有刻度的直尺,还能作出符合条件的几何图形吗?
尺规作图的定义:
新知
我们把只能使用圆规和没有刻度的直尺这两种工具作几何图形的方法称为尺规作图.
想一想,学过的几何图形中,哪些可以用尺规作图得到?
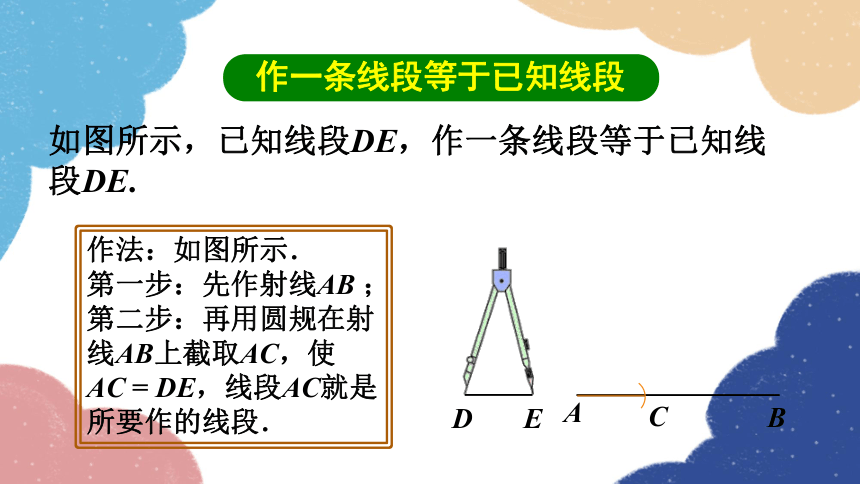
作一条线段等于已知线段
如图所示,已知线段DE,作一条线段等于已知线段DE.
作法:如图所示.
第一步:先作射线AB ;
第二步:再用圆规在射线AB上截取AC,使
AC = DE,线段AC就是所要作的线段.
D
E
A
B
C
【例1】如图,已知线段a,b(a>b),求作一条线段AB,使AB = 2(a-b).
例题
a
b
分析: AB = 2(a-b) = 2a-2b,故只需先作2a,再作2b,将2a中和2b重合部分去掉即可.
【例1】如图,已知线段a,b(a>b),求作一条线段AB,使AB = 2(a-b).
a
b
解:如图,
(1)作射线OP;
(2)在射线OP上顺次截取OM = MB = a;
(3)在线段OB上顺次截取ON = NA = b,则线段
AB就是所求作的线段.
A
B
O
P
M
N
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
第一步:作射线O′A′;
第二步:以点O为圆心,以适当长为半径作弧,交OA于点C,交OB于点D;
第三步:以点O′为圆心,以OC长为半径作弧,交O′A′于点C′;
A′
O′
C
D
C′
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
第四步:以点C′为圆心,以CD长为半径作弧,交前一条弧于
点D′;
第五步:经过点D′作射线O′B′,∠A′O′B′就是所求作的角,如图.
A′
C
D
C′
O′
D′
B′
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
A′
C′
O′
C
D
D′
B′
第四步:以点C′为圆心,以CD长为半径作弧,交前一条弧于
点D′;
第五步:经过点D′作射线O′B′,∠A′O′B′就是所求作的角,如图.
思考:为什么作出的角和已知角相等?理论依据是什么?
你知道如何用尺规作图作一个角等于刚刚所作角的二倍吗?
如何作已知角的平分线呢?
作已知角的平分线
如图,∠AOB 为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.
第一步:在射线OA、AB上,分别截取OD、OE.使OD = OE;
第二步:分别以点D和点E为圆心、
适当长(大于线段DE长的一半)为
半径作圆弧,在∠AOB内,两弧
交于点C;
A
O
C
E
D
B
作已知角的平分线
如图,∠AOB 为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.
第三步:作射线OC.
射线OC就是所要求作的∠AOB的平分线.
A
O
E
D
B
如何证明OC是∠AOB的平分线?
C
如图,连结EC、DC .
∵OD = OE,DC = EC,OC = OC,
∴△OCD≌△OCE(S.S.S.),
∴∠AOC =∠BOC (全等三角形的对应
角相等).
为简化推理格式,今后只注明主要依据,省略“已知”、“等量代换” 等依据.
1.如图,用尺规作图:“过点C作CN∥OA”,其作图依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角相等,两直线平行
D.同旁内角互补,两直线平行
练习
B
S.S.S.
3.如图,已知∠AOB和线段PQ,利用“同位角相等,两直线平行”用尺规作图:“过点C作CN∥OA”,并作∠BCN的平分线,截取
CM = PQ.(保留作图痕迹)
练习
A
O
C
B
N
M
Q
P
.
本节课学习了哪些内容?
1.什么是尺规作图:
我们把只能使用圆规和没有刻度的直尺这两种工具作几何图形的方法称为尺规作图.
2. 尺规的基本作图:
①作一条线段等于已知线段;
②作一个角等于已知角;
③作已知角的平分线.
课堂小结
13.4 尺规作图
第1课时 尺规作图(1)
学习目标
掌握尺规作图的定义,知道什么是尺规作图.
能用尺规作图完成以下基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知角的平分线;
温故知新
在数学中,我们在作图时会用到哪些工具?
刻度尺、三角尺、量角器、圆规等.
如果只有圆规和没有刻度的直尺,还能作出符合条件的几何图形吗?
尺规作图的定义:
新知
我们把只能使用圆规和没有刻度的直尺这两种工具作几何图形的方法称为尺规作图.
想一想,学过的几何图形中,哪些可以用尺规作图得到?
作一条线段等于已知线段
如图所示,已知线段DE,作一条线段等于已知线段DE.
作法:如图所示.
第一步:先作射线AB ;
第二步:再用圆规在射线AB上截取AC,使
AC = DE,线段AC就是所要作的线段.
D
E
A
B
C
【例1】如图,已知线段a,b(a>b),求作一条线段AB,使AB = 2(a-b).
例题
a
b
分析: AB = 2(a-b) = 2a-2b,故只需先作2a,再作2b,将2a中和2b重合部分去掉即可.
【例1】如图,已知线段a,b(a>b),求作一条线段AB,使AB = 2(a-b).
a
b
解:如图,
(1)作射线OP;
(2)在射线OP上顺次截取OM = MB = a;
(3)在线段OB上顺次截取ON = NA = b,则线段
AB就是所求作的线段.
A
B
O
P
M
N
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
第一步:作射线O′A′;
第二步:以点O为圆心,以适当长为半径作弧,交OA于点C,交OB于点D;
第三步:以点O′为圆心,以OC长为半径作弧,交O′A′于点C′;
A′
O′
C
D
C′
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
第四步:以点C′为圆心,以CD长为半径作弧,交前一条弧于
点D′;
第五步:经过点D′作射线O′B′,∠A′O′B′就是所求作的角,如图.
A′
C
D
C′
O′
D′
B′
作一个角等于已知角
如图所示,已知∠AOB ,作∠A′O′B′=∠AOB.
A′
C′
O′
C
D
D′
B′
第四步:以点C′为圆心,以CD长为半径作弧,交前一条弧于
点D′;
第五步:经过点D′作射线O′B′,∠A′O′B′就是所求作的角,如图.
思考:为什么作出的角和已知角相等?理论依据是什么?
你知道如何用尺规作图作一个角等于刚刚所作角的二倍吗?
如何作已知角的平分线呢?
作已知角的平分线
如图,∠AOB 为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.
第一步:在射线OA、AB上,分别截取OD、OE.使OD = OE;
第二步:分别以点D和点E为圆心、
适当长(大于线段DE长的一半)为
半径作圆弧,在∠AOB内,两弧
交于点C;
A
O
C
E
D
B
作已知角的平分线
如图,∠AOB 为已知角,试按下列步骤用直尺和圆规准确地作出∠AOB的平分线.
第三步:作射线OC.
射线OC就是所要求作的∠AOB的平分线.
A
O
E
D
B
如何证明OC是∠AOB的平分线?
C
如图,连结EC、DC .
∵OD = OE,DC = EC,OC = OC,
∴△OCD≌△OCE(S.S.S.),
∴∠AOC =∠BOC (全等三角形的对应
角相等).
为简化推理格式,今后只注明主要依据,省略“已知”、“等量代换” 等依据.
1.如图,用尺规作图:“过点C作CN∥OA”,其作图依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角相等,两直线平行
D.同旁内角互补,两直线平行
练习
B
S.S.S.
3.如图,已知∠AOB和线段PQ,利用“同位角相等,两直线平行”用尺规作图:“过点C作CN∥OA”,并作∠BCN的平分线,截取
CM = PQ.(保留作图痕迹)
练习
A
O
C
B
N
M
Q
P
.
本节课学习了哪些内容?
1.什么是尺规作图:
我们把只能使用圆规和没有刻度的直尺这两种工具作几何图形的方法称为尺规作图.
2. 尺规的基本作图:
①作一条线段等于已知线段;
②作一个角等于已知角;
③作已知角的平分线.
课堂小结
