人教版数学九年级上册 23.3课题学习 图案设计教案(表格式)
文档属性
| 名称 | 人教版数学九年级上册 23.3课题学习 图案设计教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 586.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 00:00:00 | ||
图片预览




文档简介
23.3 课题学习 图案设计
课题 23.3 课题学习 图案设计 授课人
教 学 目 标 知识技能 1.认识和欣赏平移、旋转、轴对称变换在现实生活中的应用; 2.能够灵活运用平移、旋转、轴对称变换进行简单的图案设计.
数学思考 通过学生操作和试验,构建自主学习环境,充分发挥学生的主动性,让学生在活动中获取知识.
问题解决 经历搜集、欣赏、分析、设计和操作的过程,培养学生搜集和整理信息的能力,分析和解决问题的能力,合作和交流的能力以及创新能力.
情感态度 经历对典型图案设计意图的分析,进一步发展学生的空间观念,增强审美意识.
教学重点 利用各种图形变换设计组合图案.
教学难点 将基本图形创造性地运用平移、旋转、轴对称变换设计出丰富、美观的组合图案.
授课类型 新授课 课时
教具 多媒体
教学活动
教学步骤 师生活动 设计意图
回顾 回顾以下问题: 1.平移、旋转和轴对称变换的基本特征; 2.归纳三种图形变换的共性; 3.图片欣赏:利用多媒体演示三种图形变换. 师生活动:学生思考交流后回答,教师进行点评和归纳. 用美丽的图片捕捉学生的眼睛,帮助学生回顾三种图形变换.
活动 一: 创设 情境 导入 新课 【课堂引入】 展示问题:观察图23-3-6,分析它是将哪个基本图形经过了哪些变换后得到的,你能用平移、旋转或轴对称变换分析这个图案的形成过程吗? 图23-3-6 师生活动:学生观察图形,将基本图形从组合图案中分离出来.教师利用多媒体演示基本图形经过三种变换后得到组合图案的过程,突出基本图形经过不同的图形变换后得到组合图案的过程. 通过辨析图形,认识图形变换的本质,让学生感受数学的生动、灵活、美感,调动学生的创作热情.
活动 二: 实践 探究 交流 新知 1.探究新知 活动一:学生展示搜集到的利用平移、旋转和轴对称变换设计的组合图案. 学生在展示的同时,说明组合图案是运用了哪种图形变换得到的,最基本的图形是什么. 教师观察学生的展示,适时评价或肯定. 活动二:教师引导学生反思图案设计的关键. 学生讨论后,师生进行总结: 选取简单的基本几何图形,通过不同的变换组合出丰富的图案. 即时小练:如图23-3-7所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的是( B ) 图23-3-7 图23-3-8 2.综合运用 教师指导学生选择简单的基本图形,进行不同的图形变换,组合出美丽的图案.如利用三角形、矩形、菱形、圆等基本图形,进行图案设计. 学生活动:自己独立设计;小组交流设计图案;小组内选出优秀图案班内展示. 教师活动:组织学生进行评价选择. 1.对学生进行创新意识的培养,让学生在合作中学习与他人交流,集思广益. 2.以学生为主展示其创作成果,在促进学生进行数学交流的基础上增强其表达与交流的意识.
活动 三: 开放 训练 体现 应用 【应用举例】 例1 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( C ) 图23-3-9 例2 如图23-3-10,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程: 答案不唯一,如△ABC向上平移4个单位,再沿y轴对折,得到△DEF . 图23-3-10 师生活动:学生解答问题,教师进行个别提问,最后总结解题方法. 典型问题的设计考查学生对于基础知识的理解和运用.
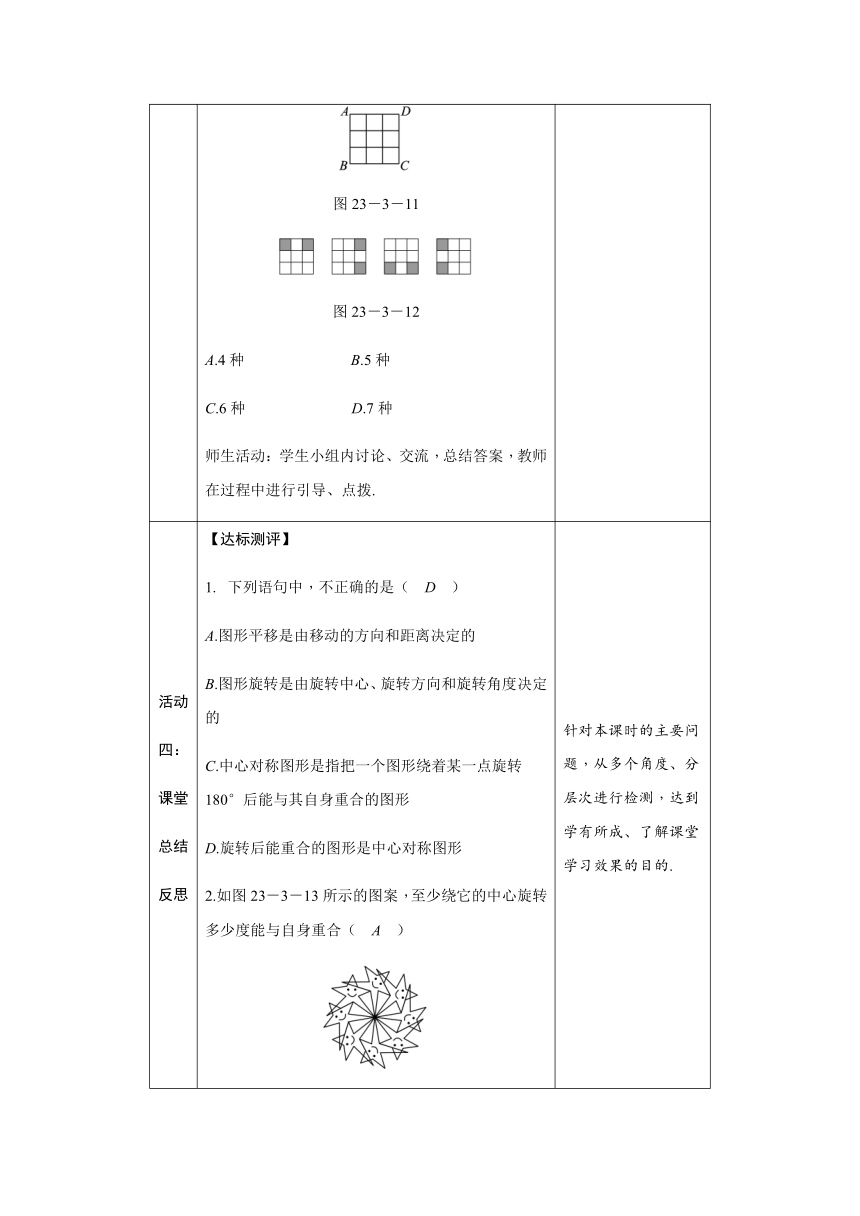
【拓展提升】 图23-3-11是3×3的正方形网格,将其中两个正方形涂灰,并且使得涂灰后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种,图23-3-12中的四幅图就视为同一种,则得到的不同图案共有( C ) 图23-3-11 图23-3-12 A.4种 B.5种 C.6种 D.7种 师生活动:学生小组内讨论、交流,总结答案,教师在过程中进行引导、点拨. 设置开放型问题利于激发学生的思维,拓展学生的思维空间,发挥学生的想象力.
活动 四: 课堂 总结 反思 【达标测评】 下列语句中,不正确的是( D ) A.图形平移是由移动的方向和距离决定的 B.图形旋转是由旋转中心、旋转方向和旋转角度决定的 C.中心对称图形是指把一个图形绕着某一点旋转180°后能与其自身重合的图形 D.旋转后能重合的图形是中心对称图形 2.如图23-3-13所示的图案,至少绕它的中心旋转多少度能与自身重合( A ) 图23-3-13 A.45° B.90° C.135° D.180° 3.如图23-3-14,这些美丽的图案都是在几何画板软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的基本图案绕着它的旋转中心旋转同样的角度得来的,则旋转的角度为( C ) 图23-3-14 A.30° B.60° C.90° D.180° 4.如图23-3-15,图①经过 轴对称 变换得到图②;图①经过 旋转 变换得到图③;图①经过 平移 变换得到图④.(填“平移”“旋转”或“轴对称”) 图23-3-15 如图23-3-16,以点O为旋转中心,将阴影图形顺时针旋转90°三次,作出旋转后的图形. 图23-3-16 学生进行当堂检测,完成后,教师进行批阅、点评、讲解. 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结: (1)你在本节课的学习中有哪些收获?哪些进步? (2)学习完本节课后,你还存在哪些困惑? 2.布置作业: 教材第76页复习题23第4,5,6,8题. 让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】 提纲挈领,重点突出.
【教学反思】 ①[授课流程反思] 在教学过程中,注重引导学生动手实践,以创造性地运用数学知识进行图案设计为主线,增强学生学好数学的信念,更好地提高学生的动手操作能力和实践能力. ②[讲授效果反思] 教师引导学生注意灵活运用图形变换方式,将基本图形进行变换. ③[师生互动反思] 从课堂表现和学生表现分析,学生能够充分发挥主观能动性,创造性地进行图案设计,较好地完成学习任务. ④[习题反思] 好题题号 错题题号 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
学习目标
1.认识和欣赏平移、轴对称、旋转在现实生活中的应用.
2. 利用图形的平移、轴对称、旋转变换设计组合图案.
重点难点
重点:设计图案.
难点:如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
预习导学
一、自学指导.(10分钟)
自学:自学教材P72内容,思考下列问题.
(1)我们学过哪些图形变换?它们分别有何特征?
(2)下列图形之间的变换分别属于什么变换?
探究:
(1)观察下面的图形,分析它是将哪种基本图形经过了哪些变换后得到的?
(2)观察三种图形变换的过程,回答问题:
①平移、旋转和轴对称变换的基本特征;
②归纳三种图形变换的共性.
二、自学检测:学生自主完成,小组内展示,点评,教师巡视.(8分钟)
1.分析图案的形成过程要注意些什么?
分析图案的形成过程,应注意运用__平移、__轴对称__、__旋转__进行描述,只要合理就行.
2.图案设计的关键是什么?
选取简单的基本几何图形,然后通过不同的变换组合出美丽的图案.
合作探究
一、小组合作:小组讨论交流解题思路,小组活动后,小组代表展示活动成果.(7分钟)
用平移、旋转或轴对称变换分析下图中各个图案,分析它是将哪种基本图形经过了哪些变换后得到的?
点拨精讲:将基本图形从组合图案中分离出来,并再现此基本图形的变换过程.
二、跟踪练习:学生独立确定解题思路,小组内交流,上台展示并讲解思路.(8分钟)
1.某单位搞绿化,要在一块圆形空地上种植四种颜色的花,为了便于管理和美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,你能帮忙设计吗?
点拨精讲:将基本图形创造性地应用平移、轴对称、旋转等变换,设计出和谐、丰富、美观的组合图案.
2.下面花边中的图案,由圆弧、圆构成.仿照例图,请你为班级的板报设计一条花边,要求:
(1)只要画出组成花边的一个图案;
(2)以所给的图形为基础,用圆弧、圆或线段画出;
(3)图案应有美感.
课堂小结
学生总结本堂课的收获与困惑.(2分钟)
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
当堂训练
请使用本课时对应训练部分.(10分钟)
课题 23.3 课题学习 图案设计 授课人
教 学 目 标 知识技能 1.认识和欣赏平移、旋转、轴对称变换在现实生活中的应用; 2.能够灵活运用平移、旋转、轴对称变换进行简单的图案设计.
数学思考 通过学生操作和试验,构建自主学习环境,充分发挥学生的主动性,让学生在活动中获取知识.
问题解决 经历搜集、欣赏、分析、设计和操作的过程,培养学生搜集和整理信息的能力,分析和解决问题的能力,合作和交流的能力以及创新能力.
情感态度 经历对典型图案设计意图的分析,进一步发展学生的空间观念,增强审美意识.
教学重点 利用各种图形变换设计组合图案.
教学难点 将基本图形创造性地运用平移、旋转、轴对称变换设计出丰富、美观的组合图案.
授课类型 新授课 课时
教具 多媒体
教学活动
教学步骤 师生活动 设计意图
回顾 回顾以下问题: 1.平移、旋转和轴对称变换的基本特征; 2.归纳三种图形变换的共性; 3.图片欣赏:利用多媒体演示三种图形变换. 师生活动:学生思考交流后回答,教师进行点评和归纳. 用美丽的图片捕捉学生的眼睛,帮助学生回顾三种图形变换.
活动 一: 创设 情境 导入 新课 【课堂引入】 展示问题:观察图23-3-6,分析它是将哪个基本图形经过了哪些变换后得到的,你能用平移、旋转或轴对称变换分析这个图案的形成过程吗? 图23-3-6 师生活动:学生观察图形,将基本图形从组合图案中分离出来.教师利用多媒体演示基本图形经过三种变换后得到组合图案的过程,突出基本图形经过不同的图形变换后得到组合图案的过程. 通过辨析图形,认识图形变换的本质,让学生感受数学的生动、灵活、美感,调动学生的创作热情.
活动 二: 实践 探究 交流 新知 1.探究新知 活动一:学生展示搜集到的利用平移、旋转和轴对称变换设计的组合图案. 学生在展示的同时,说明组合图案是运用了哪种图形变换得到的,最基本的图形是什么. 教师观察学生的展示,适时评价或肯定. 活动二:教师引导学生反思图案设计的关键. 学生讨论后,师生进行总结: 选取简单的基本几何图形,通过不同的变换组合出丰富的图案. 即时小练:如图23-3-7所示的图案是由六个全等的菱形拼成的,它也可以看作是以一个图案为“基本图案”,通过旋转得到的.以下图案中,不能作为“基本图案”的是( B ) 图23-3-7 图23-3-8 2.综合运用 教师指导学生选择简单的基本图形,进行不同的图形变换,组合出美丽的图案.如利用三角形、矩形、菱形、圆等基本图形,进行图案设计. 学生活动:自己独立设计;小组交流设计图案;小组内选出优秀图案班内展示. 教师活动:组织学生进行评价选择. 1.对学生进行创新意识的培养,让学生在合作中学习与他人交流,集思广益. 2.以学生为主展示其创作成果,在促进学生进行数学交流的基础上增强其表达与交流的意识.
活动 三: 开放 训练 体现 应用 【应用举例】 例1 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( C ) 图23-3-9 例2 如图23-3-10,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程: 答案不唯一,如△ABC向上平移4个单位,再沿y轴对折,得到△DEF . 图23-3-10 师生活动:学生解答问题,教师进行个别提问,最后总结解题方法. 典型问题的设计考查学生对于基础知识的理解和运用.
【拓展提升】 图23-3-11是3×3的正方形网格,将其中两个正方形涂灰,并且使得涂灰后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种,图23-3-12中的四幅图就视为同一种,则得到的不同图案共有( C ) 图23-3-11 图23-3-12 A.4种 B.5种 C.6种 D.7种 师生活动:学生小组内讨论、交流,总结答案,教师在过程中进行引导、点拨. 设置开放型问题利于激发学生的思维,拓展学生的思维空间,发挥学生的想象力.
活动 四: 课堂 总结 反思 【达标测评】 下列语句中,不正确的是( D ) A.图形平移是由移动的方向和距离决定的 B.图形旋转是由旋转中心、旋转方向和旋转角度决定的 C.中心对称图形是指把一个图形绕着某一点旋转180°后能与其自身重合的图形 D.旋转后能重合的图形是中心对称图形 2.如图23-3-13所示的图案,至少绕它的中心旋转多少度能与自身重合( A ) 图23-3-13 A.45° B.90° C.135° D.180° 3.如图23-3-14,这些美丽的图案都是在几何画板软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的基本图案绕着它的旋转中心旋转同样的角度得来的,则旋转的角度为( C ) 图23-3-14 A.30° B.60° C.90° D.180° 4.如图23-3-15,图①经过 轴对称 变换得到图②;图①经过 旋转 变换得到图③;图①经过 平移 变换得到图④.(填“平移”“旋转”或“轴对称”) 图23-3-15 如图23-3-16,以点O为旋转中心,将阴影图形顺时针旋转90°三次,作出旋转后的图形. 图23-3-16 学生进行当堂检测,完成后,教师进行批阅、点评、讲解. 针对本课时的主要问题,从多个角度、分层次进行检测,达到学有所成、了解课堂学习效果的目的.
1.课堂总结: (1)你在本节课的学习中有哪些收获?哪些进步? (2)学习完本节课后,你还存在哪些困惑? 2.布置作业: 教材第76页复习题23第4,5,6,8题. 让学生养成自主归纳课堂重点的习惯,提高学生的学习能力.
【知识网络】 提纲挈领,重点突出.
【教学反思】 ①[授课流程反思] 在教学过程中,注重引导学生动手实践,以创造性地运用数学知识进行图案设计为主线,增强学生学好数学的信念,更好地提高学生的动手操作能力和实践能力. ②[讲授效果反思] 教师引导学生注意灵活运用图形变换方式,将基本图形进行变换. ③[师生互动反思] 从课堂表现和学生表现分析,学生能够充分发挥主观能动性,创造性地进行图案设计,较好地完成学习任务. ④[习题反思] 好题题号 错题题号 反思教学过程和教师表现,进一步优化操作流程和提升自身素质.
学习目标
1.认识和欣赏平移、轴对称、旋转在现实生活中的应用.
2. 利用图形的平移、轴对称、旋转变换设计组合图案.
重点难点
重点:设计图案.
难点:如何利用平移、轴对称、旋转等图形变换中的一种或它们的组合得出图案.
预习导学
一、自学指导.(10分钟)
自学:自学教材P72内容,思考下列问题.
(1)我们学过哪些图形变换?它们分别有何特征?
(2)下列图形之间的变换分别属于什么变换?
探究:
(1)观察下面的图形,分析它是将哪种基本图形经过了哪些变换后得到的?
(2)观察三种图形变换的过程,回答问题:
①平移、旋转和轴对称变换的基本特征;
②归纳三种图形变换的共性.
二、自学检测:学生自主完成,小组内展示,点评,教师巡视.(8分钟)
1.分析图案的形成过程要注意些什么?
分析图案的形成过程,应注意运用__平移、__轴对称__、__旋转__进行描述,只要合理就行.
2.图案设计的关键是什么?
选取简单的基本几何图形,然后通过不同的变换组合出美丽的图案.
合作探究
一、小组合作:小组讨论交流解题思路,小组活动后,小组代表展示活动成果.(7分钟)
用平移、旋转或轴对称变换分析下图中各个图案,分析它是将哪种基本图形经过了哪些变换后得到的?
点拨精讲:将基本图形从组合图案中分离出来,并再现此基本图形的变换过程.
二、跟踪练习:学生独立确定解题思路,小组内交流,上台展示并讲解思路.(8分钟)
1.某单位搞绿化,要在一块圆形空地上种植四种颜色的花,为了便于管理和美观,相同颜色的花集中种植,且每种颜色的花所占的面积相同,现征集设计方案,你能帮忙设计吗?
点拨精讲:将基本图形创造性地应用平移、轴对称、旋转等变换,设计出和谐、丰富、美观的组合图案.
2.下面花边中的图案,由圆弧、圆构成.仿照例图,请你为班级的板报设计一条花边,要求:
(1)只要画出组成花边的一个图案;
(2)以所给的图形为基础,用圆弧、圆或线段画出;
(3)图案应有美感.
课堂小结
学生总结本堂课的收获与困惑.(2分钟)
利用平移、轴对称和旋转的图形变换中的一种或组合设计图案.
当堂训练
请使用本课时对应训练部分.(10分钟)
同课章节目录
