人教版数学八年级上册 13.1.2.1 线段的垂直平分线的性质和判定 课件(共24张PPT)
文档属性
| 名称 | 人教版数学八年级上册 13.1.2.1 线段的垂直平分线的性质和判定 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 601.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 10:39:42 | ||
图片预览




文档简介
(共24张PPT)
第十三章 轴对称
13.1.2.1 线段的垂直平分线的性质和判定
1、理解线段垂直平分线的性质和判定。
2、能运用线段垂直平分线的性质和判定解决实际问题。
3、会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理。
学 习 目 标
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
对折
完全重合
复 习 导 入
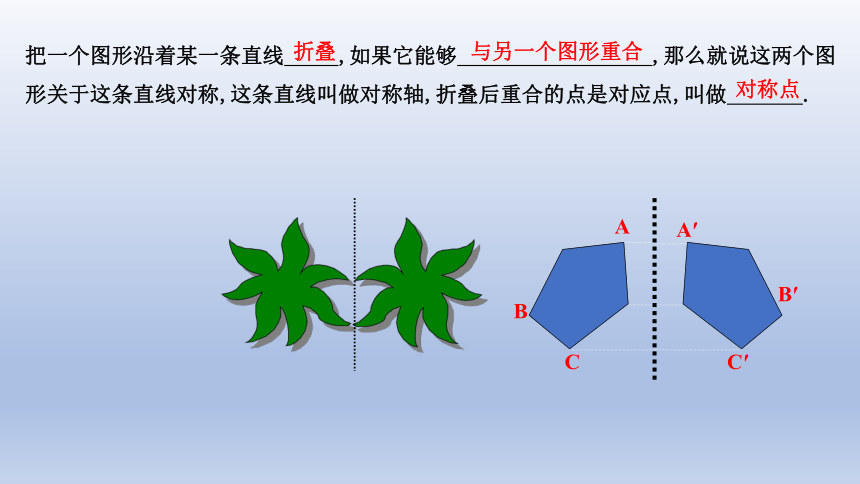
把一个图形沿着某一条直线 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
折叠
与另一个图形重合
对称点
A′
A
B
C
B′
C′
D
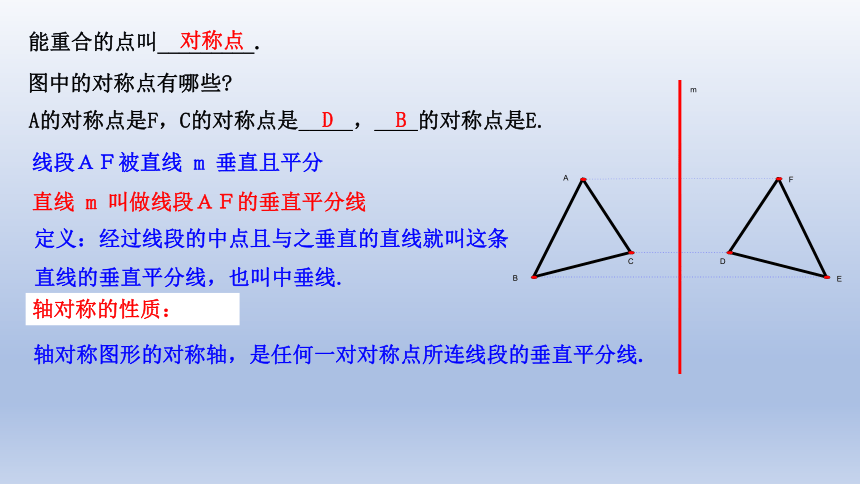
A的对称点是F,C的对称点是_____,____的对称点是E.
能重合的点叫_________.
对称点
图中的对称点有哪些
B
线段AF被直线 m 垂直且平分
直线 m 叫做线段AF的垂直平分线
定义:经过线段的中点且与之垂直的直线就叫这条直线的垂直平分线,也叫中垂线.
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称的性质:
探究 1 线段的垂直平分线的性质
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
合 作 探 究
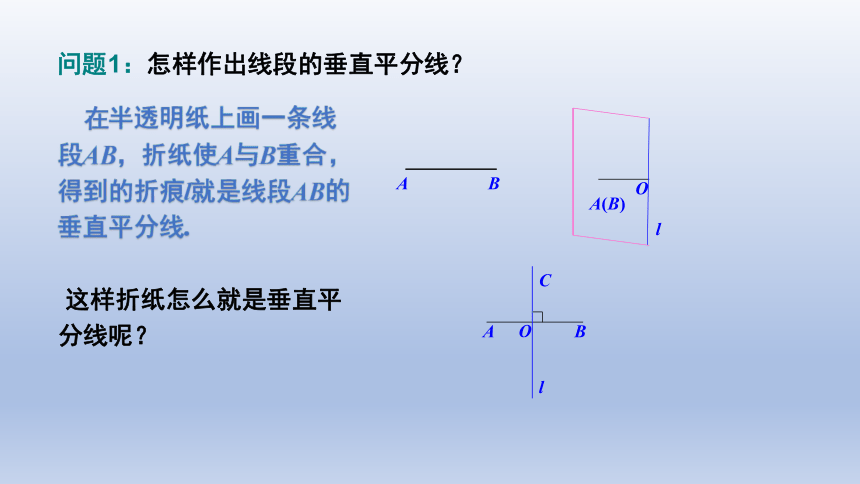
问题1:怎样作出线段的垂直平分线?
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
这样折纸怎么就是垂直平分线呢?
A
B
A(B)
A
B
l
O
l
C
O
A
B
C
D
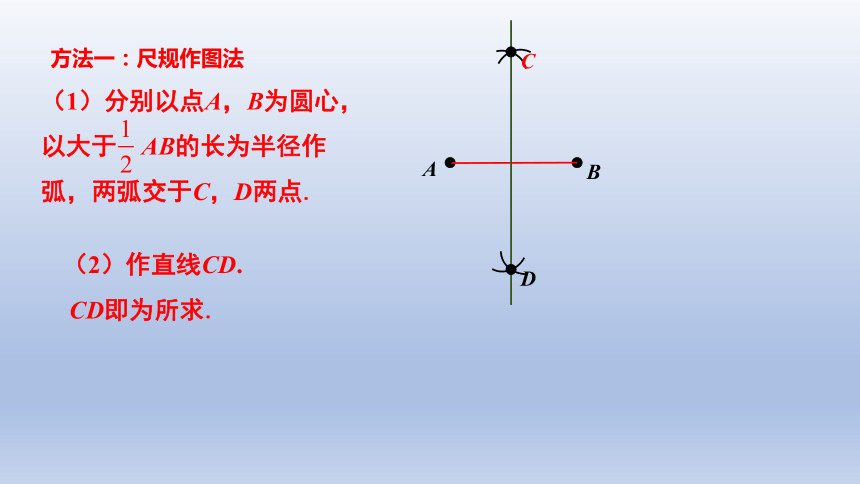
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
方法一:尺规作图法
使线段AA'的两个端点互相重合,
A’
A
(A')
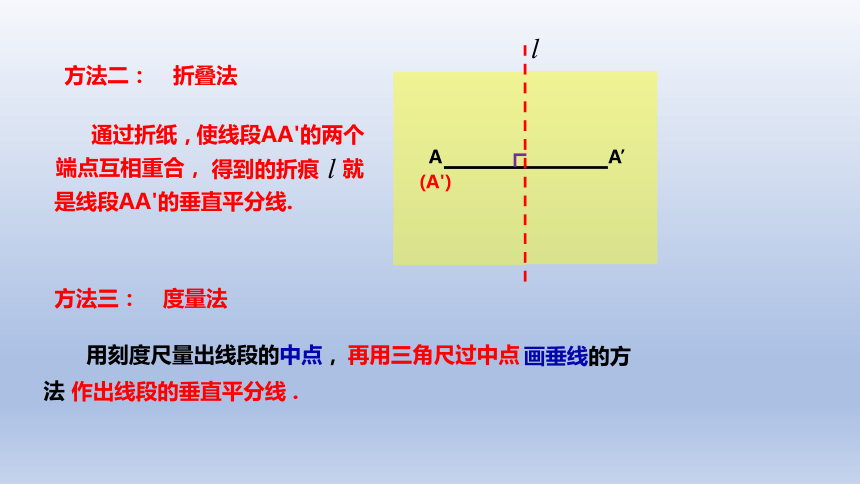
折叠法
方法二:
就是线段AA'的垂直平分线.
通过折纸,
得到的折痕
画垂线的方法
度量法
方法三:
用刻度尺量出线段的中点,
再用三角尺过中点
作出线段的垂直平分线 .
问题2:
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
A
B
l
P1
P2
P3
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
A
B
P
C
l
证明:
∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS)
∴ PA =PB.
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
M
N
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴ PA=PB
新 知 小 结
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴BD=AD
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
典 例 精 析
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段两端的距离相等。反过来,如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗?
A
B
Q
A
B
Q
情况一
点在线段上
情况二
点在线段外
探究 2 线段的垂直平分线的判定
A
B
Q
问题1:点在线段上
若点Q在线段AB上,且QA=QB,
则Q是线段AB的中点,
点Q在线段AB的垂直平分线上。
问题2:点在线段外
A
B
Q
如图,若点Q在线段AB外,且QA=QB,则作QM⊥AB,垂足为M。
M
证明:
∵ QM⊥AB,
∴ ∠PMA =∠PMB=90°.
在Rt△QAM和Rt△QBM中
∵ AQ =QB,QM =QM,
∴ Rt△QAM ≌Rt△QBM( HL) ∴ AM =BM.
即点Q在线段AB的垂直平分线上
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB两端点距离相等的点?
与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与A、B两点的距离相等的所有点的集合.
P
A
B
C
l
思 考
A
B
P
C
l
到线段两个端点的距离相等的点在线段垂直平分线上。
几何语言描述:
∵PA=PB
∴点P在线段AB的垂直平分线上
线段的垂直平分线是到线段两端距离相等的点的集合。
新 知 小 结
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
典 例 精 析
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
随 堂 练 习
3.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
4.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E . 求证:直线AD是CE的垂直平分线.
证明:
∵ AD平分∠BAC
∴ ∠EAD=∠CAD
∵ ∠ACB=90°,DE⊥AB
∴ ∠AED=∠ACB=90°
在 △AED 和 △FCE 中
∵
(公共边)
AD=AD
∠AED=∠ACB
∠EAD=∠CAD
∴ △ADE≌△ADC
∴ AE=AC,
∴ 点A、D都在CE的垂直平分线上
DE=DC
∴ 直线AD是CE的垂直平分线
(AAS)
到线段两端的距离相等.
线段垂直平分线上的点
① 性质定理:
A
B
P
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
到线段两端距离相等的点
在线段的垂直平分线上.
② 判定定理:
线段的垂直平分线
作用:判断一个点是否在线段的垂直平分线上.
这点到三角形三个顶点的距离相等.
三角形三边的垂直平分线相交于一点,
必须证明这条直线上有两点到线段两端的距离相等
利用判定定理证一条直线是线段的垂直平分线,
④方法技巧:
( 即证有两点在线段的垂直平分线上 ).
③结论:
课 堂 总 结
第十三章 轴对称
13.1.2.1 线段的垂直平分线的性质和判定
1、理解线段垂直平分线的性质和判定。
2、能运用线段垂直平分线的性质和判定解决实际问题。
3、会用尺规经过已知直线外一点作这条直线的垂线,了解作图的道理。
学 习 目 标
如果一个图形沿着一条直线 ,两侧的图形能够 ,这个图形就是轴对称图形.
折痕所在的这条直线叫做_________.
对称轴
对折
完全重合
复 习 导 入
把一个图形沿着某一条直线 ,如果它能够 ,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做 .
折叠
与另一个图形重合
对称点
A′
A
B
C
B′
C′
D
A的对称点是F,C的对称点是_____,____的对称点是E.
能重合的点叫_________.
对称点
图中的对称点有哪些
B
线段AF被直线 m 垂直且平分
直线 m 叫做线段AF的垂直平分线
定义:经过线段的中点且与之垂直的直线就叫这条直线的垂直平分线,也叫中垂线.
轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线.
轴对称的性质:
探究 1 线段的垂直平分线的性质
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
合 作 探 究
问题1:怎样作出线段的垂直平分线?
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
这样折纸怎么就是垂直平分线呢?
A
B
A(B)
A
B
l
O
l
C
O
A
B
C
D
(1)分别以点A,B为圆心,以大于 AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
方法一:尺规作图法
使线段AA'的两个端点互相重合,
A’
A
(A')
折叠法
方法二:
就是线段AA'的垂直平分线.
通过折纸,
得到的折痕
画垂线的方法
度量法
方法三:
用刻度尺量出线段的中点,
再用三角尺过中点
作出线段的垂直平分线 .
问题2:
如图,直线l垂直平分线段AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
A
B
l
P1
P2
P3
猜想:
点P1,P2,P3,… 到点A 与点B 的距离分别相等.
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论?
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l 上.
求证:PA =PB.
A
B
P
C
l
证明:
∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS)
∴ PA =PB.
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
M
N
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴ PA=PB
新 知 小 结
D
C
B
E
A
解:
∵ED是线段AB的垂直平分线
∴BD=AD
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=AD+DC+BC
=AC+BC
=12+7=19
如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
典 例 精 析
如果一个点在一条线段的垂直平分线上,那么这个点到这条线段两端的距离相等。反过来,如果一个点到一条线段两端的距离相等,那么这个点在这条线段的垂直平分线上吗?
A
B
Q
A
B
Q
情况一
点在线段上
情况二
点在线段外
探究 2 线段的垂直平分线的判定
A
B
Q
问题1:点在线段上
若点Q在线段AB上,且QA=QB,
则Q是线段AB的中点,
点Q在线段AB的垂直平分线上。
问题2:点在线段外
A
B
Q
如图,若点Q在线段AB外,且QA=QB,则作QM⊥AB,垂足为M。
M
证明:
∵ QM⊥AB,
∴ ∠PMA =∠PMB=90°.
在Rt△QAM和Rt△QBM中
∵ AQ =QB,QM =QM,
∴ Rt△QAM ≌Rt△QBM( HL) ∴ AM =BM.
即点Q在线段AB的垂直平分线上
这些点能组成什么几何图形?
你能再找一些到线段AB 两端点的距离相等的点吗?能找到多少个到线段AB两端点距离相等的点?
与A,B 的距离相等的点都在直线l上,所以直线l 可以看成与A、B两点的距离相等的所有点的集合.
P
A
B
C
l
思 考
A
B
P
C
l
到线段两个端点的距离相等的点在线段垂直平分线上。
几何语言描述:
∵PA=PB
∴点P在线段AB的垂直平分线上
线段的垂直平分线是到线段两端距离相等的点的集合。
新 知 小 结
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D,连接CD.求证:OE是CD的垂直平分线.
典 例 精 析
1.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A. 6 B. 5 C. 4 D. 3
2.如图②所示,在△ABC中,BC=8cm,边AB的垂直平分线交AB于点D,交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
B
10cm
P
A
B
C
D
图①
A
B
C
D
E
图②
随 堂 练 习
3.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB .
A
B
C
D
A
4.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC ( )
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
5.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E . 求证:直线AD是CE的垂直平分线.
证明:
∵ AD平分∠BAC
∴ ∠EAD=∠CAD
∵ ∠ACB=90°,DE⊥AB
∴ ∠AED=∠ACB=90°
在 △AED 和 △FCE 中
∵
(公共边)
AD=AD
∠AED=∠ACB
∠EAD=∠CAD
∴ △ADE≌△ADC
∴ AE=AC,
∴ 点A、D都在CE的垂直平分线上
DE=DC
∴ 直线AD是CE的垂直平分线
(AAS)
到线段两端的距离相等.
线段垂直平分线上的点
① 性质定理:
A
B
P
PA=PB
点P在线段AB的垂直平分线上
到线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
到线段两端距离相等的点
在线段的垂直平分线上.
② 判定定理:
线段的垂直平分线
作用:判断一个点是否在线段的垂直平分线上.
这点到三角形三个顶点的距离相等.
三角形三边的垂直平分线相交于一点,
必须证明这条直线上有两点到线段两端的距离相等
利用判定定理证一条直线是线段的垂直平分线,
④方法技巧:
( 即证有两点在线段的垂直平分线上 ).
③结论:
课 堂 总 结
