§30.3.1借助调查作决策(2)(四川省达川地区达县)
文档属性
| 名称 | §30.3.1借助调查作决策(2)(四川省达川地区达县) |  | |
| 格式 | rar | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-01-29 19:39:00 | ||
图片预览











文档简介
课件31张PPT。§30.3.1借助调查作决策(2)迎着初升的太阳一起出发1.这样问好吗?一.问题引入同学们,当你遇到以下问题时,你怎么
办呢?
(1)学校里要组织运动会,哪些项目更受欢迎?
(2)顾客对电器公司售后服务的满意程度如何?
(3)一碗汤的咸淡如何?(必须自已展开调查才能获得需要的信息)二、回顾根据你以前所学的知识,想一想应如何
通过调查收集数据?需要经过哪些步骤?
(一般可通过民意调查、实地调查、媒体
调查等来收集数据;需要经过明确调查问题
确定调查对象、选择调查方法、展开调查、
记录结果、得出结论六个步骤。)提出问题分析数据收集数据整理数据作出决策被调查对象的答案
必须具有:针对性、
真实性、
确定性
设计调查问题 设计调查方法抽样普查民意调查、媒体调查、
实地(亲自)调查法统计图表统计表、条形统计图、
折线统计图、扇形统计图
特征数据集中程度:
平均数、中位数、众数离散程度:
极差、方差、标准差理论服务于实践三、共同解决问题,领会新知 厂家为了了解客户的意见和需求,可事先拟定一份调查问卷,再用简单的随机抽样方法在所有客户中选取一部分进行调查,打电话或发放问卷等,这些都是很常见的调查方式。但是很多时候怎样问问题,怎样整理数据,并不如想像中那样轻而易举。 请看问题“这样问好吗?”
问题:“你是一个计算机用户吗?”这是一项调查中的一个问题。下面是几位被调查者的回答:
A:是(因为他使用过一次计算机)
B:否(因为她不是经常使用计算机)
C:否(因为他只用计算机打游戏)
D:是(因为她在超市从事收银工作)
从中你发现这个问题有什么不妥?你打算如何修改?师:这个问题问得不明确,不同的人可能有不同的理解,所发应该根据抽查目的重设计问题,如“你每天使用计算机吗?”“你使用计算机主要做什么?”这样问好吗?你是一个计算机用户吗?
(意义不明确)
您觉得我厂食品是否美味价廉?
(问题重叠)
你对数学老师的教学满意吗?
(缺乏程度区分)
你是否有过考试作弊的行为?
(需要考虑答案的真实性)1.磨刀小试:以下调查问题有何不妥? 例1、某品牌的洗衣机生产厂家为了了解顾客对该品牌洗衣机的满意程度,在洗衣机的使用说明手册中附上了一份意见表.表上有这样一段文字:计算出该品牌洗衣机的顾客满意率.2、亲身体验,形成观念如果您对本产品不满意,请在下表中填上“不满意”,然后将此表寄回本厂服务部.本厂通讯地址为:××省××市×××路××号,邮编:××××××. 该厂服务部根据回信统计出对产品不满意的顾客数,再从厂家销售部获知该品牌洗衣机的销售量,利用公式“
对疹下药,皆大欢喜调查表设计成明信片的便利措施、用礼品增强吸引力顾客至上,客户回访……回顾与反思:
(1)调查首先应制订合适的调查方案,而这需要我们去精心设计.方案的设计可谓“失之毫厘,差之千里”.
(2)调查时究竟是采用“普查”还是“抽样调查”方式进行需要根据实际情况而定,而用样本估算总体的统计思想方法则是一种较简便、实用的统计方法.希望同学们通过实践操作逐步提高这方面的能力.2.怎样整理好数据 看球赛时会推测自己喜爱的球队或球星是否会赢,如果这时仅仅依靠主观喜好去作出判断,那就往往不具备统计观念,并且所作的判断往往是不合理的。
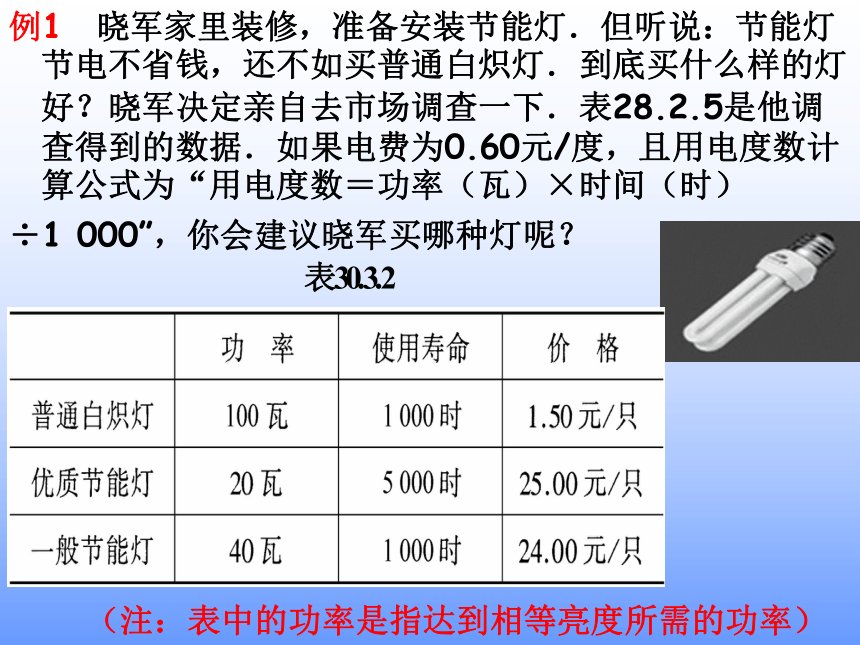
因此,判断前需要先收集一定的数据——双方队员的技术、双方球队历次比赛的成绩记录等,对这些数据进行适当的整理和分析,有了概括的了解后,再对球队的输赢作出推断是比较可靠的。数据的整理例1 晓军家里装修,准备安装节能灯.但听说:节能灯节电不省钱,还不如买普通白炽灯.到底买什么样的灯好?晓军决定亲自去市场调查一下.表28.2.5是他调查得到的数据.如果电费为0.60元/度,且用电度数计算公式为“用电度数=功率(瓦)×时间(时)
÷1 000”,你会建议晓军买哪种灯呢?(注:表中的功率是指达到相等亮度所需的功率)下面是晓军的分析:
计算各种灯使用5 000小时的花费情况,如表30.3.3所示.从上面的计算可以看出: 优质节能灯既节电又省钱.你觉得他的分析有道理吗?例2.某园林的门票每张10元(一次使用),考虑到人们的不同需求,也为了吸引更多的游客,该园林除了保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购票日起,可共持票者使用一年).年票分A、B、C三大类:A类年票每张120元,持票者进入园林时,无需再买门票;B类年票每张60元,持票者进入园林时,需再购门票,每次2元;C类年票每张40元,持票者进入园林时,需再购门票,每次3元.
(1)如果你只选择一种购买门票的方式,并且你计划在一年中用80元花在该园林的门票上,试通过计算,找出可使进入该园林的次数最多的购票方式;
(2)求一年中进入该园林至少超过多少次时,购买A类年票最合算.
分析:由题意可知,一共有四种购票方式.我们要作出决策,关键看一年所花门票费用与进入该园林的次数这两个量.
(1)只需对照每种购票方式,分别计算花80元能进入该园林的次数;
(2)显然,当进入该园林的次数较多时,选择购买A类年票较合算.那么“多”的标准究竟是多少呢?我们只需要分别计算出根据另三种方式花120元能进入该园林的最多次数即可.
解:(略)复习引入1.在一次中考模拟考试中,某校初三(1)班、初三(2)班两班学生数学成绩统计如下表:请你从平均数的角度判断,这两个班的考试成绩谁优谁次。
同学们,你们可曾接触过体育彩票?体育彩票的返奖率为55%.换句话说,平均每销售100元,将会有55元作为奖金奖励给购买体育彩票者中的幸运者(即中奖者),而另外的45元则用于支援国家或地方的体育事业的发展及销售体育彩票的成本费用.
对于55%的返奖率这一数据,能否理解为购买平均100张体育彩票就有55张中奖呢?从你接触到的人群中了解到的信息,中奖面有这么大吗?那么,到底平均要买几张才能得奖呢?理论数据与实际数据相符吗?如果返奖率确实为55%,而中奖面远远小于55%.请同学们讨论一下,究竟是什么原因造成的这一差异?
本节课,我们再来领略平均数在生活中的应用--2.平均要买几个才能得奖。例3.一家冷饮厂在电视里做广告,说他们厂生产的雪糕在小木棍上印有四种图案,集齐四个不同图案的小木棍就能够拼成一幅图,凭此可以在指定的商店领取一份礼物.假设该厂准备的四种图案的小木棍一样多,而且每支雪糕中夹入哪种图案的小木棍也完全是随机的,那么,平均要买几支雪糕才能得奖呢?
分 析:
如果幸运,也许买四支就能够得奖;但也有可能要买二十多支才得奖.那么平均要买几支才能得奖呢?不妨运用随机数,作模拟实验来解决这个难题.
令这四种图案的小木棍的编号分别为1号、2号、3号和4号.让计算器在1~4的范围每次产生一个随机整数,作为买到的那支雪糕小木棍的编号,记录下每次买到的编号以及每次得奖买了多少支雪糕.表28.3.2是小明10次实验的数据记录.平均要买几个才能获奖因为
所以小明认为大约平均买7支雪糕才能得奖.
思 考
你的实验记录与小明的记录相同吗?如果不相同,是否表明其中有一张记录是假的?你的实验结果与小明的相同吗?如果不相同,你有何建议?实践与探索例4.某啤酒厂推出一种有奖销售方案:该厂在出厂的所有啤酒的瓶盖内分别印上“再”、“来”、“一”、“瓶”、“啤”、“酒”六个字中的一个(文字颜色与啤酒颜色相近,从瓶外无法看清文字),集齐分别印有这六个不同文字的六个啤酒瓶盖就可换取一瓶该品牌的啤酒.假如印有这六个文字的瓶盖个数一样多,而且每瓶啤酒的瓶盖上印有哪个文字也完全是随机的,那么,平均要买多少瓶啤酒才能中奖(奖1瓶啤酒)呢?试通过模拟实验来解决这一问题.
分析:如果幸运的话,买6瓶啤酒也许就能中奖;但也许购买50瓶、100瓶都无法中奖.那么,平均要买多少瓶啤酒才能中奖呢?请你估计一个答案,写在纸上(最后与模拟实验得到的答案作个比较,看看你的估计能力如何).下面我们利用计算器进行模拟实验:让计算器在1~6的范围内每次产生一个随机整数,作为购买到的那瓶啤酒的瓶盖上的文字的代号(1代表“再”、2代表“来”、3代表“一”、4代表“瓶”、5代表“啤”、6代表“酒”),若“中奖”,则一次实验结束,然后进行下一次实验.记录下每次实验得到的相关数据,整理如下:因为,
所以我们可以估计大约平均要购买15瓶啤酒才能中奖.回顾:(1)此题如果要通过纯计算求出“平均要购买几瓶啤酒才能中奖”非常困难,同时我们也不太可能为了解出此题真的去购买啤酒,而利用计算器、通过模拟实验则相对“简单”地求出了答案.
(2)模拟实验前你估计的答案是什么?与现在求得的“大约15瓶”误差大不大?(3)本题的解法是通过实验去估计答案,因此要注意两点:①不同的人得到的答案不一定相同,即使同一个人再进行相同次数的实验答案也不一定相同;②要想答案尽可能准确,我们可以将实验次数尽可能地增加(但也要考虑到有无必要及可能性).因为实验次数充分大时,这个“平均数”将趋于稳定.例5.甲、乙、丙、丁四位小朋友一起做游戏:他们抛掷3枚硬币,若全部正面朝上,则甲胜;若全部反面朝上,则乙胜;若两枚正面朝上一枚反面朝上,则丙胜;若两枚反面朝上一枚正面朝上,则丁胜.将他们的获胜次数记录、统计如下表:当比赛进行到100次时,甲、乙两人连喊“运气不好”,至此游戏结束.
(1)分别计算游戏进行到30次、50次、100次时,甲、乙、丙、丁四位小朋友的获胜率;
(2)甲、乙两人真的是运气不好吗?请你运用所学知识帮助分析他们两人获胜率低的原因.分析:表面上看,抛掷3枚硬币,观察出现正面朝上的枚数共有四种情形,即这个游戏共有四个不同结果,好象比较“公平”. 但事实上,这四个结果是“等可能”的吗?
解:(1)游戏进行到30次、50次、100次时,甲、乙、丙、丁四位小朋友的获胜率如下表所示:(2)甲、乙两人并不真的是运气不好,而是因为这个游戏规则本身制订得并不公平.画出抛掷硬币的树状图(如图30.3.6):从树状图中可以看出:P(全部正面朝上)= P(全部反面朝上)= ;
而P(两枚正面朝上一枚反面朝上)= P(两枚反面朝上一枚正面朝上)= .
因此,按照原来的游戏规则,甲、乙获胜的概率只有丙、丁获胜的概率 的,故游戏不公平.探索: 针对上面的游戏,能否适当调整一下游戏规则,使得游戏对于四位小朋友来说做到公平?试给出两种不同的调整方案.
分析:调整方案关键在于将原规则中的不公平(获胜机会不均等)处去除,从而使得游戏公平.例如以下两种方案:
①实行积分制.甲获胜1次积3分,乙获胜1次积3分,丙获胜1次积1分,丁获胜1次积1分.这样到比赛结束看积分高低定胜负.
②甲与丙合作,乙与丁合作,即4位小朋友分成两个小组进行对抗比赛.按照原先的游戏规则比赛也能保证游戏公平. 回顾与反思 (1)游戏是否公平有时存在一定的隐蔽性,需要我们运用相关数学知识去分析、评判.而画树状图的关键则在于列出所有等可能出现的事件,从而确定各种结果出现的机会.
(2)有了以上的知识储备,现在,你对街头小巷的一些所谓的“公平游戏”会作如何评价?
课内练习与巩固
某商场春节期间进行有奖销售,规定每购买满50元商品可得刮刮卡一张,每张刮刮卡上印有“萬”、“事”、“如”、“意”四个字中的一个字,集齐分别印有“萬”、“事”、“如”、“意”四个字的四张刮刮卡即中奖——换取一张价值20元的购物券或领取一份价值20元的礼品包.假如印有“萬”、“事”、“如”、“意”的刮刮卡的张数一样多,而且每张刮刮卡上印有哪个字也完全是随机的,那么,平均要买满多少元商品才能中奖呢?试通过模拟实验来解决这一问题. 作业 课本P118 习题30.3第1-3题作业设计1.某校初三学生在一次数学测验中,甲、乙两班学生的成绩统计如下:请根据表格提供的信息回答下列问题:
(1)甲班学生成绩的众数为_________分,乙班学生成绩的众数为_________分.从众数看成绩较好的是__________班;
(2)甲班学生成绩的中位数为_________分,乙班学生成绩的中位数为_________分,甲班中成绩在中位数以上(包括中位数)的学生所占的百分比是_________%,乙班中成绩在中位数以上(包括中位数)的学生所占的百分比是_________%.从中位数看成绩较好的__________班;
(3)若成绩在85分以上的为优秀,则甲班的优秀率为_______%,
乙班的优秀率为______%,从优秀率看成绩较好的是__________班.
(4)请你根据题目给出的信息及以上的计算,对甲、乙两班的成绩作出你的综合评价.
2.某电视台综艺节目接到参与节目的热线电话及短信共3000个,现要从中抽取“幸运观众”10名,王蕾同学发了一条短信,那么她成为“幸运观众”的概率为__________.
3.将一副中国象棋的全部棋子装入一纸箱中,将纸箱封好后在其一个面上挖一方形孔,让此孔刚好能通过一枚棋子.小孔朝下,摇动纸箱,使从小孔中掉出一枚棋子.
(1)掉出的棋子是红“车”的概率是______________;
(2)掉出的棋子是“马”的概率是______________;
(3)掉出的棋子是“兵”或“卒”的概率是______________;
(4)掉出的棋子不是“车”、“马”、“炮”的概率是____________;
(5)请通过具体实验操作得出上述事件发生的可能性有多大,然后与你上面所填的概率结果作出比较,如果不相同,是不是“计算”与“实验”中一定有一项存在问题?4.有一种体育彩票,开奖号码为0000000~9999999之间的七位随机数(注:首位可以是0).若你购买到的号码恰好为开奖号码,则中特等奖;若你购买到的号码中连续6位与开奖号码对应相同(而且必须是相同数位,以下要求相同),则中一等奖;连续5位与开奖号码对应相同,则中二等奖;连续4位与开奖号码对应相同,则中三等奖;连续3位与开奖号码对应相同,则中四等奖;连续2位与开奖号码对应相同,则中五等奖.例如:若开奖号码为6579004,而你购买的号码为0079014,由于第3、4、5位号码相同,即连续3位与开奖号码对应相同,因此你中了四等奖.
(1)购买一张体育彩票中奖(等次不限)的机会大约有多大?
(2)试通过模拟实验求出平均要买多少张体育彩票才能中奖?谢谢
办呢?
(1)学校里要组织运动会,哪些项目更受欢迎?
(2)顾客对电器公司售后服务的满意程度如何?
(3)一碗汤的咸淡如何?(必须自已展开调查才能获得需要的信息)二、回顾根据你以前所学的知识,想一想应如何
通过调查收集数据?需要经过哪些步骤?
(一般可通过民意调查、实地调查、媒体
调查等来收集数据;需要经过明确调查问题
确定调查对象、选择调查方法、展开调查、
记录结果、得出结论六个步骤。)提出问题分析数据收集数据整理数据作出决策被调查对象的答案
必须具有:针对性、
真实性、
确定性
设计调查问题 设计调查方法抽样普查民意调查、媒体调查、
实地(亲自)调查法统计图表统计表、条形统计图、
折线统计图、扇形统计图
特征数据集中程度:
平均数、中位数、众数离散程度:
极差、方差、标准差理论服务于实践三、共同解决问题,领会新知 厂家为了了解客户的意见和需求,可事先拟定一份调查问卷,再用简单的随机抽样方法在所有客户中选取一部分进行调查,打电话或发放问卷等,这些都是很常见的调查方式。但是很多时候怎样问问题,怎样整理数据,并不如想像中那样轻而易举。 请看问题“这样问好吗?”
问题:“你是一个计算机用户吗?”这是一项调查中的一个问题。下面是几位被调查者的回答:
A:是(因为他使用过一次计算机)
B:否(因为她不是经常使用计算机)
C:否(因为他只用计算机打游戏)
D:是(因为她在超市从事收银工作)
从中你发现这个问题有什么不妥?你打算如何修改?师:这个问题问得不明确,不同的人可能有不同的理解,所发应该根据抽查目的重设计问题,如“你每天使用计算机吗?”“你使用计算机主要做什么?”这样问好吗?你是一个计算机用户吗?
(意义不明确)
您觉得我厂食品是否美味价廉?
(问题重叠)
你对数学老师的教学满意吗?
(缺乏程度区分)
你是否有过考试作弊的行为?
(需要考虑答案的真实性)1.磨刀小试:以下调查问题有何不妥? 例1、某品牌的洗衣机生产厂家为了了解顾客对该品牌洗衣机的满意程度,在洗衣机的使用说明手册中附上了一份意见表.表上有这样一段文字:计算出该品牌洗衣机的顾客满意率.2、亲身体验,形成观念如果您对本产品不满意,请在下表中填上“不满意”,然后将此表寄回本厂服务部.本厂通讯地址为:××省××市×××路××号,邮编:××××××. 该厂服务部根据回信统计出对产品不满意的顾客数,再从厂家销售部获知该品牌洗衣机的销售量,利用公式“
对疹下药,皆大欢喜调查表设计成明信片的便利措施、用礼品增强吸引力顾客至上,客户回访……回顾与反思:
(1)调查首先应制订合适的调查方案,而这需要我们去精心设计.方案的设计可谓“失之毫厘,差之千里”.
(2)调查时究竟是采用“普查”还是“抽样调查”方式进行需要根据实际情况而定,而用样本估算总体的统计思想方法则是一种较简便、实用的统计方法.希望同学们通过实践操作逐步提高这方面的能力.2.怎样整理好数据 看球赛时会推测自己喜爱的球队或球星是否会赢,如果这时仅仅依靠主观喜好去作出判断,那就往往不具备统计观念,并且所作的判断往往是不合理的。
因此,判断前需要先收集一定的数据——双方队员的技术、双方球队历次比赛的成绩记录等,对这些数据进行适当的整理和分析,有了概括的了解后,再对球队的输赢作出推断是比较可靠的。数据的整理例1 晓军家里装修,准备安装节能灯.但听说:节能灯节电不省钱,还不如买普通白炽灯.到底买什么样的灯好?晓军决定亲自去市场调查一下.表28.2.5是他调查得到的数据.如果电费为0.60元/度,且用电度数计算公式为“用电度数=功率(瓦)×时间(时)
÷1 000”,你会建议晓军买哪种灯呢?(注:表中的功率是指达到相等亮度所需的功率)下面是晓军的分析:
计算各种灯使用5 000小时的花费情况,如表30.3.3所示.从上面的计算可以看出: 优质节能灯既节电又省钱.你觉得他的分析有道理吗?例2.某园林的门票每张10元(一次使用),考虑到人们的不同需求,也为了吸引更多的游客,该园林除了保留原来的售票方法外,还推出了一种“购买个人年票”的售票方法(个人年票从购票日起,可共持票者使用一年).年票分A、B、C三大类:A类年票每张120元,持票者进入园林时,无需再买门票;B类年票每张60元,持票者进入园林时,需再购门票,每次2元;C类年票每张40元,持票者进入园林时,需再购门票,每次3元.
(1)如果你只选择一种购买门票的方式,并且你计划在一年中用80元花在该园林的门票上,试通过计算,找出可使进入该园林的次数最多的购票方式;
(2)求一年中进入该园林至少超过多少次时,购买A类年票最合算.
分析:由题意可知,一共有四种购票方式.我们要作出决策,关键看一年所花门票费用与进入该园林的次数这两个量.
(1)只需对照每种购票方式,分别计算花80元能进入该园林的次数;
(2)显然,当进入该园林的次数较多时,选择购买A类年票较合算.那么“多”的标准究竟是多少呢?我们只需要分别计算出根据另三种方式花120元能进入该园林的最多次数即可.
解:(略)复习引入1.在一次中考模拟考试中,某校初三(1)班、初三(2)班两班学生数学成绩统计如下表:请你从平均数的角度判断,这两个班的考试成绩谁优谁次。
同学们,你们可曾接触过体育彩票?体育彩票的返奖率为55%.换句话说,平均每销售100元,将会有55元作为奖金奖励给购买体育彩票者中的幸运者(即中奖者),而另外的45元则用于支援国家或地方的体育事业的发展及销售体育彩票的成本费用.
对于55%的返奖率这一数据,能否理解为购买平均100张体育彩票就有55张中奖呢?从你接触到的人群中了解到的信息,中奖面有这么大吗?那么,到底平均要买几张才能得奖呢?理论数据与实际数据相符吗?如果返奖率确实为55%,而中奖面远远小于55%.请同学们讨论一下,究竟是什么原因造成的这一差异?
本节课,我们再来领略平均数在生活中的应用--2.平均要买几个才能得奖。例3.一家冷饮厂在电视里做广告,说他们厂生产的雪糕在小木棍上印有四种图案,集齐四个不同图案的小木棍就能够拼成一幅图,凭此可以在指定的商店领取一份礼物.假设该厂准备的四种图案的小木棍一样多,而且每支雪糕中夹入哪种图案的小木棍也完全是随机的,那么,平均要买几支雪糕才能得奖呢?
分 析:
如果幸运,也许买四支就能够得奖;但也有可能要买二十多支才得奖.那么平均要买几支才能得奖呢?不妨运用随机数,作模拟实验来解决这个难题.
令这四种图案的小木棍的编号分别为1号、2号、3号和4号.让计算器在1~4的范围每次产生一个随机整数,作为买到的那支雪糕小木棍的编号,记录下每次买到的编号以及每次得奖买了多少支雪糕.表28.3.2是小明10次实验的数据记录.平均要买几个才能获奖因为
所以小明认为大约平均买7支雪糕才能得奖.
思 考
你的实验记录与小明的记录相同吗?如果不相同,是否表明其中有一张记录是假的?你的实验结果与小明的相同吗?如果不相同,你有何建议?实践与探索例4.某啤酒厂推出一种有奖销售方案:该厂在出厂的所有啤酒的瓶盖内分别印上“再”、“来”、“一”、“瓶”、“啤”、“酒”六个字中的一个(文字颜色与啤酒颜色相近,从瓶外无法看清文字),集齐分别印有这六个不同文字的六个啤酒瓶盖就可换取一瓶该品牌的啤酒.假如印有这六个文字的瓶盖个数一样多,而且每瓶啤酒的瓶盖上印有哪个文字也完全是随机的,那么,平均要买多少瓶啤酒才能中奖(奖1瓶啤酒)呢?试通过模拟实验来解决这一问题.
分析:如果幸运的话,买6瓶啤酒也许就能中奖;但也许购买50瓶、100瓶都无法中奖.那么,平均要买多少瓶啤酒才能中奖呢?请你估计一个答案,写在纸上(最后与模拟实验得到的答案作个比较,看看你的估计能力如何).下面我们利用计算器进行模拟实验:让计算器在1~6的范围内每次产生一个随机整数,作为购买到的那瓶啤酒的瓶盖上的文字的代号(1代表“再”、2代表“来”、3代表“一”、4代表“瓶”、5代表“啤”、6代表“酒”),若“中奖”,则一次实验结束,然后进行下一次实验.记录下每次实验得到的相关数据,整理如下:因为,
所以我们可以估计大约平均要购买15瓶啤酒才能中奖.回顾:(1)此题如果要通过纯计算求出“平均要购买几瓶啤酒才能中奖”非常困难,同时我们也不太可能为了解出此题真的去购买啤酒,而利用计算器、通过模拟实验则相对“简单”地求出了答案.
(2)模拟实验前你估计的答案是什么?与现在求得的“大约15瓶”误差大不大?(3)本题的解法是通过实验去估计答案,因此要注意两点:①不同的人得到的答案不一定相同,即使同一个人再进行相同次数的实验答案也不一定相同;②要想答案尽可能准确,我们可以将实验次数尽可能地增加(但也要考虑到有无必要及可能性).因为实验次数充分大时,这个“平均数”将趋于稳定.例5.甲、乙、丙、丁四位小朋友一起做游戏:他们抛掷3枚硬币,若全部正面朝上,则甲胜;若全部反面朝上,则乙胜;若两枚正面朝上一枚反面朝上,则丙胜;若两枚反面朝上一枚正面朝上,则丁胜.将他们的获胜次数记录、统计如下表:当比赛进行到100次时,甲、乙两人连喊“运气不好”,至此游戏结束.
(1)分别计算游戏进行到30次、50次、100次时,甲、乙、丙、丁四位小朋友的获胜率;
(2)甲、乙两人真的是运气不好吗?请你运用所学知识帮助分析他们两人获胜率低的原因.分析:表面上看,抛掷3枚硬币,观察出现正面朝上的枚数共有四种情形,即这个游戏共有四个不同结果,好象比较“公平”. 但事实上,这四个结果是“等可能”的吗?
解:(1)游戏进行到30次、50次、100次时,甲、乙、丙、丁四位小朋友的获胜率如下表所示:(2)甲、乙两人并不真的是运气不好,而是因为这个游戏规则本身制订得并不公平.画出抛掷硬币的树状图(如图30.3.6):从树状图中可以看出:P(全部正面朝上)= P(全部反面朝上)= ;
而P(两枚正面朝上一枚反面朝上)= P(两枚反面朝上一枚正面朝上)= .
因此,按照原来的游戏规则,甲、乙获胜的概率只有丙、丁获胜的概率 的,故游戏不公平.探索: 针对上面的游戏,能否适当调整一下游戏规则,使得游戏对于四位小朋友来说做到公平?试给出两种不同的调整方案.
分析:调整方案关键在于将原规则中的不公平(获胜机会不均等)处去除,从而使得游戏公平.例如以下两种方案:
①实行积分制.甲获胜1次积3分,乙获胜1次积3分,丙获胜1次积1分,丁获胜1次积1分.这样到比赛结束看积分高低定胜负.
②甲与丙合作,乙与丁合作,即4位小朋友分成两个小组进行对抗比赛.按照原先的游戏规则比赛也能保证游戏公平. 回顾与反思 (1)游戏是否公平有时存在一定的隐蔽性,需要我们运用相关数学知识去分析、评判.而画树状图的关键则在于列出所有等可能出现的事件,从而确定各种结果出现的机会.
(2)有了以上的知识储备,现在,你对街头小巷的一些所谓的“公平游戏”会作如何评价?
课内练习与巩固
某商场春节期间进行有奖销售,规定每购买满50元商品可得刮刮卡一张,每张刮刮卡上印有“萬”、“事”、“如”、“意”四个字中的一个字,集齐分别印有“萬”、“事”、“如”、“意”四个字的四张刮刮卡即中奖——换取一张价值20元的购物券或领取一份价值20元的礼品包.假如印有“萬”、“事”、“如”、“意”的刮刮卡的张数一样多,而且每张刮刮卡上印有哪个字也完全是随机的,那么,平均要买满多少元商品才能中奖呢?试通过模拟实验来解决这一问题. 作业 课本P118 习题30.3第1-3题作业设计1.某校初三学生在一次数学测验中,甲、乙两班学生的成绩统计如下:请根据表格提供的信息回答下列问题:
(1)甲班学生成绩的众数为_________分,乙班学生成绩的众数为_________分.从众数看成绩较好的是__________班;
(2)甲班学生成绩的中位数为_________分,乙班学生成绩的中位数为_________分,甲班中成绩在中位数以上(包括中位数)的学生所占的百分比是_________%,乙班中成绩在中位数以上(包括中位数)的学生所占的百分比是_________%.从中位数看成绩较好的__________班;
(3)若成绩在85分以上的为优秀,则甲班的优秀率为_______%,
乙班的优秀率为______%,从优秀率看成绩较好的是__________班.
(4)请你根据题目给出的信息及以上的计算,对甲、乙两班的成绩作出你的综合评价.
2.某电视台综艺节目接到参与节目的热线电话及短信共3000个,现要从中抽取“幸运观众”10名,王蕾同学发了一条短信,那么她成为“幸运观众”的概率为__________.
3.将一副中国象棋的全部棋子装入一纸箱中,将纸箱封好后在其一个面上挖一方形孔,让此孔刚好能通过一枚棋子.小孔朝下,摇动纸箱,使从小孔中掉出一枚棋子.
(1)掉出的棋子是红“车”的概率是______________;
(2)掉出的棋子是“马”的概率是______________;
(3)掉出的棋子是“兵”或“卒”的概率是______________;
(4)掉出的棋子不是“车”、“马”、“炮”的概率是____________;
(5)请通过具体实验操作得出上述事件发生的可能性有多大,然后与你上面所填的概率结果作出比较,如果不相同,是不是“计算”与“实验”中一定有一项存在问题?4.有一种体育彩票,开奖号码为0000000~9999999之间的七位随机数(注:首位可以是0).若你购买到的号码恰好为开奖号码,则中特等奖;若你购买到的号码中连续6位与开奖号码对应相同(而且必须是相同数位,以下要求相同),则中一等奖;连续5位与开奖号码对应相同,则中二等奖;连续4位与开奖号码对应相同,则中三等奖;连续3位与开奖号码对应相同,则中四等奖;连续2位与开奖号码对应相同,则中五等奖.例如:若开奖号码为6579004,而你购买的号码为0079014,由于第3、4、5位号码相同,即连续3位与开奖号码对应相同,因此你中了四等奖.
(1)购买一张体育彩票中奖(等次不限)的机会大约有多大?
(2)试通过模拟实验求出平均要买多少张体育彩票才能中奖?谢谢
