2014-2015学年七年级数学下册(湘教版) 第五章第2节 旋转 课件(共16张PPT)
文档属性
| 名称 | 2014-2015学年七年级数学下册(湘教版) 第五章第2节 旋转 课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-11 06:37:00 | ||
图片预览





文档简介
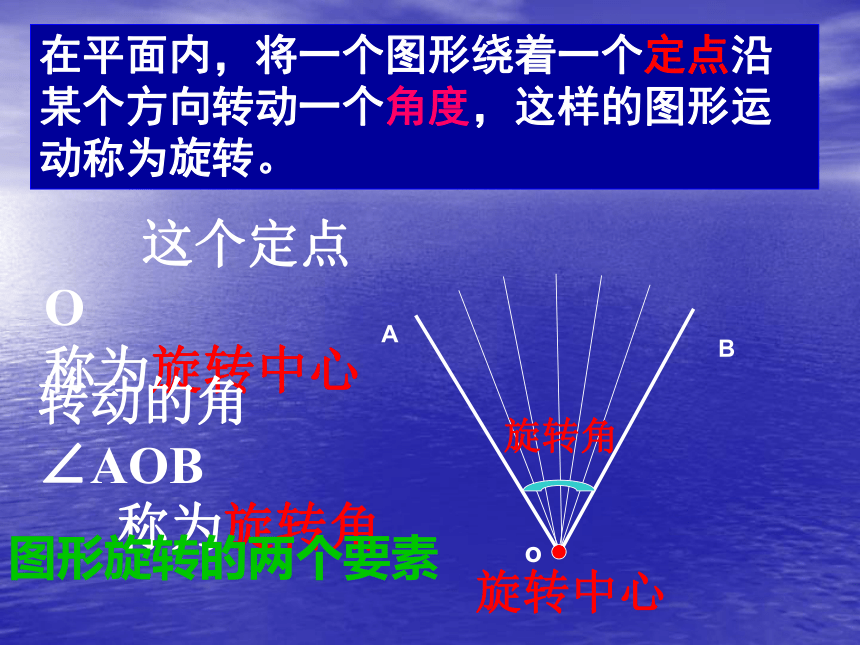
课件16张PPT。5.2 旋转 这种转动现象,有什么共同的特征?形状和大小改变吗?在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转旋转不改变图形的大小和形状。 这个定点O
称为旋转中心旋转角旋转中心在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。AoB转动的角∠AOB
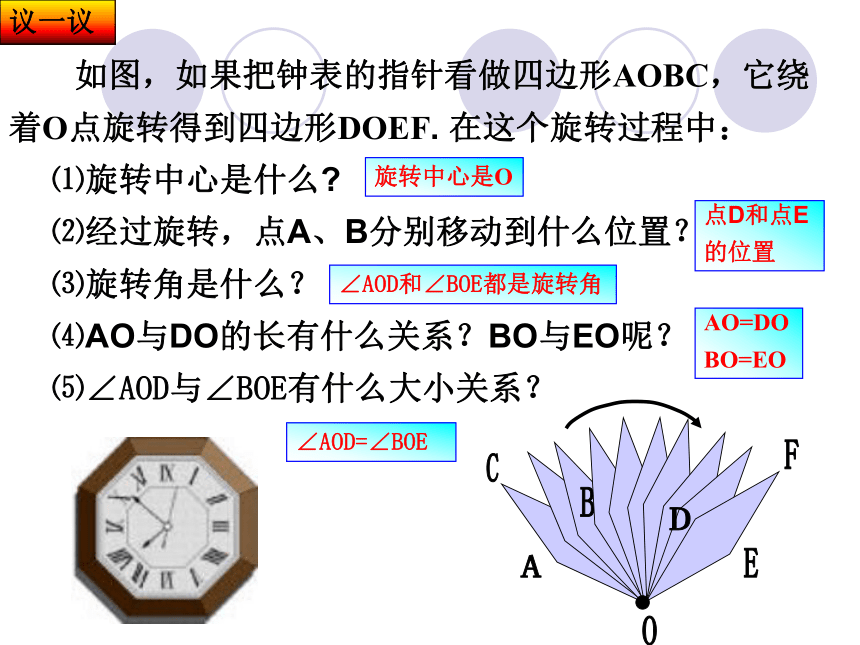
称为旋转角图形旋转的两个要素 如图,如果把钟表的指针看做四边形AOBC,它绕
着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是什么?
⑵经过旋转,点A、B分别移动到什么位置?
⑶旋转角是什么?
⑷AO与DO的长有什么关系?BO与EO呢?
⑸∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点E
的位置AO=DO
BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEFOP′P 钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?例题1.旋转的画法1: 画△ABC绕顶点A顺时针旋转45°的图形.ABCB′C′画法:45°⑴以A为顶点, AB为边顺时针方向作∠BAB =45°,′并截取AB =AB;′⑵同样画边AC , 并连结BC ;′′′则△ABC 就是所求作的旋转图形.′′45°你能说说旋转中有哪些对应元素吗?例题2.画?ABC绕点O逆时针旋转90°.例题2.旋转的画法2:0ABC·A′B′C′90°画法:⑴连结OA、OB、OC;⑵分别画OA、OB、OC绕点O逆时针旋转90°的线段OA、OB、OC ;′′′⑶顺次连结AB、BC、CA .′′′′′′旋转的画法3:例题2.O·把下列格点图形顺时针旋转90°AA′B′ 这样旋转几次可以
与原来的图形重合? 如图:?ABC是等边三角形,D是BC
上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?解:(1)旋转中心是顶点A;(2)旋转了60度;(3)点M转到了AC的中点位置上.例题3.·旋转角∠BAC 如图等腰直角?ABC逆时针旋转到
?ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少?
⑵DE与AC的位置关系有什么特征?解:⑴旋转中心是顶点A,旋转角度是∠BAD=45°;⑵ DE⊥AC.例题4.ABCDE┌O因为∠CAE=45°, 且∠E=45°.2.如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O例题5.解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.ABCPQRO探索如图△ABC是等边三角形,△ ACQ和△BCR都是可以由△ABP旋转得到的,⑴分别说明旋转中心和旋转角度; ⑵△BCR可以由△ACQ旋转得到吗?课堂小结⑴旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动⑵旋转的要素:旋转不改变图形大小和形状,只改变图形的位置.叫做图形的旋转,简称旋转.旋转中心和旋转角.⑶旋转的特征:再 见
称为旋转中心旋转角旋转中心在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。AoB转动的角∠AOB
称为旋转角图形旋转的两个要素 如图,如果把钟表的指针看做四边形AOBC,它绕
着O点旋转得到四边形DOEF. 在这个旋转过程中:
⑴旋转中心是什么?
⑵经过旋转,点A、B分别移动到什么位置?
⑶旋转角是什么?
⑷AO与DO的长有什么关系?BO与EO呢?
⑸∠AOD与∠BOE有什么大小关系?议一议旋转中心是O点D和点E
的位置AO=DO
BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEFOP′P 钟表的分针匀速旋转一周需要60分.
(1)指出它的旋转中心;
(2)经过20分,分针旋转了多少度?例题1.旋转的画法1: 画△ABC绕顶点A顺时针旋转45°的图形.ABCB′C′画法:45°⑴以A为顶点, AB为边顺时针方向作∠BAB =45°,′并截取AB =AB;′⑵同样画边AC , 并连结BC ;′′′则△ABC 就是所求作的旋转图形.′′45°你能说说旋转中有哪些对应元素吗?例题2.画?ABC绕点O逆时针旋转90°.例题2.旋转的画法2:0ABC·A′B′C′90°画法:⑴连结OA、OB、OC;⑵分别画OA、OB、OC绕点O逆时针旋转90°的线段OA、OB、OC ;′′′⑶顺次连结AB、BC、CA .′′′′′′旋转的画法3:例题2.O·把下列格点图形顺时针旋转90°AA′B′ 这样旋转几次可以
与原来的图形重合? 如图:?ABC是等边三角形,D是BC
上一点, ?ABD经过 旋转后到达?ACE的位置。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB的中点,那么经过上述旋
转后,点M转到了什么位置?解:(1)旋转中心是顶点A;(2)旋转了60度;(3)点M转到了AC的中点位置上.例题3.·旋转角∠BAC 如图等腰直角?ABC逆时针旋转到
?ADE, 使AD⊥BC, 垂足为O, 试说明:。
⑴旋转中心是哪一点?旋转角度是多少?
⑵DE与AC的位置关系有什么特征?解:⑴旋转中心是顶点A,旋转角度是∠BAD=45°;⑵ DE⊥AC.例题4.ABCDE┌O因为∠CAE=45°, 且∠E=45°.2.如图,正方形ABCD和正方形CDEF有公共边CD,请设计方案,使正方形ABCD旋转后能与正方形CDEF重合,你能写出几种方案?ABCDEF·O例题5.解:方案一:把正方形ABCD绕点D顺时针旋转90°.方案二:把正方形ABCD绕点C逆时针旋转90°.方案三:把正方形ABCD绕CD的中点O旋转180°.ABCPQRO探索如图△ABC是等边三角形,△ ACQ和△BCR都是可以由△ABP旋转得到的,⑴分别说明旋转中心和旋转角度; ⑵△BCR可以由△ACQ旋转得到吗?课堂小结⑴旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动⑵旋转的要素:旋转不改变图形大小和形状,只改变图形的位置.叫做图形的旋转,简称旋转.旋转中心和旋转角.⑶旋转的特征:再 见
