北师大版数学八年级上册 7.3平行线的判定教学设计
文档属性
| 名称 | 北师大版数学八年级上册 7.3平行线的判定教学设计 |  | |
| 格式 | doc | ||
| 文件大小 | 703.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 16:14:11 | ||
图片预览

文档简介
《7.3 平行线的判定》教案
1、教学目标
(1)知识与技能:会根据“同位角相等,两直线平行”这一基本事实证明“内错角相等,两直线平行”、“同旁内角互补,两直线平行”;能运用平行线的判定解决简单问题;初步了解证明的基本步骤和书写格式。
(2)过程与方法:经历探究证明定理的思路和证题过程,合作交流,进一步理解证明的步骤、格式和方法。体会由特殊到一般、转化、一题多解等数学思想方法。
(3)情感态度价值观:在探索的过程中学会与他人合作,并体会在解决问题的过程中与他人合作的重要性。
2、重点难点
重点:判定定理的证明及其应用。
难点:定理证明的思路分析以及书写方法。
3、教学过程
教学活动 学生活动 教师活动 设计意图
【第一环节】回顾平行线的判定条件1.两条直线平行的判定条件有:(1)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”(2)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”(3)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”2.在这三个条件中,哪一个是上一节课已经确认了的公理? 学生回顾思考平行线的定义及两直线平行的三种判定方法. 教师应重点关注:(1)学生参与思考问题的积极性;(2)学生能否准确、全面地地回答出直线平行的判定方法。(3)板书“公理:同位角相等,两直线平行”。 采用复习引入的方式,以问题唤醒学生的回忆,引起学生对两直线平行的判定的思考。
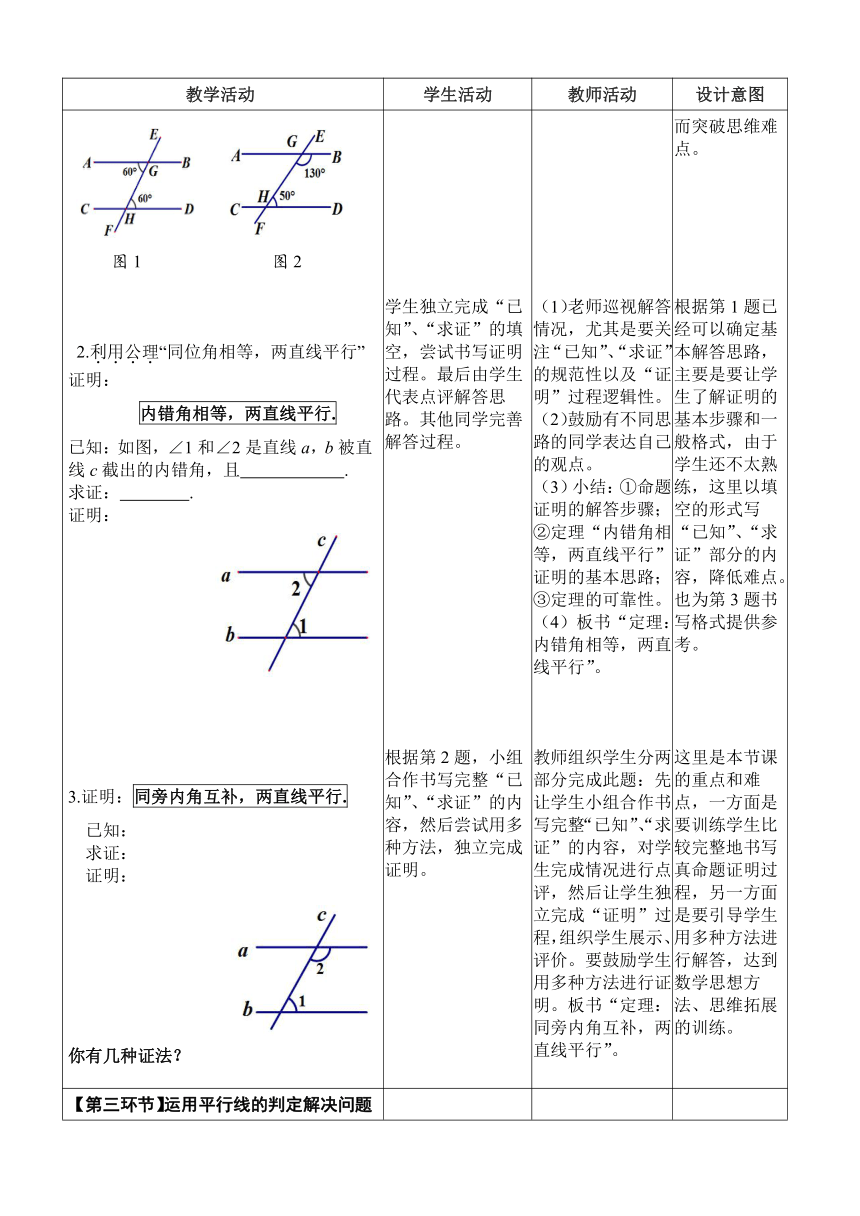
【第二环节】证明平行线的判定定理利用公理“同位角相等,两直线平行”说明下列图1、图2中的AB与CD是否平行. 图1 图2 2.利用公理“同位角相等,两直线平行”证明:内错角相等,两直线平行.已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且 .求证: .证明:3.证明:同旁内角互补,两直线平行. 已知: 求证: 证明:你有几种证法? 学生独立思考后,口头回答第1个问题。学生独立完成“已知”、“求证”的填空,尝试书写证明过程。最后由学生代表点评解答思路。其他同学完善解答过程。根据第2题,小组合作书写完整“已知”、“求证”的内容,然后尝试用多种方法,独立完成证明。 教师引导、小结把内错角、同旁内角转化为同位角进行解决问题。(1)老师巡视解答情况,尤其是要关注“已知”、“求证”的规范性以及“证明”过程逻辑性。(2)鼓励有不同思路的同学表达自己的观点。(3)小结:①命题证明的解答步骤;②定理“内错角相等,两直线平行”证明的基本思路;③定理的可靠性。(4)板书“定理:内错角相等,两直线平行”。教师组织学生分两部分完成此题:先让学生小组合作书写完整“已知”、“求证”的内容,对学生完成情况进行点评,然后让学生独立完成“证明”过程,组织学生展示、评价。要鼓励学生用多种方法进行证明。板书“定理:同旁内角互补,两直线平行”。 让学生解决特殊实例,由特殊到一般,将内错角、同旁内角转化为同位角进行解决问题为证明定理做铺垫,从而突破思维难点。根据第1题已经可以确定基本解答思路,主要是要让学生了解证明的基本步骤和一般格式,由于学生还不太熟练,这里以填空的形式写“已知”、“求证”部分的内容,降低难点。也为第3题书写格式提供参考。这里是本节课的重点和难点,一方面是要训练学生比较完整地书写真命题证明过程,另一方面是要引导学生用多种方法进行解答,达到数学思想方法、思维拓展的训练。
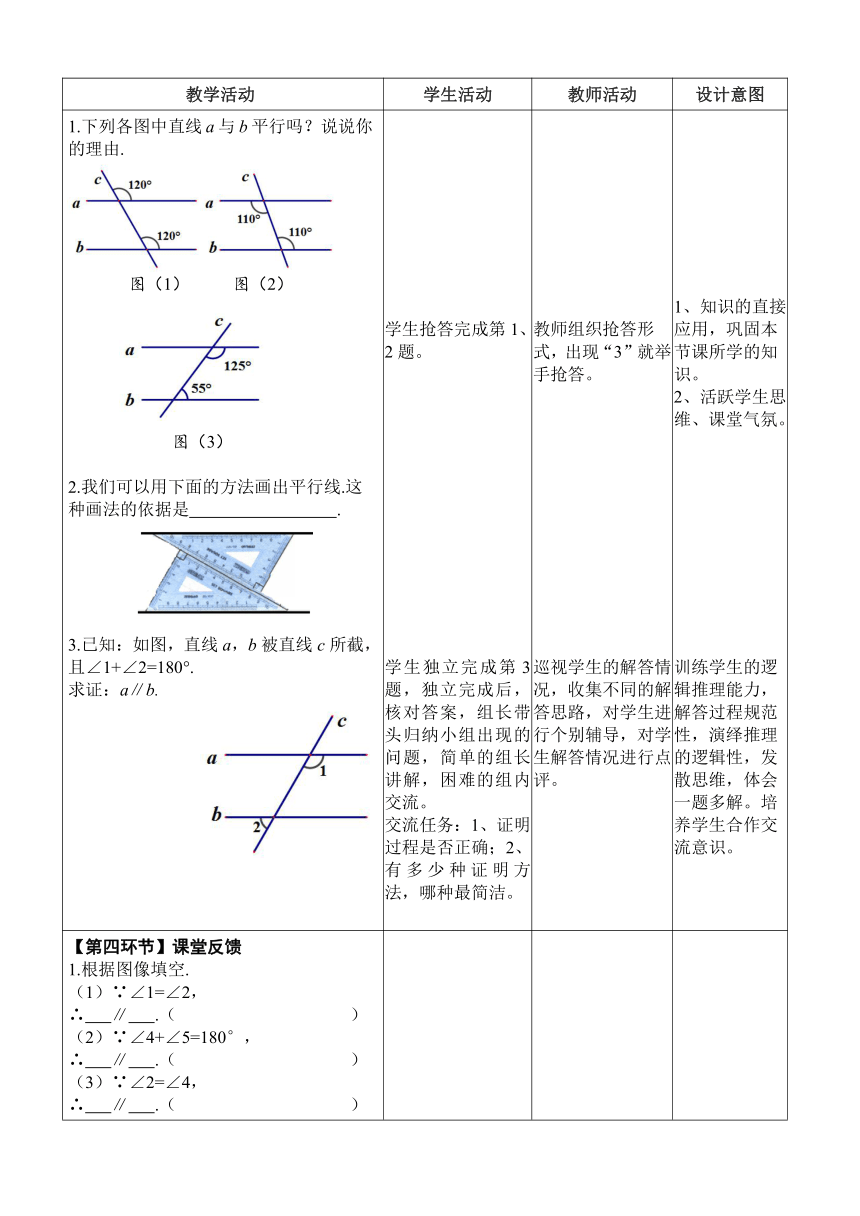
【第三环节】运用平行线的判定解决问题1.下列各图中直线a与b平行吗?说说你的理由. 图(1) 图(2) 图(3)2.我们可以用下面的方法画出平行线.这种画法的依据是 .3.已知:如图,直线a,b被直线c所截,且∠1+∠2=180°.求证:a∥b. 学生抢答完成第1、2题。学生独立完成第3题,独立完成后,核对答案,组长带头归纳小组出现的问题,简单的组长讲解,困难的组内交流。交流任务:1、证明过程是否正确;2、有多少种证明方法,哪种最简洁。 教师组织抢答形式,出现“3”就举手抢答。巡视学生的解答情况,收集不同的解答思路,对学生进行个别辅导,对学生解答情况进行点评。 1、知识的直接应用,巩固本节课所学的知识。2、活跃学生思维、课堂气氛。训练学生的逻辑推理能力,解答过程规范性,演绎推理的逻辑性,发散思维,体会一题多解。培养学生合作交流意识。
【第四环节】课堂反馈1.根据图像填空.(1)∵∠1=∠2,∴ ∥ .( )∵∠4+∠5=180°,∴ ∥ .( )∵∠2=∠4,∴ ∥ .( )∵∠1+∠5=180°,∴ ∥ .( )2.如图,一个零件ABCD需要AB边与CD边平行,现测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?请说明理由. 学生独立完成本环节,然后核对答案。 巡视学生的活动,关注学生能否准确书写过程。展示答案,了解学生的解答情况,对于学生做错比较多的及时采取补救措施。 第1题是课本习题的改编题,这种改编方式有利于学生独立完成,并检测学生的学习情况;第2题是实际应用题,树立“数学源于生活,用于生活”的意识。
【第五环节】总结反思通过本节课的学习,你有什么收获?和其他同学分享你的收获:(1)知识方面(2)方法方面(3)其他方面 学生畅所欲言,交流自己的收获与疑 惑。 (1)在此活动中,教师应重点关注:学生三维目标的达成度,适时进行引导和总结。(2)完善并板书判定的几何语言表达。 设置半开放性问题,设置三个方面,这样设计,一方面考虑学生的总结能力、表达能力还比较欠缺,另一方面有利于了解学生三维目标的达成度。
3、课后作业
Ⅰ必做题:
1.蜂房的顶部由三个全等的四边形围成.每个四边形的形状如图所示,其中
∠α=109°28′,∠β=70°32′.试确定这个四边形对边的位置关系,并证明你的结论.(提示:1°=60′)
2.已知:如图,点D,E分别在AB和AC上,CD平分∠ACB,∠DCB=40°,∠AED=80°.求证:DE∥BC.
3.已知:如图,直线a,b被直线c所截,且∠1+∠2=180°.
求证:a∥b.
Ⅱ选做题:
4.如图,∠B=70°,∠BDC=110°,∠E=70°,图中有几组平行线?请说明理由.
5.实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图所示是光线从空气射入玻璃中,再从玻璃射入空气中的示意图.已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?请说明理由.
【设计意图】必做题部分是课本的题目,比较基础,为本节课所学的知识起到巩固的作用,全体同学都应该掌握的;选做部分的题目是为学有余力的同学做思维提高训练。其中,第4题是纯数学知识的综合应用,第5题是跨学科的综合应用。这样设计也可以增加课堂的伸缩性,如果课堂时间比较充裕,就可以利用一些时间来分析和解答选做题。
4、设计反思
1、本节课的设计,注重学生的最近发展区,例如:第一环节的第1题,用特殊的例子来引导学生进行思路的分析。
2、选题具有层次性,本节课例题、练习都是层层递进,由“内错角相等,两直线平行”到“同旁内角互补,两直线平行”书写格式的铺垫,再由必做题的基础性题目到选做题的综合性题目,无处不体现选题的层次性。
3、本节课的设计基于课本又不唯“本”,设计环节、知识体系基本是以课本为主,但是又有所创新,例如:第一环节的第1题特殊例子的引入。再如:第四环节第1题是课本的改编题,这样的改编更利于课堂反馈。
当然,本节课可能还有更合理的设计,作为新秀的我会不断努力学习别人优秀的经验!
1、教学目标
(1)知识与技能:会根据“同位角相等,两直线平行”这一基本事实证明“内错角相等,两直线平行”、“同旁内角互补,两直线平行”;能运用平行线的判定解决简单问题;初步了解证明的基本步骤和书写格式。
(2)过程与方法:经历探究证明定理的思路和证题过程,合作交流,进一步理解证明的步骤、格式和方法。体会由特殊到一般、转化、一题多解等数学思想方法。
(3)情感态度价值观:在探索的过程中学会与他人合作,并体会在解决问题的过程中与他人合作的重要性。
2、重点难点
重点:判定定理的证明及其应用。
难点:定理证明的思路分析以及书写方法。
3、教学过程
教学活动 学生活动 教师活动 设计意图
【第一环节】回顾平行线的判定条件1.两条直线平行的判定条件有:(1)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”(2)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”(3)两条直线被第三条直线所截,如果 ,那么这两条直线平行.简称“ ,两直线平行.”2.在这三个条件中,哪一个是上一节课已经确认了的公理? 学生回顾思考平行线的定义及两直线平行的三种判定方法. 教师应重点关注:(1)学生参与思考问题的积极性;(2)学生能否准确、全面地地回答出直线平行的判定方法。(3)板书“公理:同位角相等,两直线平行”。 采用复习引入的方式,以问题唤醒学生的回忆,引起学生对两直线平行的判定的思考。
【第二环节】证明平行线的判定定理利用公理“同位角相等,两直线平行”说明下列图1、图2中的AB与CD是否平行. 图1 图2 2.利用公理“同位角相等,两直线平行”证明:内错角相等,两直线平行.已知:如图,∠1和∠2是直线a,b被直线c截出的内错角,且 .求证: .证明:3.证明:同旁内角互补,两直线平行. 已知: 求证: 证明:你有几种证法? 学生独立思考后,口头回答第1个问题。学生独立完成“已知”、“求证”的填空,尝试书写证明过程。最后由学生代表点评解答思路。其他同学完善解答过程。根据第2题,小组合作书写完整“已知”、“求证”的内容,然后尝试用多种方法,独立完成证明。 教师引导、小结把内错角、同旁内角转化为同位角进行解决问题。(1)老师巡视解答情况,尤其是要关注“已知”、“求证”的规范性以及“证明”过程逻辑性。(2)鼓励有不同思路的同学表达自己的观点。(3)小结:①命题证明的解答步骤;②定理“内错角相等,两直线平行”证明的基本思路;③定理的可靠性。(4)板书“定理:内错角相等,两直线平行”。教师组织学生分两部分完成此题:先让学生小组合作书写完整“已知”、“求证”的内容,对学生完成情况进行点评,然后让学生独立完成“证明”过程,组织学生展示、评价。要鼓励学生用多种方法进行证明。板书“定理:同旁内角互补,两直线平行”。 让学生解决特殊实例,由特殊到一般,将内错角、同旁内角转化为同位角进行解决问题为证明定理做铺垫,从而突破思维难点。根据第1题已经可以确定基本解答思路,主要是要让学生了解证明的基本步骤和一般格式,由于学生还不太熟练,这里以填空的形式写“已知”、“求证”部分的内容,降低难点。也为第3题书写格式提供参考。这里是本节课的重点和难点,一方面是要训练学生比较完整地书写真命题证明过程,另一方面是要引导学生用多种方法进行解答,达到数学思想方法、思维拓展的训练。
【第三环节】运用平行线的判定解决问题1.下列各图中直线a与b平行吗?说说你的理由. 图(1) 图(2) 图(3)2.我们可以用下面的方法画出平行线.这种画法的依据是 .3.已知:如图,直线a,b被直线c所截,且∠1+∠2=180°.求证:a∥b. 学生抢答完成第1、2题。学生独立完成第3题,独立完成后,核对答案,组长带头归纳小组出现的问题,简单的组长讲解,困难的组内交流。交流任务:1、证明过程是否正确;2、有多少种证明方法,哪种最简洁。 教师组织抢答形式,出现“3”就举手抢答。巡视学生的解答情况,收集不同的解答思路,对学生进行个别辅导,对学生解答情况进行点评。 1、知识的直接应用,巩固本节课所学的知识。2、活跃学生思维、课堂气氛。训练学生的逻辑推理能力,解答过程规范性,演绎推理的逻辑性,发散思维,体会一题多解。培养学生合作交流意识。
【第四环节】课堂反馈1.根据图像填空.(1)∵∠1=∠2,∴ ∥ .( )∵∠4+∠5=180°,∴ ∥ .( )∵∠2=∠4,∴ ∥ .( )∵∠1+∠5=180°,∴ ∥ .( )2.如图,一个零件ABCD需要AB边与CD边平行,现测得拐角∠ABC=120°,∠BCD=60°,这个零件合格吗?请说明理由. 学生独立完成本环节,然后核对答案。 巡视学生的活动,关注学生能否准确书写过程。展示答案,了解学生的解答情况,对于学生做错比较多的及时采取补救措施。 第1题是课本习题的改编题,这种改编方式有利于学生独立完成,并检测学生的学习情况;第2题是实际应用题,树立“数学源于生活,用于生活”的意识。
【第五环节】总结反思通过本节课的学习,你有什么收获?和其他同学分享你的收获:(1)知识方面(2)方法方面(3)其他方面 学生畅所欲言,交流自己的收获与疑 惑。 (1)在此活动中,教师应重点关注:学生三维目标的达成度,适时进行引导和总结。(2)完善并板书判定的几何语言表达。 设置半开放性问题,设置三个方面,这样设计,一方面考虑学生的总结能力、表达能力还比较欠缺,另一方面有利于了解学生三维目标的达成度。
3、课后作业
Ⅰ必做题:
1.蜂房的顶部由三个全等的四边形围成.每个四边形的形状如图所示,其中
∠α=109°28′,∠β=70°32′.试确定这个四边形对边的位置关系,并证明你的结论.(提示:1°=60′)
2.已知:如图,点D,E分别在AB和AC上,CD平分∠ACB,∠DCB=40°,∠AED=80°.求证:DE∥BC.
3.已知:如图,直线a,b被直线c所截,且∠1+∠2=180°.
求证:a∥b.
Ⅱ选做题:
4.如图,∠B=70°,∠BDC=110°,∠E=70°,图中有几组平行线?请说明理由.
5.实验发现:光线从空气射入玻璃中,会发生折射现象,光线从玻璃射入空气中,同样也会发生折射现象.如图所示是光线从空气射入玻璃中,再从玻璃射入空气中的示意图.已知∠1=∠2,∠3=∠4,那么光线AB与CD是否平行?请说明理由.
【设计意图】必做题部分是课本的题目,比较基础,为本节课所学的知识起到巩固的作用,全体同学都应该掌握的;选做部分的题目是为学有余力的同学做思维提高训练。其中,第4题是纯数学知识的综合应用,第5题是跨学科的综合应用。这样设计也可以增加课堂的伸缩性,如果课堂时间比较充裕,就可以利用一些时间来分析和解答选做题。
4、设计反思
1、本节课的设计,注重学生的最近发展区,例如:第一环节的第1题,用特殊的例子来引导学生进行思路的分析。
2、选题具有层次性,本节课例题、练习都是层层递进,由“内错角相等,两直线平行”到“同旁内角互补,两直线平行”书写格式的铺垫,再由必做题的基础性题目到选做题的综合性题目,无处不体现选题的层次性。
3、本节课的设计基于课本又不唯“本”,设计环节、知识体系基本是以课本为主,但是又有所创新,例如:第一环节的第1题特殊例子的引入。再如:第四环节第1题是课本的改编题,这样的改编更利于课堂反馈。
当然,本节课可能还有更合理的设计,作为新秀的我会不断努力学习别人优秀的经验!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
