4.1等式与方程课件
图片预览






文档简介
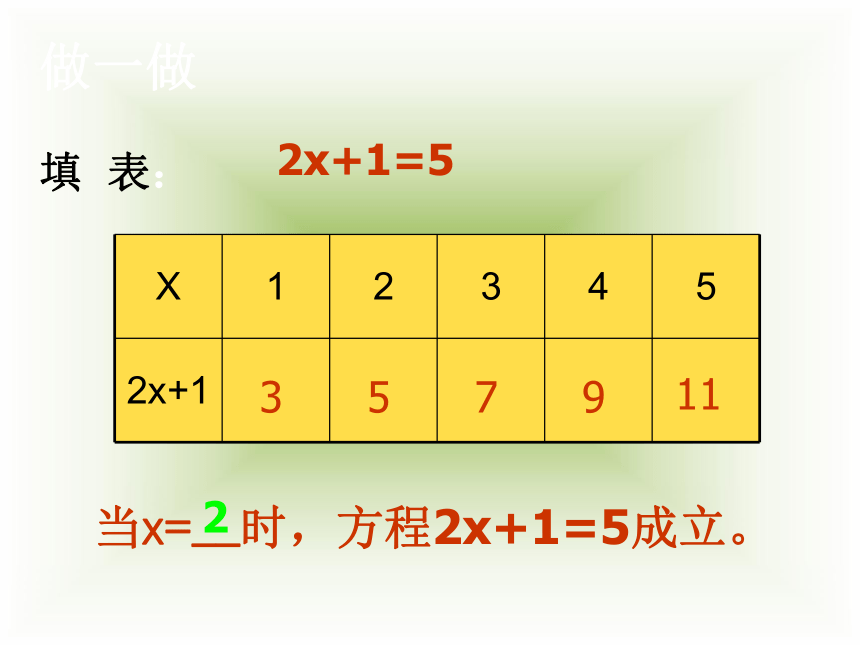
课件31张PPT。 等式与方程方程含有未知数的等式.只含有一个未知数(元)x, 未知数x的次数都是1次的方程.一元一次方程 像这样用等号“=”来表示相等关系的式子叫作等式.左边右边??2x+1=53m+2=1-m下列方程是一元一次方程吗?如何求其中的未知数的值呢?做一做填 表:357911当x=__时,方程2x+1=5成立。22x+1=5 分别把0、1、2、3、4
代入下列方程,哪一个能使方程成立: 2x-1=5x=0时,方程的左边=___,右边=___.x=4时,方程的左边=___,右边=___.x=2时,方程的左边=___,右边=___.x=3时,方程的左边=___,右边=___.-15x=1时,方程的左边=___,右边=___.55551357所以x=3时,能使方程成立.x=3是方程2x-1=5的解. 使方程左右两边相等的未知数的值叫做方程的解
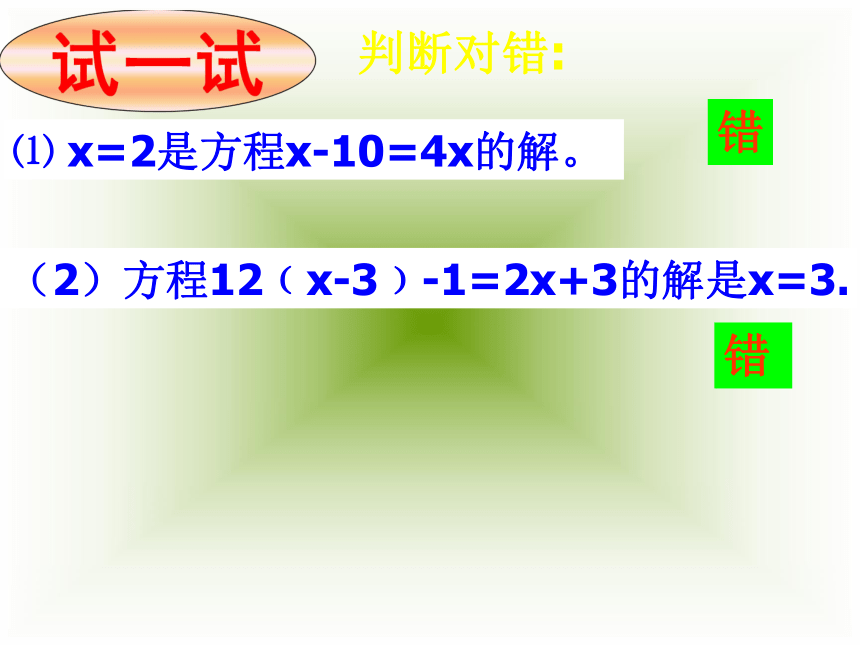
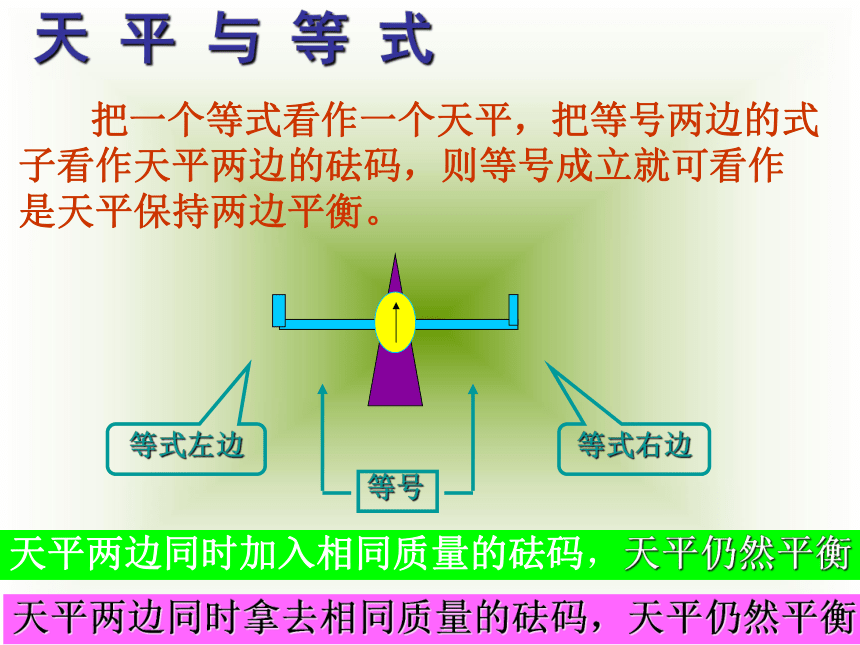
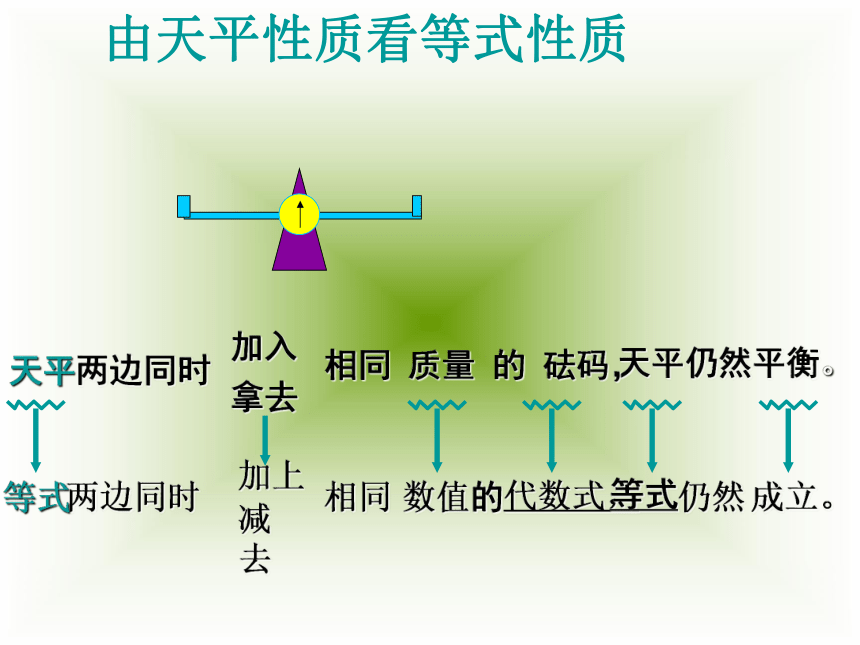
求方程的解的过程叫做解方程方程的解和解方程的概念⑴ x=2是方程x-10=4x的解。 (2)方程12﹙x-3﹚-1=2x+3的解是x=3.判断对错:错错天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天平两边同时加入相同质量的砝码,天平仍然平衡天平两边同时拿去相同质量的砝码,天平仍然平衡由天平性质看等式性质天平两边同时天平仍然平衡。加入拿去相同 质量 的 砝码,等式加上减去数值代数式,等式成立。+—等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.如果a=b,那么a±c=b±c 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还能保持平衡吗?
于是 , 你又能得出等式的什么性质? 等式的性质2:等式两边乘同一个数或除以同一个不为0的数,结果仍相等.×3÷3??如果a=b,那么ac=bc如果a=b(c≠0),那么等 式 的 性 质 【等式性质2】【等式性质1】口答练习:(1) 从 x = y 能不能得到 x +5 = y + 5 , 为什么?(2) 从 x = y 能不能得到 , 为什么?(3) 从 a+2=b+2 能不能得到 a=b , 为什么?(4) 从-3a=-3b 能不能得到 a=b , 为什么?(5) 从 3ac=4a 能不能得到 3c=4 , 为什么?1.下列说法错误的是( ).C(因为x可能等于0)(等量代换)(对称性)方程2x+1=5的变形过程:2x+1=5两边都减去12x=4两边都除以2 x=2两边各取走1个两边个数都除以2数学实验室你能说出方程 3x=2x+3 是怎么变形的吗?两边都减去2xx=33x=2x+3数学实验室填空:
解方程:-5y=-3y+2
解:两边同时加3y,得
-5y+3y=-3y+2+_____
合并同类项得:-2y=2
两边同时除以-2, 得Y=____
3y-1⑴ x+5=2解:⑴x+5-5=2-5合并同类项,得x=-3利用等式性质 , 解下列方程: 把求出的解代入原方程,可以检验解方程是否正确两边都减去5,得例1⑵ -2x=4⑵两边都除以-2,得
=即x=-2解:利用等式性质 , 解下列方程: 把求出的解代入原方程,可以检验解方程是否正确例1解下列方程:(1) x+2=-6(2) -6x=2练一练⑴ 3x-2=x例2、利用等式性质 , 解下列方程: 解:两边同时减x, 得 3x-2-x=x-x
合并同类项,得 2x-2=0
两边同时加2,得 2x-2+2=0+2
合并同类项 ,得 2x=2
两边同时除以2,得 x=1
例2、利用等式性质 , 解下列方程: (2)7x+2=-3x+3解:两边同时加3x,得
7x+2+3x=-3x+3+3x
合并同类项,得 10x+2=3
两边同时减2,得 10x+2-2=3-2
合并同类项 ,得 10x=1
两边同时除以10,得 x=0.1
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.1、解下列方程:(1) -3x=3-4x(2) -6x+2=-3x-1练一练D D4、在学习了等式的性质后,Mahou发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是他随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此, Mahou 顿时就傻了:居然得出如此等式!于是 Mahou 开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让 Mahou 的愁眉在恍然大悟中舒展开来吗?
代入下列方程,哪一个能使方程成立: 2x-1=5x=0时,方程的左边=___,右边=___.x=4时,方程的左边=___,右边=___.x=2时,方程的左边=___,右边=___.x=3时,方程的左边=___,右边=___.-15x=1时,方程的左边=___,右边=___.55551357所以x=3时,能使方程成立.x=3是方程2x-1=5的解. 使方程左右两边相等的未知数的值叫做方程的解
求方程的解的过程叫做解方程方程的解和解方程的概念⑴ x=2是方程x-10=4x的解。 (2)方程12﹙x-3﹚-1=2x+3的解是x=3.判断对错:错错天 平 与 等 式 把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平保持两边平衡。天平两边同时加入相同质量的砝码,天平仍然平衡天平两边同时拿去相同质量的砝码,天平仍然平衡由天平性质看等式性质天平两边同时天平仍然平衡。加入拿去相同 质量 的 砝码,等式加上减去数值代数式,等式成立。+—等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等.如果a=b,那么a±c=b±c 如果天平两边砝码的质量同时扩大相同的倍数(或同时缩小为原来的几分之一),那么天平还能保持平衡吗?
于是 , 你又能得出等式的什么性质? 等式的性质2:等式两边乘同一个数或除以同一个不为0的数,结果仍相等.×3÷3??如果a=b,那么ac=bc如果a=b(c≠0),那么等 式 的 性 质 【等式性质2】【等式性质1】口答练习:(1) 从 x = y 能不能得到 x +5 = y + 5 , 为什么?(2) 从 x = y 能不能得到 , 为什么?(3) 从 a+2=b+2 能不能得到 a=b , 为什么?(4) 从-3a=-3b 能不能得到 a=b , 为什么?(5) 从 3ac=4a 能不能得到 3c=4 , 为什么?1.下列说法错误的是( ).C(因为x可能等于0)(等量代换)(对称性)方程2x+1=5的变形过程:2x+1=5两边都减去12x=4两边都除以2 x=2两边各取走1个两边个数都除以2数学实验室你能说出方程 3x=2x+3 是怎么变形的吗?两边都减去2xx=33x=2x+3数学实验室填空:
解方程:-5y=-3y+2
解:两边同时加3y,得
-5y+3y=-3y+2+_____
合并同类项得:-2y=2
两边同时除以-2, 得Y=____
3y-1⑴ x+5=2解:⑴x+5-5=2-5合并同类项,得x=-3利用等式性质 , 解下列方程: 把求出的解代入原方程,可以检验解方程是否正确两边都减去5,得例1⑵ -2x=4⑵两边都除以-2,得
=即x=-2解:利用等式性质 , 解下列方程: 把求出的解代入原方程,可以检验解方程是否正确例1解下列方程:(1) x+2=-6(2) -6x=2练一练⑴ 3x-2=x例2、利用等式性质 , 解下列方程: 解:两边同时减x, 得 3x-2-x=x-x
合并同类项,得 2x-2=0
两边同时加2,得 2x-2+2=0+2
合并同类项 ,得 2x=2
两边同时除以2,得 x=1
例2、利用等式性质 , 解下列方程: (2)7x+2=-3x+3解:两边同时加3x,得
7x+2+3x=-3x+3+3x
合并同类项,得 10x+2=3
两边同时减2,得 10x+2-2=3-2
合并同类项 ,得 10x=1
两边同时除以10,得 x=0.1
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的等式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.1、解下列方程:(1) -3x=3-4x(2) -6x+2=-3x-1练一练D D4、在学习了等式的性质后,Mahou发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是他随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此, Mahou 顿时就傻了:居然得出如此等式!于是 Mahou 开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让 Mahou 的愁眉在恍然大悟中舒展开来吗?
