人教A版高中数学 选择性必修一 《3.1.2椭圆的简单几何性质(1)》 教案(含教学反思)
文档属性
| 名称 | 人教A版高中数学 选择性必修一 《3.1.2椭圆的简单几何性质(1)》 教案(含教学反思) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 20:03:42 | ||
图片预览




文档简介
人教A版高中数学选择性必修一
《3.1.2椭圆的简单几何性质(1)》教学设计
【教材分析】
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习椭圆的简单几何性质,教材的地位和作用地位:本节课是在椭圆的概念和标准方程的基础上,运用代数的方法,研究椭圆的简单几何性质及简单应用 . 本节课内容的掌握程度直接影响学习双曲线和抛物线几何性质.作用:提高学生的数学素质,培养学生的数形结合思想,及分析问题和解决问题的能力.因此,内容在解析几何中占有非常重要的地位.
【学情分析】
椭圆是高中数学课程内容中较难的一章节,需要学生具备良好的解析几何思维以及综合计算能力,通过学习椭圆,理解其几何意义,掌握其标准方程和几何性质,并会综合应用解决问题,在本节课程学习中,要注重学生对概念的理解,从简单的题目入手,直接应用性质解题,循序渐进,逐步掌握综合应用题目的解题思路和方法.
【教学目标与核心素养】
教学目标:
A. 掌握椭圆的几何性质,掌握a,b,c,e的几何意义及a,b,c,e之间的相互关系.
B.尝试利用椭圆的方程研究椭圆的几何性质.
C.尝试利用椭圆的知识解决简单的实际问题.
核心素养:
1.数学抽象:椭圆的几何性质
2.逻辑推理:利用椭圆的方程研究椭圆的几何性
3.数学运算:利用椭圆的方程研究椭圆的几何性
4.数学建模:利用椭圆的知识解决应用问题
5.直观想象:离心率的几何意义
【教学重点】
由几何条件求出椭圆的方程
【教学难点】
由椭圆的方程研究椭圆的几何性质
【教学方法】
启发教学法,讲授法
【教学过程】
情境导入:
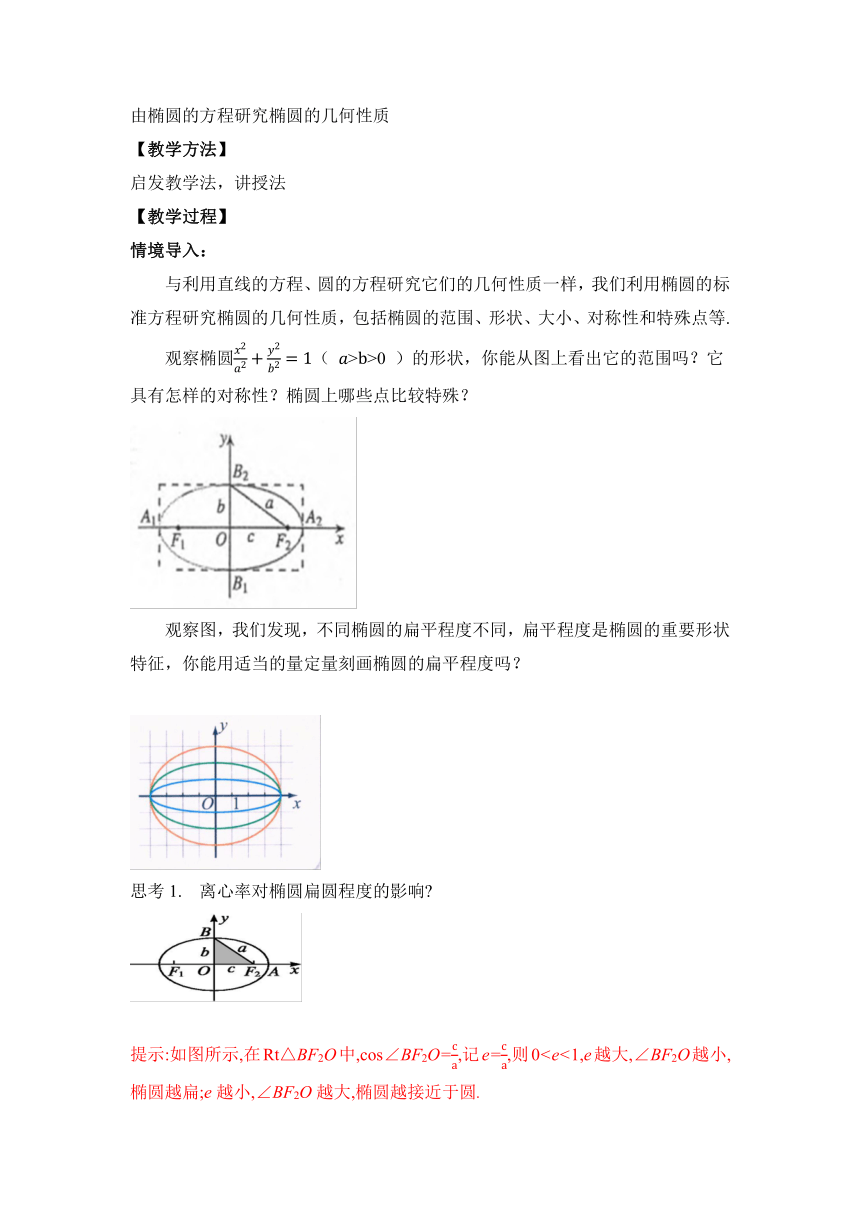
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
观察椭圆( >>0 )的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
思 观察图,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
思考1. 离心率对椭圆扁圆程度的影响
提示:如图所示,在Rt△BF2O中,cos∠BF2O=,记e=,则0知识精讲:
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a), B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c
对称性 对称轴:x轴、y轴,对称中心:坐标原点
离心率
课堂练习:
1.判断
(1)椭圆=1(a>b>0)的长轴长是a. ( )
(2)若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的方程为=1. ( )
(3)设F为椭圆=1(a>b>0)的一个焦点,M为其上任一点,则|MF|的最大值为a+c(c为椭圆的半焦距). ( )
答案:(1)× (2)× (3)√
2.已知椭圆C:=1的一个焦点为(2,0),则C的离心率为( )
A. B. C. D.
解析:∵a2=4+22=8,∴a=2.∴e=.故选C.
答案:C
典例精析:
例1已知椭圆C1:=1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的半长轴长、半短轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
解:(1)由椭圆C1:=1,可得其半长轴长为10,半短轴长为8,焦点坐标为(6,0),(-6,0),离心率e=.
(2)椭圆C2:=1.性质如下:
①范围:-8≤x≤8且-10≤y≤10;②对称性:关于x轴、y轴、原点对称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0);④焦点:(0,6),(0,-6);⑤离心率:e=.
归纳总结:
讨论椭圆的几何性质时,一定要将方程化为标准方程,标准方程能将参数的几何意义凸显出来,另外要抓住椭圆中a2-b2=c2这一核心关系式.
课堂练习:
跟踪训练1 求椭圆m2x2+4m2y2=1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.
解:由已知得=1(m>0),因为0所以椭圆的焦点在x轴上,并且半长轴长a=,
半短轴长b=,半焦距c=,
所以椭圆的长轴长2a=,短轴长2b=,
焦点坐标为,
顶点坐标为,
离心率e=.
典例精析:
例2 椭圆=1(a>b>0)的两焦点为F1,F2,以F1F2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为 .
解析:方法一:如图,∵△DF1F2为正三角形,N为DF2的中点,
∴F1N⊥F2N.∵|NF2|=|OF2|=c,
∴|NF1|=c.
由椭圆的定义可知|NF1|+|NF2|=2a,
∴c+c=2a,∴a=.
∴e=-1.
方法二:注意到焦点三角形NF1F2中,∠NF1F2=30°,∠NF2F1=60°,∠F1NF2=90°,
则由离心率的焦点三角形公式,
可得e=-1.
答案:-1
课堂练习:
跟踪训练2. 若例2改为如下:椭圆=1(a>b>0)的两焦点F1,F2,以F1F2为底边作等腰直角三角形,其三角形顶点恰好落在椭圆的顶点处,则椭圆的离心率为 .
解析:根据等腰直角三角形的特征可知a2+a2=4c2,即=e=.
答案:
典例精析:
例3 已知椭圆=1(a>b>0),F1,F2分别是椭圆的左、右焦点,椭圆上总存在点P使得PF1⊥PF2,则椭圆的离心率的取值范围为 .
解析:由PF1⊥PF2,知△F1PF2是直角三角形,所以|OP|=c≥b,即c2≥a2-c2,
所以a≤c.因为e=,0答案:
归纳总结:
求椭圆离心率的值或取值范围的常用方法
(1)直接法:若已知a,c,可直接利用e=求解.若已知a,b(或b,c)可借助于a2=b2+c2求出c(或a),再代入公式e=求解.
(2)几何法:若借助数形结合,可挖掘涉及几何图形的性质,再借助a2=b2+c2,找到a与c的关系或求出a与c,代入e=即可得到.
(3)方程法:若a,c的值不可求,则可根据条件建立关于a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围).
课堂练习:
跟踪训练3. (1)已知椭圆=1(a>b>0)过点(1,),其离心率的取值范围是,则椭圆短轴长的最大值是( )
A.4 B.3 C. D.2
解析:(1)由题意,可得=1,即a2=.因为a2=b2+c2,
所以=3-b2,离心率的取值范围是,
所以≤3-b2≤,解得b∈,所以椭圆短轴长的最大值是.
(2)设F1,F2分别是椭圆E:=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为 .
解析:(2)由题意,知∠F2F1P=∠F2PF1=30°,
∴∠PF2x=60°.∴|PF2|=2×=3a-2c.
∵|F1F2|=2c,|F1F2|=|PF2|,∴3a-2c=2c,∴e=.
答案:(1)C (2)
(3)已知椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若椭圆C的中心到直线AB的距离为|F1F2|,求椭圆C的离心率.
解析:(3)由题意知A(a,0),B(0,b),
从而直线AB的方程为=1,即bx+ay-ab=0,又|F1F2|=2c,∴c.
∵b2=a2-c2,∴3a4-7a2c2+2c4=0,解得a2=2c2或3a2=c2(舍去),∴e=.
典例精析:
例4. 如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口 ABC是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位另一个焦点上,由椭圆一个焦点 发出的光线,经过旋转椭圆面反射后集中到另一个椭圆焦点,已知,=2.8cm, =4.5cm,试建立适当的平面直角坐标系,求截口ABC所在的椭圆方程(精确到0.1cm)
解:建立如图所示的平面直角坐标系,设所求椭圆方程为
(>>0)
在Rt 中,
=
有椭圆的性质 , =2所以
)=)
所以所求椭圆方程为
归纳总结:
利用椭圆的几何性质求标准方程的思路
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
课堂练习:
跟踪训练4.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
A.+=1 B.+=1 C.+=1 D.+=1
【解析】B [由题意,得解得
因为椭圆的焦点在x轴上,
所以椭圆的标准方程为+=1.]
达标检测:
1.已知点(3,2)在椭圆=1上,则( )
A.点(-3,-2)不在椭圆上
B.点(3,-2)不在椭圆上
C.点(-3,2)在椭圆上
D.无法判断点(-3,-2),(3,-2),(-3,2)是否在椭圆上
解析:由椭圆以坐标轴为对称轴,以原点为对称中心可知,点(-3,2)在椭圆上,故选C.
答案:C
2.设AB是椭圆=1(a>b>0)的长轴,若把线段AB分为100等份,过每个分点作AB的垂线,分别交椭圆的上半部分于点P1,P2,…,P99,F1为椭圆的左焦点,则
|F1A|+|F1P1|+|F1P2|+…+|F1P99|+|F1B|的值是( )
A.98a B.99a C.100a D.101a
解析:由椭圆的定义及其对称性可知|F1P1|+|F1P99|=|F1P2|+|F1P98|=…=|F1P49|+|F1P51|=|F1A|+|F1B|=2a,|F1P50|=a,故结果应为50×2a+|F1P50|=101a.
答案:D
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( )
A. B. C. D.
解析:不妨设椭圆的左、右焦点分别为F1,F2,B为椭圆的上顶点.依题意可知,
△BF1F2是正三角形.∵在Rt△OBF2中,|OF2|=c,|BF2|=a,∠OF2B=60°,
∴cos 60°=.即椭圆的离心率e=,故选A.
答案:A
4.已知椭圆=1左、右焦点分别为F1,F2,上、下顶点分别为B1,B2,则四边形B1F1B2F2的面积为 .
解析:根据题意,设四边形B1F1B2F2的面积为S,
椭圆的标准方程为=1,其中a=,b=,
则c==1,
则F1(-1,0),F2(1,0),B1(0,),B2(0,-),
即|OF1|=|OF2|=1,|OB1|=|OB2|=,
则S=4×=4××|OB1|×|OF1|=2.
答案:2
5.万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆.已知大椭圆的长轴长为40 cm,短轴长为20 cm,小椭圆的短轴长为10 cm,则小椭圆的长轴长为 cm.
解析:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
,即.所以,所以,
所以小椭圆的长轴长为20 cm.
答案:20
6.已知椭圆x2+(m+3)y2=m(m>0)的离心率e=,求m的值及椭圆的长轴长、短轴长、焦点坐标、顶点坐标.
解:椭圆方程可化为=1(m>0),
∵m->0,∴m>.
∴a2=m,b2=,c=.由e=,得,∴m=1.
∴椭圆的标准方程为x2+=1.∴a=1,b=,c=.∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为;四个顶点坐标分别为(-1,0),(1,0),.
7. 求满足下列条件的椭圆的标准方程:
(1)焦点在y轴上,焦距是4,且经过点M(3,2);
(2)c∶a=5∶13,且椭圆上一点到两焦点的距离的和为26.
【答案】(1) (2)或(3)
【解析】(1)由焦距是4,可得c=2,且焦点坐标为(0,-2),(0,2).由椭圆的定义知,,所以a=4,
所以b2=a2-c2=16-4=12.
又焦点在y轴上,所以椭圆的标准方程为.
(2)由题意知,2a=26,即a=13,又因为c∶a=5∶13,所以c=5,
所以b2=a2-c2=132-52=144,因为焦点所在的坐标轴不确定,
所以椭圆的标准方程为或.
【课后小结】
【板书设计】
【教学反思】
运用代数方法,让学生体会方程与函数的思想在研究椭圆几何性质中的作用,让学生的思路更加清晰,对学习内容的把握更加容易,同时注意及时让学生进行思维拓展,形成知识网,提升教学效果.
《3.1.2椭圆的简单几何性质(1)》教学设计
【教材分析】
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习椭圆的简单几何性质,教材的地位和作用地位:本节课是在椭圆的概念和标准方程的基础上,运用代数的方法,研究椭圆的简单几何性质及简单应用 . 本节课内容的掌握程度直接影响学习双曲线和抛物线几何性质.作用:提高学生的数学素质,培养学生的数形结合思想,及分析问题和解决问题的能力.因此,内容在解析几何中占有非常重要的地位.
【学情分析】
椭圆是高中数学课程内容中较难的一章节,需要学生具备良好的解析几何思维以及综合计算能力,通过学习椭圆,理解其几何意义,掌握其标准方程和几何性质,并会综合应用解决问题,在本节课程学习中,要注重学生对概念的理解,从简单的题目入手,直接应用性质解题,循序渐进,逐步掌握综合应用题目的解题思路和方法.
【教学目标与核心素养】
教学目标:
A. 掌握椭圆的几何性质,掌握a,b,c,e的几何意义及a,b,c,e之间的相互关系.
B.尝试利用椭圆的方程研究椭圆的几何性质.
C.尝试利用椭圆的知识解决简单的实际问题.
核心素养:
1.数学抽象:椭圆的几何性质
2.逻辑推理:利用椭圆的方程研究椭圆的几何性
3.数学运算:利用椭圆的方程研究椭圆的几何性
4.数学建模:利用椭圆的知识解决应用问题
5.直观想象:离心率的几何意义
【教学重点】
由几何条件求出椭圆的方程
【教学难点】
由椭圆的方程研究椭圆的几何性质
【教学方法】
启发教学法,讲授法
【教学过程】
情境导入:
与利用直线的方程、圆的方程研究它们的几何性质一样,我们利用椭圆的标准方程研究椭圆的几何性质,包括椭圆的范围、形状、大小、对称性和特殊点等.
观察椭圆( >>0 )的形状,你能从图上看出它的范围吗?它具有怎样的对称性?椭圆上哪些点比较特殊?
思 观察图,我们发现,不同椭圆的扁平程度不同,扁平程度是椭圆的重要形状特征,你能用适当的量定量刻画椭圆的扁平程度吗?
思考1. 离心率对椭圆扁圆程度的影响
提示:如图所示,在Rt△BF2O中,cos∠BF2O=,记e=,则0
椭圆的几何性质
焦点的位置 焦点在x轴上 焦点在y轴上
图形
标准 方程
焦点的位置 焦点在x轴上 焦点在y轴上
范围 -a≤x≤a且-b≤y≤b -b≤x≤b且-a≤y≤a
顶点 A1(-a,0),A2(a,0), B1(0,-b),B2(0,b) A1(0,-a),A2(0,a), B1(-b,0),B2(b,0)
轴长 长轴长为2a,短轴长为2b
焦点 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
焦距 2c
对称性 对称轴:x轴、y轴,对称中心:坐标原点
离心率
课堂练习:
1.判断
(1)椭圆=1(a>b>0)的长轴长是a. ( )
(2)若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的方程为=1. ( )
(3)设F为椭圆=1(a>b>0)的一个焦点,M为其上任一点,则|MF|的最大值为a+c(c为椭圆的半焦距). ( )
答案:(1)× (2)× (3)√
2.已知椭圆C:=1的一个焦点为(2,0),则C的离心率为( )
A. B. C. D.
解析:∵a2=4+22=8,∴a=2.∴e=.故选C.
答案:C
典例精析:
例1已知椭圆C1:=1,设椭圆C2与椭圆C1的长轴长、短轴长分别相等,且椭圆C2的焦点在y轴上.
(1)求椭圆C1的半长轴长、半短轴长、焦点坐标及离心率;
(2)写出椭圆C2的方程,并研究其性质.
解:(1)由椭圆C1:=1,可得其半长轴长为10,半短轴长为8,焦点坐标为(6,0),(-6,0),离心率e=.
(2)椭圆C2:=1.性质如下:
①范围:-8≤x≤8且-10≤y≤10;②对称性:关于x轴、y轴、原点对称;③顶点:长轴端点(0,10),(0,-10),短轴端点(-8,0),(8,0);④焦点:(0,6),(0,-6);⑤离心率:e=.
归纳总结:
讨论椭圆的几何性质时,一定要将方程化为标准方程,标准方程能将参数的几何意义凸显出来,另外要抓住椭圆中a2-b2=c2这一核心关系式.
课堂练习:
跟踪训练1 求椭圆m2x2+4m2y2=1(m>0)的长轴长、短轴长、焦点坐标、顶点坐标和离心率.
解:由已知得=1(m>0),因为0
半短轴长b=,半焦距c=,
所以椭圆的长轴长2a=,短轴长2b=,
焦点坐标为,
顶点坐标为,
离心率e=.
典例精析:
例2 椭圆=1(a>b>0)的两焦点为F1,F2,以F1F2为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为 .
解析:方法一:如图,∵△DF1F2为正三角形,N为DF2的中点,
∴F1N⊥F2N.∵|NF2|=|OF2|=c,
∴|NF1|=c.
由椭圆的定义可知|NF1|+|NF2|=2a,
∴c+c=2a,∴a=.
∴e=-1.
方法二:注意到焦点三角形NF1F2中,∠NF1F2=30°,∠NF2F1=60°,∠F1NF2=90°,
则由离心率的焦点三角形公式,
可得e=-1.
答案:-1
课堂练习:
跟踪训练2. 若例2改为如下:椭圆=1(a>b>0)的两焦点F1,F2,以F1F2为底边作等腰直角三角形,其三角形顶点恰好落在椭圆的顶点处,则椭圆的离心率为 .
解析:根据等腰直角三角形的特征可知a2+a2=4c2,即=e=.
答案:
典例精析:
例3 已知椭圆=1(a>b>0),F1,F2分别是椭圆的左、右焦点,椭圆上总存在点P使得PF1⊥PF2,则椭圆的离心率的取值范围为 .
解析:由PF1⊥PF2,知△F1PF2是直角三角形,所以|OP|=c≥b,即c2≥a2-c2,
所以a≤c.因为e=,0
归纳总结:
求椭圆离心率的值或取值范围的常用方法
(1)直接法:若已知a,c,可直接利用e=求解.若已知a,b(或b,c)可借助于a2=b2+c2求出c(或a),再代入公式e=求解.
(2)几何法:若借助数形结合,可挖掘涉及几何图形的性质,再借助a2=b2+c2,找到a与c的关系或求出a与c,代入e=即可得到.
(3)方程法:若a,c的值不可求,则可根据条件建立关于a,b,c的关系式,借助于a2=b2+c2,转化为关于a,c的齐次方程(或不等式),再将方程(或不等式)两边同除以a的最高次幂,得到关于e的方程(或不等式),即可求得e的值(或取值范围).
课堂练习:
跟踪训练3. (1)已知椭圆=1(a>b>0)过点(1,),其离心率的取值范围是,则椭圆短轴长的最大值是( )
A.4 B.3 C. D.2
解析:(1)由题意,可得=1,即a2=.因为a2=b2+c2,
所以=3-b2,离心率的取值范围是,
所以≤3-b2≤,解得b∈,所以椭圆短轴长的最大值是.
(2)设F1,F2分别是椭圆E:=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为 .
解析:(2)由题意,知∠F2F1P=∠F2PF1=30°,
∴∠PF2x=60°.∴|PF2|=2×=3a-2c.
∵|F1F2|=2c,|F1F2|=|PF2|,∴3a-2c=2c,∴e=.
答案:(1)C (2)
(3)已知椭圆C:=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若椭圆C的中心到直线AB的距离为|F1F2|,求椭圆C的离心率.
解析:(3)由题意知A(a,0),B(0,b),
从而直线AB的方程为=1,即bx+ay-ab=0,又|F1F2|=2c,∴c.
∵b2=a2-c2,∴3a4-7a2c2+2c4=0,解得a2=2c2或3a2=c2(舍去),∴e=.
典例精析:
例4. 如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分.过对称轴的截口 ABC是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位另一个焦点上,由椭圆一个焦点 发出的光线,经过旋转椭圆面反射后集中到另一个椭圆焦点,已知,=2.8cm, =4.5cm,试建立适当的平面直角坐标系,求截口ABC所在的椭圆方程(精确到0.1cm)
解:建立如图所示的平面直角坐标系,设所求椭圆方程为
(>>0)
在Rt 中,
=
有椭圆的性质 , =2所以
)=)
所以所求椭圆方程为
归纳总结:
利用椭圆的几何性质求标准方程的思路
利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:
(1)确定焦点位置;
(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);
(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.
课堂练习:
跟踪训练4.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,一个焦点的坐标是(3,0),则椭圆的标准方程为( )
A.+=1 B.+=1 C.+=1 D.+=1
【解析】B [由题意,得解得
因为椭圆的焦点在x轴上,
所以椭圆的标准方程为+=1.]
达标检测:
1.已知点(3,2)在椭圆=1上,则( )
A.点(-3,-2)不在椭圆上
B.点(3,-2)不在椭圆上
C.点(-3,2)在椭圆上
D.无法判断点(-3,-2),(3,-2),(-3,2)是否在椭圆上
解析:由椭圆以坐标轴为对称轴,以原点为对称中心可知,点(-3,2)在椭圆上,故选C.
答案:C
2.设AB是椭圆=1(a>b>0)的长轴,若把线段AB分为100等份,过每个分点作AB的垂线,分别交椭圆的上半部分于点P1,P2,…,P99,F1为椭圆的左焦点,则
|F1A|+|F1P1|+|F1P2|+…+|F1P99|+|F1B|的值是( )
A.98a B.99a C.100a D.101a
解析:由椭圆的定义及其对称性可知|F1P1|+|F1P99|=|F1P2|+|F1P98|=…=|F1P49|+|F1P51|=|F1A|+|F1B|=2a,|F1P50|=a,故结果应为50×2a+|F1P50|=101a.
答案:D
3.若椭圆的两个焦点与短轴的一个端点构成一个正三角形,则该椭圆的离心率为( )
A. B. C. D.
解析:不妨设椭圆的左、右焦点分别为F1,F2,B为椭圆的上顶点.依题意可知,
△BF1F2是正三角形.∵在Rt△OBF2中,|OF2|=c,|BF2|=a,∠OF2B=60°,
∴cos 60°=.即椭圆的离心率e=,故选A.
答案:A
4.已知椭圆=1左、右焦点分别为F1,F2,上、下顶点分别为B1,B2,则四边形B1F1B2F2的面积为 .
解析:根据题意,设四边形B1F1B2F2的面积为S,
椭圆的标准方程为=1,其中a=,b=,
则c==1,
则F1(-1,0),F2(1,0),B1(0,),B2(0,-),
即|OF1|=|OF2|=1,|OB1|=|OB2|=,
则S=4×=4××|OB1|×|OF1|=2.
答案:2
5.万众瞩目的北京冬奥会将于2022年2月4日正式开幕,继2008年北京奥运会之后,国家体育场(又名鸟巢)将再次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是两个大小不同、扁平程度相同的椭圆.已知大椭圆的长轴长为40 cm,短轴长为20 cm,小椭圆的短轴长为10 cm,则小椭圆的长轴长为 cm.
解析:因为两个椭圆的扁平程度相同,所以椭圆的离心率相同,
,即.所以,所以,
所以小椭圆的长轴长为20 cm.
答案:20
6.已知椭圆x2+(m+3)y2=m(m>0)的离心率e=,求m的值及椭圆的长轴长、短轴长、焦点坐标、顶点坐标.
解:椭圆方程可化为=1(m>0),
∵m->0,∴m>.
∴a2=m,b2=,c=.由e=,得,∴m=1.
∴椭圆的标准方程为x2+=1.∴a=1,b=,c=.∴椭圆的长轴长为2,短轴长为1;两焦点坐标分别为;四个顶点坐标分别为(-1,0),(1,0),.
7. 求满足下列条件的椭圆的标准方程:
(1)焦点在y轴上,焦距是4,且经过点M(3,2);
(2)c∶a=5∶13,且椭圆上一点到两焦点的距离的和为26.
【答案】(1) (2)或(3)
【解析】(1)由焦距是4,可得c=2,且焦点坐标为(0,-2),(0,2).由椭圆的定义知,,所以a=4,
所以b2=a2-c2=16-4=12.
又焦点在y轴上,所以椭圆的标准方程为.
(2)由题意知,2a=26,即a=13,又因为c∶a=5∶13,所以c=5,
所以b2=a2-c2=132-52=144,因为焦点所在的坐标轴不确定,
所以椭圆的标准方程为或.
【课后小结】
【板书设计】
【教学反思】
运用代数方法,让学生体会方程与函数的思想在研究椭圆几何性质中的作用,让学生的思路更加清晰,对学习内容的把握更加容易,同时注意及时让学生进行思维拓展,形成知识网,提升教学效果.
