八年级数学上册沪教版17.4一元二次方程的应用—实际问题(第2课时)(共26张PPT)
文档属性
| 名称 | 八年级数学上册沪教版17.4一元二次方程的应用—实际问题(第2课时)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 863.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 19:31:17 | ||
图片预览








文档简介
(共26张PPT)
沪教版八年级上册
第 17 章一元二次方程
17.4一元二次方程的应用—实际问题(第2课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
1.会分析几何问题、增长率问题中的数量关系,并通过列一元二次方程解决实际问题.
2.在应用一元二次方程解决实际问题的探索活动中,增强数学应用意识,激发学习兴趣,学会观察问题、分析问题、解决问题的能力.
(2)增长率问题:设基数为a,平均增长率为x(x是一个百分数),则第一次增长后为a(1+x),第二次是在第一次增长后的基础上的再增长,此时基数已变为a(1+x),故第二次增长后为a(1+x)2.
一块长方形绿地,管理员告诉麦兜这块地的面积为1200平方米,并且长比宽多10米,麦兜想:那么长和宽各为多少?
如果设绿地宽为x米,则长为_____米。由题意得方程:___________;解得__________
X+10
X(X+10)=1200
X1=30,x2=-40
宽是30米和
-40米吗?
经检验x= -40不合题意,当X=30时X+10=40
答:长是40米,宽是30米
1.几何图形面积
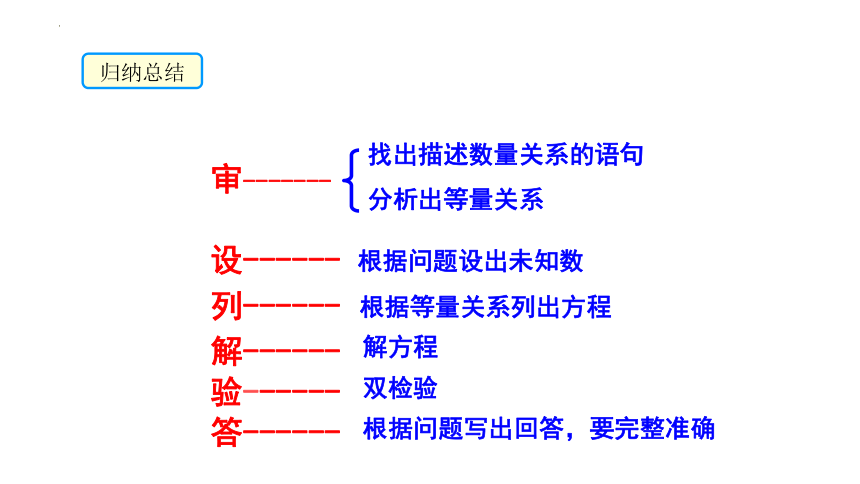
审-------
根据问题设出未知数
设------
根据等量关系列出方程
列------
解方程
双检验
根据问题写出回答,要完整准确
解------
验------
答------
找出描述数量关系的语句
分析出等量关系
归纳总结
例1.(1)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为1152平方米,那么长方形两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=1152 x2-60x+576=0
解得x1=12,x2=48
经检验x1,x2都符合实际意义。
当x=12时,120-2x=96 当x=48时,120-2x=24
答:长方行鸡场的两边是96米和12米或24米和48米。
例1.(2)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为1800平方米,那么长方形鸡场的两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=1800
x2-60x+900=0
解得x1=x2=30
经检验x=30符合实际意义。
当x=30时,120-2x=60
答:长方行鸡场的两边是30米和60米。
例1.(3)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为2000平方米,那么长方形鸡场的两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=2000
x2-60x+1000=0
⊿=-400﹤0,所以方程无实数根。
答:用120米长的铁栅栏不能围成按题中要求的面积是2000平方米的鸡场。
例2.某工厂七月份产值是100万元,计划九月份要达到144万元,如果每年的增长率相同,求这个增长率。
这个增长率是多少呢?
2.增长率
最后产值M、基数a、平均增长率(或降低率)x、增长(或降低)次数 n的关系:
M=a(1±x)n
例2.某工厂七月份产值是100万元,计划九月份要达到144万元,如果每年的增长率相同,求这个增长率。
解 设这个工厂每月产值的增长率为 x.根据题意,得方程
答:这个工厂八、九两月的月增长率为 20%.
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
课本练习
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
2.某种产品原来每件价格为 800 元,经过两次降价,且每次降价的百分率相同,现在每件售价为 578 元,求每次降价的百分率
1.某品牌手机三月份销售400万部,四月份、五月份销售量
连续增长,五月份销售量达到900万部,求月平均增长率.
设月平均增长率为x,根据题意列方程为( )
A.400(1+x2)=900 B.400(1+2x)=900
C.900(1-x)2=400 D.400(1+x)2=900
D
随堂检测
A
4
2
5.【易错题】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮的传播就会有144台电脑被感染,则每轮感染中平均一台电脑会感染________台电脑.
11
6.2017年,某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2019年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2020年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
解:(1)设平均每年下调的百分率为x.根据题意,
得6500·(1-x)2=5265,解得x1=0.1=10%,x2=1.9(舍去).
故平均每年下调的百分率为10%.
(2)如果下调的百分率相同,
则2020年的房价为5265×(1-10%)=4738.5(元/平方米),
则100平方米的住房总房款为100×4738.5=473 850(元)=47.385(万元).
∵20+30>47.385,
∴张强的愿望可以实现.
8.李明准备进行如下操作实验:把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的想法正确吗?请说明理由.
9.如图,Rt△ABC中,∠B=90°,AC=10 cm,BC=6 cm.现有两个动点P、Q分别从点A和点B同时出发,其中点P以2 cm/s的速度沿AB向终点B移动;点Q以1 cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x s.
(1)用含x的代数式表示PB和BQ的值;
(2)是否存在x的值,使得四边形APQC的面积等于20 cm2?若存在,请求出此时x的值;若不存在,请说明理由.
沪教版八年级上册
第 17 章一元二次方程
17.4一元二次方程的应用—实际问题(第2课时)
目 录
1 学习目标
2 新课讲解
3 课本例题
4 课本练习
6 随堂检测
7 课堂小结
5 题型讲解
学习目标
1.会分析几何问题、增长率问题中的数量关系,并通过列一元二次方程解决实际问题.
2.在应用一元二次方程解决实际问题的探索活动中,增强数学应用意识,激发学习兴趣,学会观察问题、分析问题、解决问题的能力.
(2)增长率问题:设基数为a,平均增长率为x(x是一个百分数),则第一次增长后为a(1+x),第二次是在第一次增长后的基础上的再增长,此时基数已变为a(1+x),故第二次增长后为a(1+x)2.
一块长方形绿地,管理员告诉麦兜这块地的面积为1200平方米,并且长比宽多10米,麦兜想:那么长和宽各为多少?
如果设绿地宽为x米,则长为_____米。由题意得方程:___________;解得__________
X+10
X(X+10)=1200
X1=30,x2=-40
宽是30米和
-40米吗?
经检验x= -40不合题意,当X=30时X+10=40
答:长是40米,宽是30米
1.几何图形面积
审-------
根据问题设出未知数
设------
根据等量关系列出方程
列------
解方程
双检验
根据问题写出回答,要完整准确
解------
验------
答------
找出描述数量关系的语句
分析出等量关系
归纳总结
例1.(1)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为1152平方米,那么长方形两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=1152 x2-60x+576=0
解得x1=12,x2=48
经检验x1,x2都符合实际意义。
当x=12时,120-2x=96 当x=48时,120-2x=24
答:长方行鸡场的两边是96米和12米或24米和48米。
例1.(2)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为1800平方米,那么长方形鸡场的两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=1800
x2-60x+900=0
解得x1=x2=30
经检验x=30符合实际意义。
当x=30时,120-2x=60
答:长方行鸡场的两边是30米和60米。
例1.(3)某建筑工程队,在工地一边的靠墙处,用120米长的铁栅栏围一个所占地面为长方形的临时仓库,铁栅栏只围三边,长方形面积为2000平方米,那么长方形鸡场的两边长各为多少?
x
120-2x
解:设垂直于墙面的一边长为x米,则平行于墙面的一边长为(120-2x)米。
x(120-2x)=2000
x2-60x+1000=0
⊿=-400﹤0,所以方程无实数根。
答:用120米长的铁栅栏不能围成按题中要求的面积是2000平方米的鸡场。
例2.某工厂七月份产值是100万元,计划九月份要达到144万元,如果每年的增长率相同,求这个增长率。
这个增长率是多少呢?
2.增长率
最后产值M、基数a、平均增长率(或降低率)x、增长(或降低)次数 n的关系:
M=a(1±x)n
例2.某工厂七月份产值是100万元,计划九月份要达到144万元,如果每年的增长率相同,求这个增长率。
解 设这个工厂每月产值的增长率为 x.根据题意,得方程
答:这个工厂八、九两月的月增长率为 20%.
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
课本练习
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
1.用100 厘米长的铅丝,弯折一个长方形的模型.分别在下列条件下,求相邻两边的长:
(1)长方形的面积是 525 平方厘米:
(2)长方形的面积是 625 平方厘米:
(3)长方形的面积是 700 平方厘米.
2.某种产品原来每件价格为 800 元,经过两次降价,且每次降价的百分率相同,现在每件售价为 578 元,求每次降价的百分率
1.某品牌手机三月份销售400万部,四月份、五月份销售量
连续增长,五月份销售量达到900万部,求月平均增长率.
设月平均增长率为x,根据题意列方程为( )
A.400(1+x2)=900 B.400(1+2x)=900
C.900(1-x)2=400 D.400(1+x)2=900
D
随堂检测
A
4
2
5.【易错题】某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮的传播就会有144台电脑被感染,则每轮感染中平均一台电脑会感染________台电脑.
11
6.2017年,某楼盘以每平方米6500元的均价对外销售.因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2019年的均价为每平方米5265元.
(1)求平均每年下调的百分率;
(2)假设2020年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款30万元,张强的愿望能否实现?(房价每平方米按照均价计算)
解:(1)设平均每年下调的百分率为x.根据题意,
得6500·(1-x)2=5265,解得x1=0.1=10%,x2=1.9(舍去).
故平均每年下调的百分率为10%.
(2)如果下调的百分率相同,
则2020年的房价为5265×(1-10%)=4738.5(元/平方米),
则100平方米的住房总房款为100×4738.5=473 850(元)=47.385(万元).
∵20+30>47.385,
∴张强的愿望可以实现.
8.李明准备进行如下操作实验:把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的想法正确吗?请说明理由.
9.如图,Rt△ABC中,∠B=90°,AC=10 cm,BC=6 cm.现有两个动点P、Q分别从点A和点B同时出发,其中点P以2 cm/s的速度沿AB向终点B移动;点Q以1 cm/s的速度沿BC向终点C移动,其中一点到终点,另一点也随之停止.连结PQ,设动点运动时间为x s.
(1)用含x的代数式表示PB和BQ的值;
(2)是否存在x的值,使得四边形APQC的面积等于20 cm2?若存在,请求出此时x的值;若不存在,请说明理由.
