3.1.1椭圆及其标准方程 课件(共51张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 14:09:12 | ||
图片预览









文档简介
(共51张PPT)
人教A版数学选择性必修第一册
3.1.1椭圆及其标准方程
1.理解椭圆的定义及椭圆的标准方程.(重点)
2.掌握用定义法和待定系数法求椭圆的标准方程.(重点)
3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题.(难点)
椭圆是圆锥曲线的一种具有丰富的几何性质,在科研生产和人类生活中具有广泛的应用,那么椭圆到底有怎样的几何性质,我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础。
取一条定长的细线,把它的两端都固定在图板
的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆。如果把细绳的两端拉开一段距离,分别固定在图板中的两点F1,F2 ,
套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
常数(大于|F1F2|)
两个定点
两焦点间的距离
一半
观察椭圆的形状,你认为怎样建立坐标系可能使所得的椭圆方程形式简单?
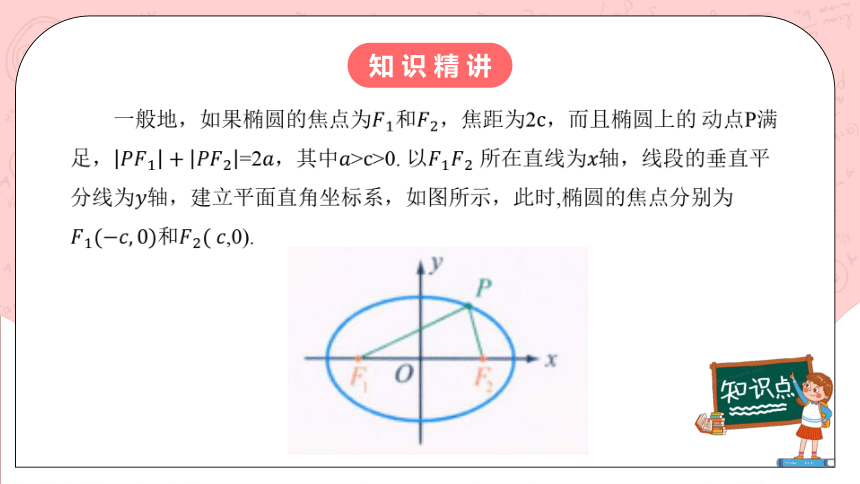
一般地,如果椭圆的焦点为,焦距为2,而且椭圆上的 动点P满足,=2,其中>>0. 以 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示,此时,椭圆的焦点分别为 ,0).
=2. ①
①,我们将其左边一个根式移到右边,得
对方程两边平方,得=
整理,得= ③
对方程③两边平方,得=
整理得 ④
将方程④两边同除以,得 ⑤
由椭圆的定义可知>>0 ,即>>0,所以.
观察图,你能从中找出表示,的线段吗?
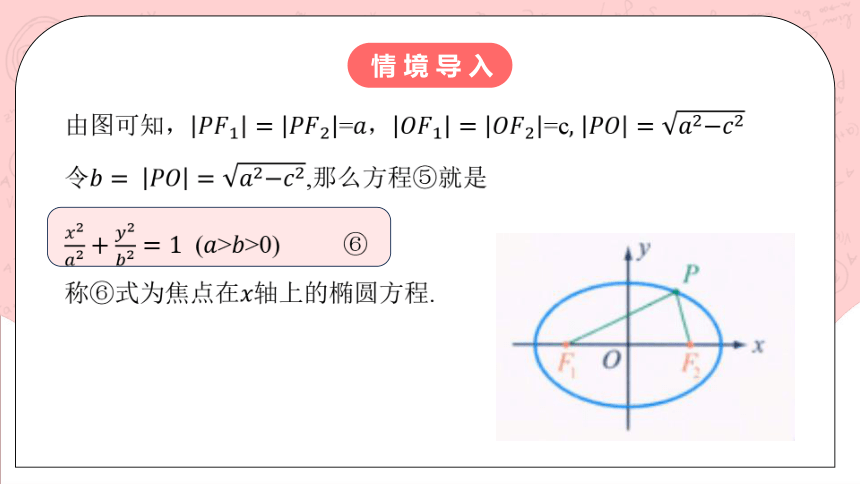
由图可知,=,=c
令,那么方程⑤就是
(>>0) ⑥
称⑥式为焦点在轴上的椭圆方程.
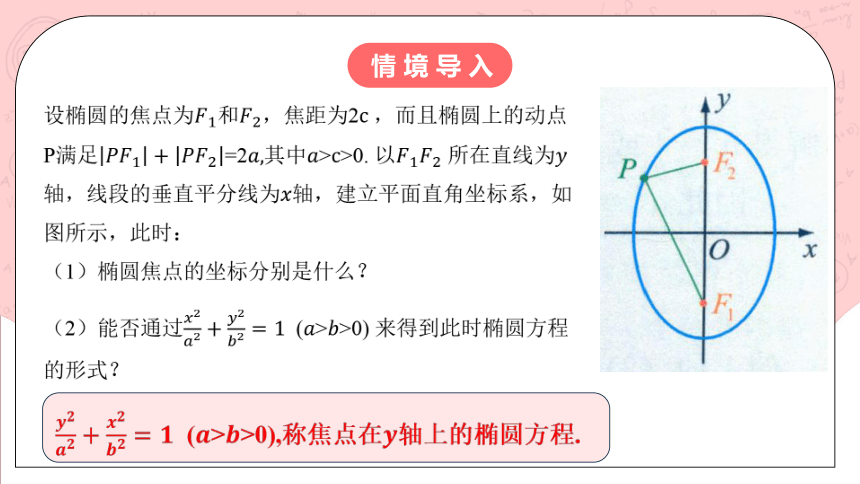
设椭圆,焦距为2,而且椭圆上的动点P满足=2其中>>0. 以 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示,此时:
(1)椭圆焦点的坐标分别是什么?
(2)能否通过 (>>0) 来得到此时椭圆方程的形式?
(>>0),称焦点在轴上的椭圆方程.
2.椭圆的标准方程
焦点在x轴上 焦点在y轴上
标准 方程
图形
焦点坐标 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
a,b,c关系 b2=a2-c2
1. a=6,c=1的椭圆的标准方程是( )
A.=1 B.=1 C.=1 D.=1或=1
2. 椭圆+y2=1上一点P到一个焦点的距离为2,则点P到另一个焦点的距离为( )
A.5 B.6 C.7 D.8
3. 椭圆4x2+9y2=1的焦点坐标是( )
A.(±,0) B.(0,±) C. D.
解析: (1) 易得为D选项.
(2)设椭圆的左、右焦点分别为F1,F2,若|PF1|=2,
结合椭圆定义|PF2|+|PF1|=10,可得|PF2|=8.
答案:(1)D (2)D (3)C
例1. 已知 是定点,.若动点满足,则动点的轨迹是( )
直线 B.线段 C.圆 D.椭圆
【答案】B
【解析】对于在平面内,若动点到、两点的距离之和等于6,而6正好等于两定点、的距离,则动点的轨迹是以,为端点的线段.
故选:B.
椭圆是在平面内定义的,所以“平面内”这一条件不能忽视.
定义中到两定点的距离之和是常数,而不能是变量.
常数(2a)必须大于两定点间的距离,否则轨迹不是椭圆,这是判断曲线是否为椭圆的限制条件.
跟踪训练1.若椭圆上一点P到左焦点的距离为5,则其到右焦点的距离为( )
A.5 B.3 C.2 D.1
【答案】D
【解析】由题意a=3,P点到右焦点的距离为2a-5=1.
例2.(1)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B.(0,2) C. D.
(2)方程表示椭圆,则实数的取值范围( )
A. B. C. D.且
【答案】(1)A(2)D
【解析】(1)转化为椭圆的标准方程,得,因为表示焦点在轴上的椭圆,所以,解得.所以实数的取值范围是.选A.
(2)方程表示椭圆,若焦点在x轴上,;若焦点在y轴上,.综上:实数的取值范围是且,故选:D
把方程写成椭圆的标准方程形式,得到形式,要想表示
焦点在轴上的椭圆,必须要满足,解这个不等式就可求出实数的取值范围.
焦点在x轴上的椭圆,必须要满足A>B>0,解这个不等式就可求出实数的取值范围.
椭圆,必须要满足解这个不等式就可求出实数的取值范围.
跟踪训练2.“”是“方程表示椭圆”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】因为方程表示椭圆的充要条件是,
即且,故“”是“方程表示椭圆”的必要而不充分条件.故选:B.
例3.(1)已知的顶点,在椭圆上,顶点是椭圆的一个焦点,且椭圆的另一个焦点在上,则的周长是( )
A. B. C. D.
(2)已知是椭圆上一点, 为椭圆的两焦点,且,则面积为( )
A. B. C. D.
【答案】(1)C (2)A
【解析】(1)的顶点,在椭圆上,顶点是椭圆的一个焦点,且椭圆的另一个焦点在上,由椭圆的定义可得:的周长是.故选:C.
(2)由椭圆的标准方程可得:a=5,b=3,∴c=4,
设|PF1|=t1,|PF2|=t2,所以根据椭圆的定义可得:t1+t2=10①,
在△F1PF2中,∠F1PF2=60°,所以根据余弦定理可得:
|PF1|2+|PF2|2﹣2|PF1||PF2|cos60°=|F1F2|2=(2c)2=64,
整理可得:t12+t22﹣t1t2=64,②把①两边平方得t12+t22+2t1 t2=100,③
所以③﹣②得t1t2=12,∴∠F1PF2=3.故选A.
跟踪训练3.已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【答案】C
【解析】根据椭圆方程可知,根据椭圆的定义可知,的周长为,故选C.
(3)动点到定点的距离和到定直线的距离之比是常数,求动点点的轨迹.
【解】(1)答案x2+=1 解析:设Q(x,y),P(x0,y0),由点Q是线段OP的中点
知x0=2x,y0=2y,又+ =1,所以,即x2+ =1.
(2)由垂直平分线的性质可知|MQ|=|MA|,
∴|CM|+|MA|=|CM|+|MQ|=|CQ|,∴|CM|+|MA|=5.
∴点M的轨迹为椭圆,其中2a=5,焦点为C(-1,0),A(1,0),
∴a=,c=1 ,∴b2=a2-c2=-1= .
∴所求点M的轨迹方程为+=1,即+=1.
【解析】(3)如图,设是点到直线的距离,
根据题意,动点的轨迹就是集合, 由此得,将上式两边平方,并化简,得,即:
5.如图所示,在圆C:(x+1)2+y2=25内有一点A(1,0).Q为圆C上任意一点,线段AQ的垂直平分线与C,Q的连线交于点M,当点Q在圆C上运动时,求点M的轨迹方程.
解:如图所示,连接MA.
由题意知点M在线段CQ上,
从而有|CQ|=|MQ|+|CM|.
又点M在AQ的垂直平分线上,
则|MA|=|MQ|,故|MA|+|MC|=|CQ|=5>|AC|=2.
又A(1,0),C(-1,0),
故点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,
且2a=5,c=1,
课程结束
人教A版数学选择性必修第一册
3.1.1椭圆及其标准方程
1.理解椭圆的定义及椭圆的标准方程.(重点)
2.掌握用定义法和待定系数法求椭圆的标准方程.(重点)
3.理解椭圆标准方程的推导过程,并能运用标准方程解决相关问题.(难点)
椭圆是圆锥曲线的一种具有丰富的几何性质,在科研生产和人类生活中具有广泛的应用,那么椭圆到底有怎样的几何性质,我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础。
取一条定长的细线,把它的两端都固定在图板
的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆。如果把细绳的两端拉开一段距离,分别固定在图板中的两点F1,F2 ,
套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线?在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
常数(大于|F1F2|)
两个定点
两焦点间的距离
一半
观察椭圆的形状,你认为怎样建立坐标系可能使所得的椭圆方程形式简单?
一般地,如果椭圆的焦点为,焦距为2,而且椭圆上的 动点P满足,=2,其中>>0. 以 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示,此时,椭圆的焦点分别为 ,0).
=2. ①
①,我们将其左边一个根式移到右边,得
对方程两边平方,得=
整理,得= ③
对方程③两边平方,得=
整理得 ④
将方程④两边同除以,得 ⑤
由椭圆的定义可知>>0 ,即>>0,所以.
观察图,你能从中找出表示,的线段吗?
由图可知,=,=c
令,那么方程⑤就是
(>>0) ⑥
称⑥式为焦点在轴上的椭圆方程.
设椭圆,焦距为2,而且椭圆上的动点P满足=2其中>>0. 以 所在直线为轴,线段的垂直平分线为轴,建立平面直角坐标系,如图所示,此时:
(1)椭圆焦点的坐标分别是什么?
(2)能否通过 (>>0) 来得到此时椭圆方程的形式?
(>>0),称焦点在轴上的椭圆方程.
2.椭圆的标准方程
焦点在x轴上 焦点在y轴上
标准 方程
图形
焦点坐标 F1(-c,0),F2(c,0) F1(0,-c),F2(0,c)
a,b,c关系 b2=a2-c2
1. a=6,c=1的椭圆的标准方程是( )
A.=1 B.=1 C.=1 D.=1或=1
2. 椭圆+y2=1上一点P到一个焦点的距离为2,则点P到另一个焦点的距离为( )
A.5 B.6 C.7 D.8
3. 椭圆4x2+9y2=1的焦点坐标是( )
A.(±,0) B.(0,±) C. D.
解析: (1) 易得为D选项.
(2)设椭圆的左、右焦点分别为F1,F2,若|PF1|=2,
结合椭圆定义|PF2|+|PF1|=10,可得|PF2|=8.
答案:(1)D (2)D (3)C
例1. 已知 是定点,.若动点满足,则动点的轨迹是( )
直线 B.线段 C.圆 D.椭圆
【答案】B
【解析】对于在平面内,若动点到、两点的距离之和等于6,而6正好等于两定点、的距离,则动点的轨迹是以,为端点的线段.
故选:B.
椭圆是在平面内定义的,所以“平面内”这一条件不能忽视.
定义中到两定点的距离之和是常数,而不能是变量.
常数(2a)必须大于两定点间的距离,否则轨迹不是椭圆,这是判断曲线是否为椭圆的限制条件.
跟踪训练1.若椭圆上一点P到左焦点的距离为5,则其到右焦点的距离为( )
A.5 B.3 C.2 D.1
【答案】D
【解析】由题意a=3,P点到右焦点的距离为2a-5=1.
例2.(1)如果表示焦点在轴上的椭圆,那么实数的取值范围是( )
B.(0,2) C. D.
(2)方程表示椭圆,则实数的取值范围( )
A. B. C. D.且
【答案】(1)A(2)D
【解析】(1)转化为椭圆的标准方程,得,因为表示焦点在轴上的椭圆,所以,解得.所以实数的取值范围是.选A.
(2)方程表示椭圆,若焦点在x轴上,;若焦点在y轴上,.综上:实数的取值范围是且,故选:D
把方程写成椭圆的标准方程形式,得到形式,要想表示
焦点在轴上的椭圆,必须要满足,解这个不等式就可求出实数的取值范围.
焦点在x轴上的椭圆,必须要满足A>B>0,解这个不等式就可求出实数的取值范围.
椭圆,必须要满足解这个不等式就可求出实数的取值范围.
跟踪训练2.“”是“方程表示椭圆”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】B
【解析】因为方程表示椭圆的充要条件是,
即且,故“”是“方程表示椭圆”的必要而不充分条件.故选:B.
例3.(1)已知的顶点,在椭圆上,顶点是椭圆的一个焦点,且椭圆的另一个焦点在上,则的周长是( )
A. B. C. D.
(2)已知是椭圆上一点, 为椭圆的两焦点,且,则面积为( )
A. B. C. D.
【答案】(1)C (2)A
【解析】(1)的顶点,在椭圆上,顶点是椭圆的一个焦点,且椭圆的另一个焦点在上,由椭圆的定义可得:的周长是.故选:C.
(2)由椭圆的标准方程可得:a=5,b=3,∴c=4,
设|PF1|=t1,|PF2|=t2,所以根据椭圆的定义可得:t1+t2=10①,
在△F1PF2中,∠F1PF2=60°,所以根据余弦定理可得:
|PF1|2+|PF2|2﹣2|PF1||PF2|cos60°=|F1F2|2=(2c)2=64,
整理可得:t12+t22﹣t1t2=64,②把①两边平方得t12+t22+2t1 t2=100,③
所以③﹣②得t1t2=12,∴∠F1PF2=3.故选A.
跟踪训练3.已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( )
A.20 B.16 C.18 D.14
【答案】C
【解析】根据椭圆方程可知,根据椭圆的定义可知,的周长为,故选C.
(3)动点到定点的距离和到定直线的距离之比是常数,求动点点的轨迹.
【解】(1)答案x2+=1 解析:设Q(x,y),P(x0,y0),由点Q是线段OP的中点
知x0=2x,y0=2y,又+ =1,所以,即x2+ =1.
(2)由垂直平分线的性质可知|MQ|=|MA|,
∴|CM|+|MA|=|CM|+|MQ|=|CQ|,∴|CM|+|MA|=5.
∴点M的轨迹为椭圆,其中2a=5,焦点为C(-1,0),A(1,0),
∴a=,c=1 ,∴b2=a2-c2=-1= .
∴所求点M的轨迹方程为+=1,即+=1.
【解析】(3)如图,设是点到直线的距离,
根据题意,动点的轨迹就是集合, 由此得,将上式两边平方,并化简,得,即:
5.如图所示,在圆C:(x+1)2+y2=25内有一点A(1,0).Q为圆C上任意一点,线段AQ的垂直平分线与C,Q的连线交于点M,当点Q在圆C上运动时,求点M的轨迹方程.
解:如图所示,连接MA.
由题意知点M在线段CQ上,
从而有|CQ|=|MQ|+|CM|.
又点M在AQ的垂直平分线上,
则|MA|=|MQ|,故|MA|+|MC|=|CQ|=5>|AC|=2.
又A(1,0),C(-1,0),
故点M的轨迹是以(1,0),(-1,0)为焦点的椭圆,
且2a=5,c=1,
课程结束
