11.1.2 三角形的高、中线与角平分线一课一练(含解析)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线一课一练(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 143.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 07:59:02 | ||
图片预览

文档简介
登录二一教育在线组卷平台 助您教考全无忧
11.1.2 三角形的高、中线与角平分线一课一练
一、单选题
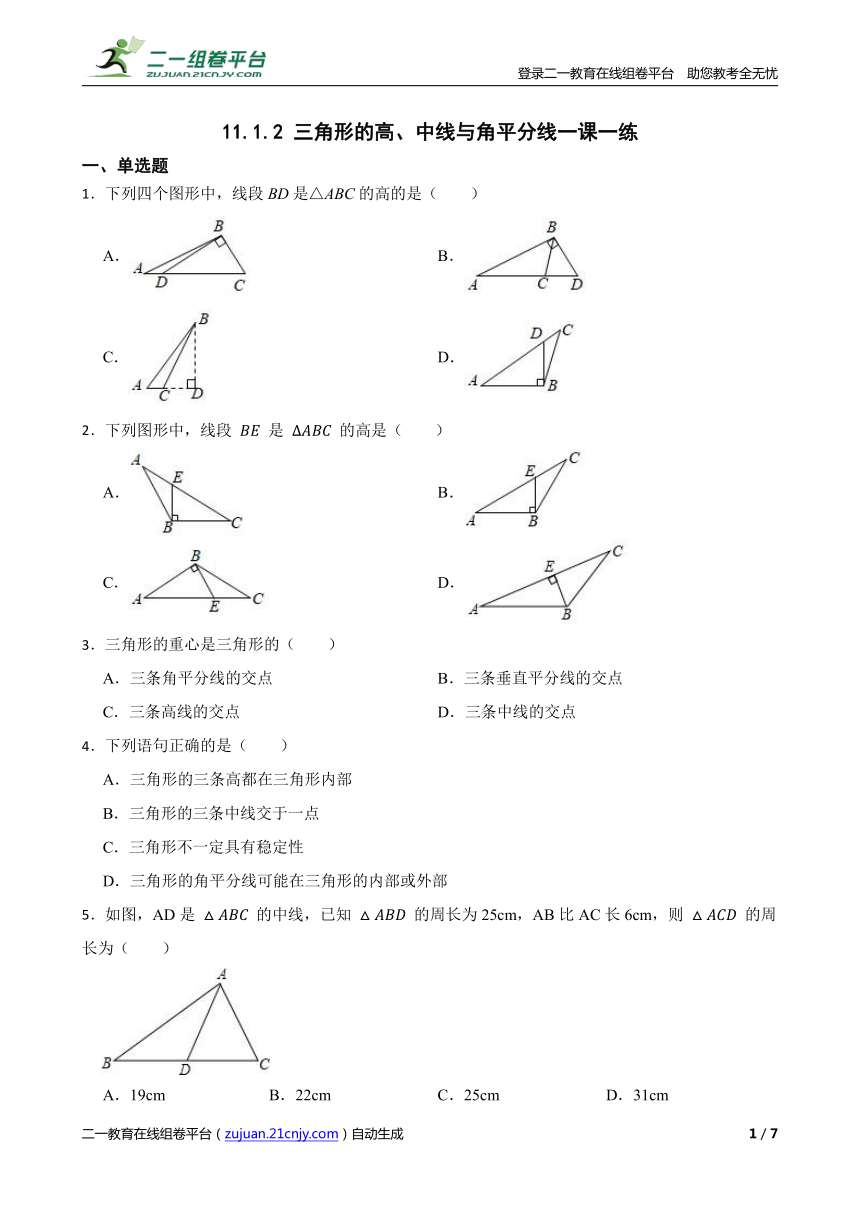
1.下列四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
2.下列图形中,线段 是 的高是( )
A. B.
C. D.
3.三角形的重心是三角形的( )
A.三条角平分线的交点 B.三条垂直平分线的交点
C.三条高线的交点 D.三条中线的交点
4.下列语句正确的是( )
A.三角形的三条高都在三角形内部
B.三角形的三条中线交于一点
C.三角形不一定具有稳定性
D.三角形的角平分线可能在三角形的内部或外部
5.如图,AD是 的中线,已知 的周长为25cm,AB比AC长6cm,则 的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
6.如图,在中,已知点D、点E分别为BC、AD的中点,且的面积为3,则的面积是 .
三、计算题
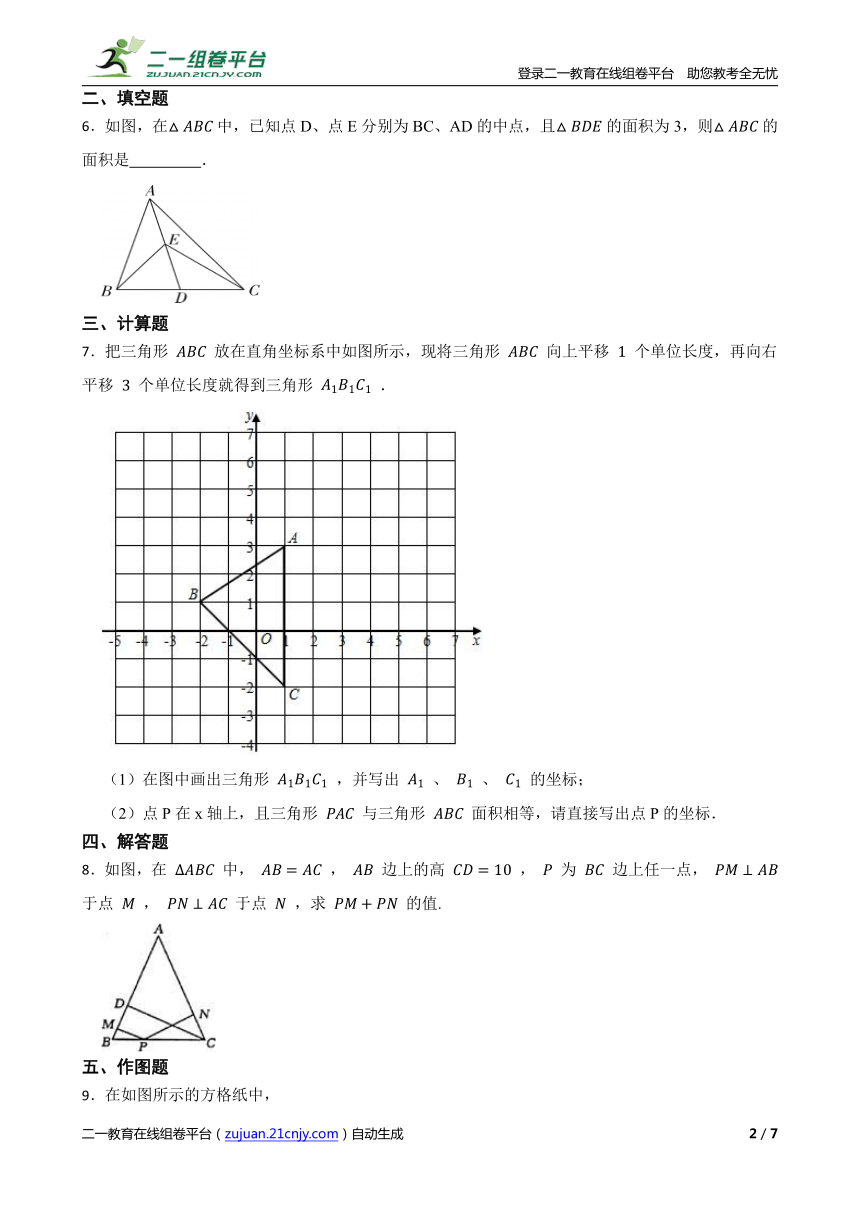
7.把三角形 放在直角坐标系中如图所示,现将三角形 向上平移 个单位长度,再向右平移 个单位长度就得到三角形 .
(1)在图中画出三角形 ,并写出 、 、 的坐标;
(2)点P在x轴上,且三角形 与三角形 面积相等,请直接写出点P的坐标.
四、解答题
8.如图,在 中, , 边上的高 , 为 边上任一点, 于点 , 于点 ,求 的值.
五、作图题
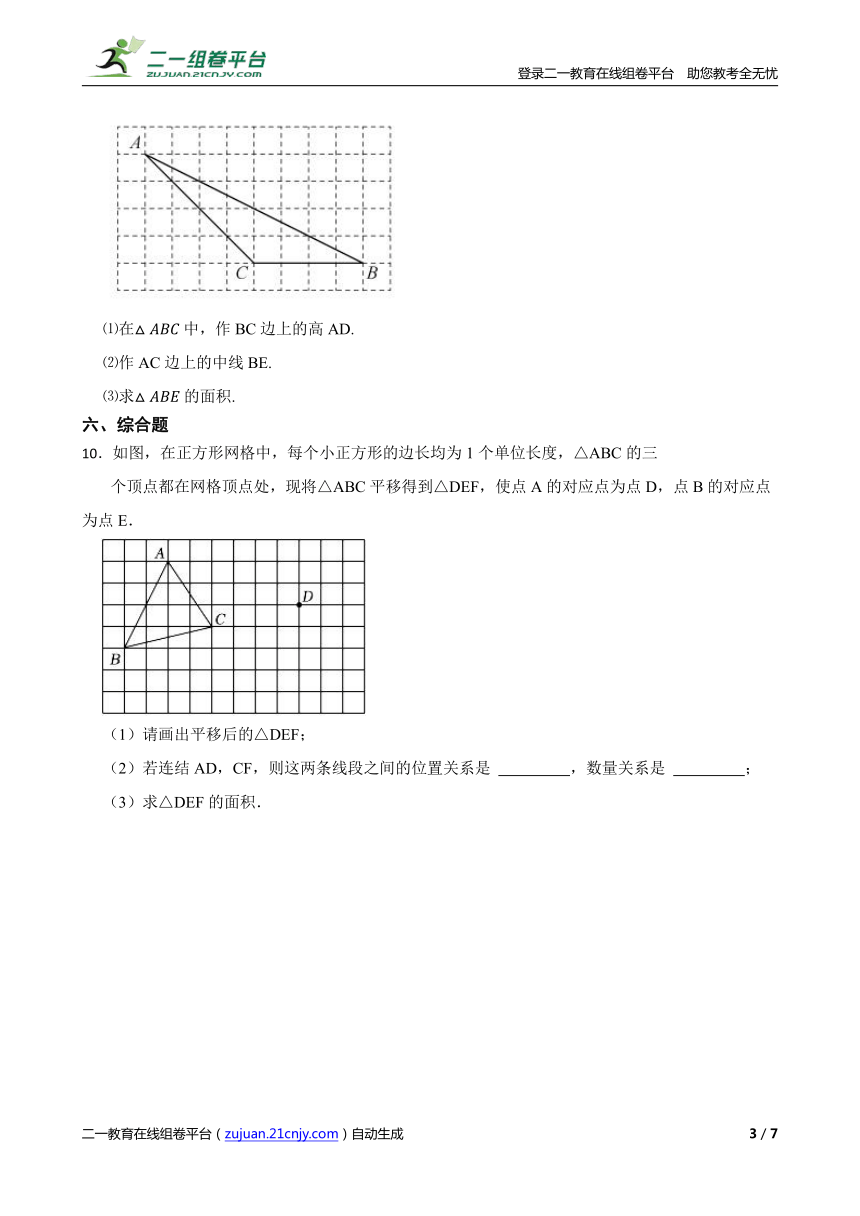
9.在如图所示的方格纸中,
⑴在中,作BC边上的高AD.
⑵作AC边上的中线BE.
⑶求的面积.
六、综合题
10.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三
个顶点都在网格顶点处,现将△ABC平移得到△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)请画出平移后的△DEF;
(2)若连结AD,CF,则这两条线段之间的位置关系是 ,数量关系是 ;
(3)求△DEF的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:A、线段BD是 的高,选项不符合题意;
B、线段BD是 的高,选项不符合题意;
C、线段BD是 的高,选项符合题意;
D、线段BD是 的高,选项不符合题意.
故答案为:C
【分析】利用高的定义对每个图形一一判断即可。
2.【答案】D
【解析】【解答】在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高.
故答案为:D
【分析】根据三角形高的定义可得结论
3.【答案】D
【解析】【解答】A、三角形的三条角平分线的交点是三角形的内心,此项不符题意;
B、三角形的三条垂直平分线的交点是三角形的外心,此项不符题意;
C、三角形的三条高线的交点是三角形的垂心,此项不符题意;
D、三角形的三条中线的交点是三角形的重心,此项符合题意;
故答案为:D.
【分析】根据三角形的重心的含义,即可得到答案。
4.【答案】B
【解析】【解答】解:A、三角形的三条高不一定在三角形内部,错误;
B、三角形的三条中线交于一点,正确;
C、三角形具有稳定性,错误;
D、三角形的角平分线一定在三角形的内部,错误;
故选B
【分析】根据三角形的角平分线、高和中线的定义判断即可.
5.【答案】A
【解析】【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长6cm,
∴△ACD周长为:25﹣6=19cm.
故答案为:A.
【分析】由三角形中线的概念可得BD=CD,又AD是△ABD和△ACD的公共边,故△ABD和△ACD周长的差=AB﹣AC=6,已知 的周长为25cm,故可求得 的周长.
6.【答案】12
【解析】【解答】解:点是的中点, 的面积为3,
,
点是的中点,
,,
,
故答案为:12.
【分析】利用中线的性质求得各小三角形的面积,再计算的面积.
7.【答案】(1)解:如图所示:
、 、 、 ;
(2) ,
【解析】【解答】解:(2)∵S△ABC= = ,
∴S△PAC= ,
∵AC=5,
∴点P到AC的距离为 =3,
∴点P的坐标 , .
【分析】(1)根据点坐标平移的性质得到A1、B1、C1,再连接作出三角形,并直接写出点的坐标即可;
(2)根据三角形的面积公式可得三角形的面积,然后再确定P点坐标即可。
8.【答案】解:连接 ,
∵CD⊥AB, , ,
∴ , , ,
∵ ,
∴ ,
又∵ , ,
∴ .
【解析】【分析】连接AP,根据三角形面积的计算公式即可得到PM+PN的值。
9.【答案】解:⑴如图所示AD即为所求.
⑵如图所示BE即为所求.
⑶,,
,
为边上中线,
,
即面积为4.
【解析】【分析】(1)根据垂线的作法进行作图;
(2)找出线段AC的中点E,然后连接BE即可;
(3)根据中线的概念结合三角形的面积公式可得S△ABE=S△ABC,据此计算.
10.【答案】(1)解:如图所示,△DEF即为所求;
(2)平行;相等
(3)解:S△DEF=4×4﹣ ×2×3﹣ ×4×2﹣ ×1×4=7
【解析】【解答】解:(2)∵△DEF是由△ABC平移得到的,
∴AD∥CF,AD=CF.
【分析】(1)根据点A、D的位置可得平移步骤为:先向右平移6格,再向下平移2格,据此找出点E、F的位置,然后顺次连接即可;
(2)根据平移的性质进行解答;
(3)利用方格纸的特点及割补法,用△DEF外接矩形的面积分别减去周围三个三角形的面积,即可求出△DEF的面积.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
11.1.2 三角形的高、中线与角平分线一课一练
一、单选题
1.下列四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
2.下列图形中,线段 是 的高是( )
A. B.
C. D.
3.三角形的重心是三角形的( )
A.三条角平分线的交点 B.三条垂直平分线的交点
C.三条高线的交点 D.三条中线的交点
4.下列语句正确的是( )
A.三角形的三条高都在三角形内部
B.三角形的三条中线交于一点
C.三角形不一定具有稳定性
D.三角形的角平分线可能在三角形的内部或外部
5.如图,AD是 的中线,已知 的周长为25cm,AB比AC长6cm,则 的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
6.如图,在中,已知点D、点E分别为BC、AD的中点,且的面积为3,则的面积是 .
三、计算题
7.把三角形 放在直角坐标系中如图所示,现将三角形 向上平移 个单位长度,再向右平移 个单位长度就得到三角形 .
(1)在图中画出三角形 ,并写出 、 、 的坐标;
(2)点P在x轴上,且三角形 与三角形 面积相等,请直接写出点P的坐标.
四、解答题
8.如图,在 中, , 边上的高 , 为 边上任一点, 于点 , 于点 ,求 的值.
五、作图题
9.在如图所示的方格纸中,
⑴在中,作BC边上的高AD.
⑵作AC边上的中线BE.
⑶求的面积.
六、综合题
10.如图,在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三
个顶点都在网格顶点处,现将△ABC平移得到△DEF,使点A的对应点为点D,点B的对应点为点E.
(1)请画出平移后的△DEF;
(2)若连结AD,CF,则这两条线段之间的位置关系是 ,数量关系是 ;
(3)求△DEF的面积.
答案解析部分
1.【答案】C
【解析】【解答】解:A、线段BD是 的高,选项不符合题意;
B、线段BD是 的高,选项不符合题意;
C、线段BD是 的高,选项符合题意;
D、线段BD是 的高,选项不符合题意.
故答案为:C
【分析】利用高的定义对每个图形一一判断即可。
2.【答案】D
【解析】【解答】在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高.
故答案为:D
【分析】根据三角形高的定义可得结论
3.【答案】D
【解析】【解答】A、三角形的三条角平分线的交点是三角形的内心,此项不符题意;
B、三角形的三条垂直平分线的交点是三角形的外心,此项不符题意;
C、三角形的三条高线的交点是三角形的垂心,此项不符题意;
D、三角形的三条中线的交点是三角形的重心,此项符合题意;
故答案为:D.
【分析】根据三角形的重心的含义,即可得到答案。
4.【答案】B
【解析】【解答】解:A、三角形的三条高不一定在三角形内部,错误;
B、三角形的三条中线交于一点,正确;
C、三角形具有稳定性,错误;
D、三角形的角平分线一定在三角形的内部,错误;
故选B
【分析】根据三角形的角平分线、高和中线的定义判断即可.
5.【答案】A
【解析】【解答】解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)﹣(AC+AD+CD)=AB﹣AC,
∵△ABD的周长为25cm,AB比AC长6cm,
∴△ACD周长为:25﹣6=19cm.
故答案为:A.
【分析】由三角形中线的概念可得BD=CD,又AD是△ABD和△ACD的公共边,故△ABD和△ACD周长的差=AB﹣AC=6,已知 的周长为25cm,故可求得 的周长.
6.【答案】12
【解析】【解答】解:点是的中点, 的面积为3,
,
点是的中点,
,,
,
故答案为:12.
【分析】利用中线的性质求得各小三角形的面积,再计算的面积.
7.【答案】(1)解:如图所示:
、 、 、 ;
(2) ,
【解析】【解答】解:(2)∵S△ABC= = ,
∴S△PAC= ,
∵AC=5,
∴点P到AC的距离为 =3,
∴点P的坐标 , .
【分析】(1)根据点坐标平移的性质得到A1、B1、C1,再连接作出三角形,并直接写出点的坐标即可;
(2)根据三角形的面积公式可得三角形的面积,然后再确定P点坐标即可。
8.【答案】解:连接 ,
∵CD⊥AB, , ,
∴ , , ,
∵ ,
∴ ,
又∵ , ,
∴ .
【解析】【分析】连接AP,根据三角形面积的计算公式即可得到PM+PN的值。
9.【答案】解:⑴如图所示AD即为所求.
⑵如图所示BE即为所求.
⑶,,
,
为边上中线,
,
即面积为4.
【解析】【分析】(1)根据垂线的作法进行作图;
(2)找出线段AC的中点E,然后连接BE即可;
(3)根据中线的概念结合三角形的面积公式可得S△ABE=S△ABC,据此计算.
10.【答案】(1)解:如图所示,△DEF即为所求;
(2)平行;相等
(3)解:S△DEF=4×4﹣ ×2×3﹣ ×4×2﹣ ×1×4=7
【解析】【解答】解:(2)∵△DEF是由△ABC平移得到的,
∴AD∥CF,AD=CF.
【分析】(1)根据点A、D的位置可得平移步骤为:先向右平移6格,再向下平移2格,据此找出点E、F的位置,然后顺次连接即可;
(2)根据平移的性质进行解答;
(3)利用方格纸的特点及割补法,用△DEF外接矩形的面积分别减去周围三个三角形的面积,即可求出△DEF的面积.
二一教育在线组卷平台(zujuan.21cnjy.com)自动生成 1 / 1
