5.1.1 相交线课时卷
文档属性
| 名称 | 5.1.1 相交线课时卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 108.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-12 12:01:08 | ||
图片预览


文档简介
八年级数学(下)课时卷
5.1.1 相交线
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
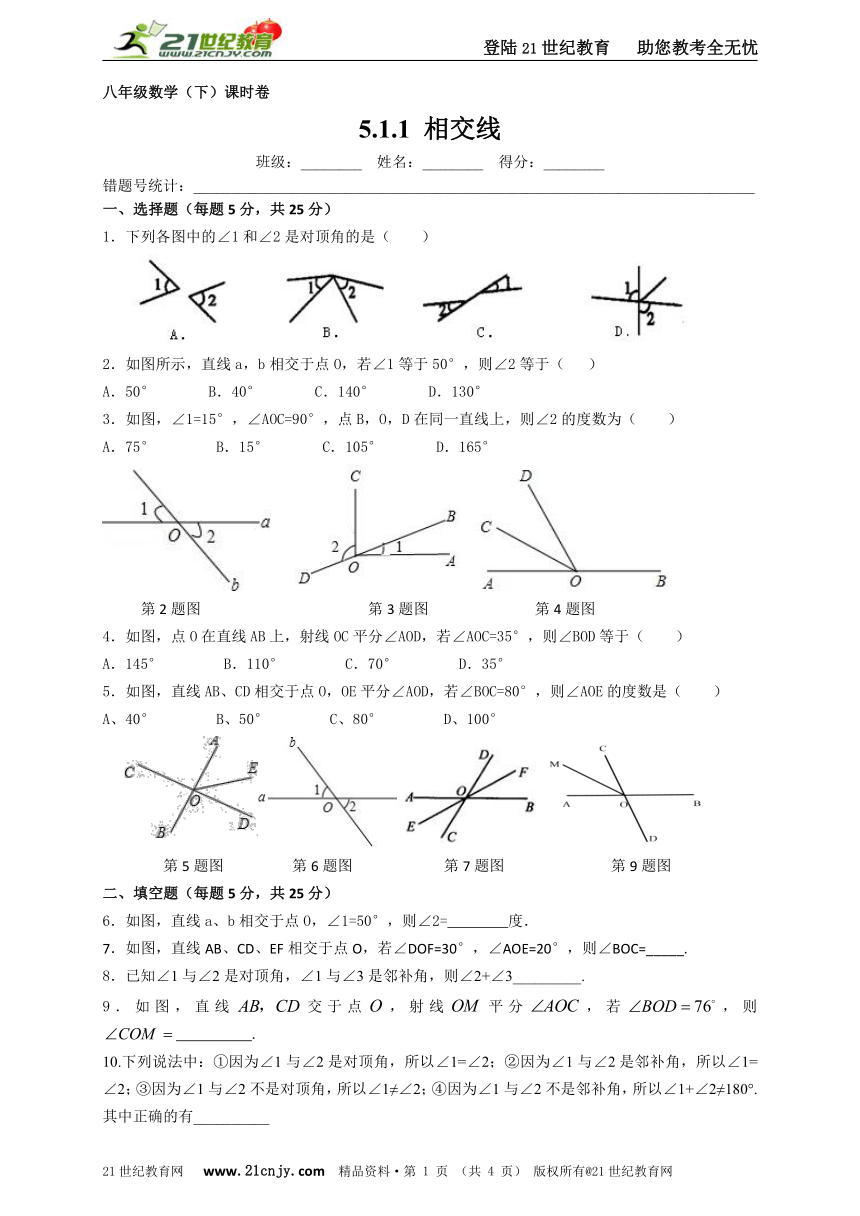
1.下列各图中的∠1和∠2是对顶角的是( )
2.如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50° B.40° C.140° D.130°
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
第2题图 第3题图 第4题图
4.如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD等于( )
A.145° B.110° C.70° D.35°
5.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( )
A、40° B、50° C、80° D、100°
第5题图 第6题图 第7题图 第9题图
二、填空题(每题5分,共25分)
6.如图,直线a、b相交于点O,∠1=50°,则∠2= 度.
7.如图,直线AB、CD、EF相交于点O,若∠DOF=30°,∠AOE=20°,则∠BOC=_____.
8.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3_________.
9.如图,直线交于点,射线平分,若,则 .
10.下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
其中正确的有__________
三、解答题(共50分)
11.(10分)如图所示,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=2∠AOC,求∠DOF.
12.(10分)∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
13.(15分)如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.21教育网
14.(15分)数一数,两条直线相交于一点,共有__________对对顶角;三条直线相交于一点,共有__________对对顶角;四条直线相交于一点,共有__________对对顶角;….
(1)找规律:n条直线相交于一点,共有__________对对顶角;
(2)利用规律计算100条直线相交于一点,共有多少对对顶角.
参考答案
5.1.1 相交线
3.C.
【解析】∵∠1=15°,∠AOC=90°,
∴∠BOC=75°,
∵∠2+∠BOC=180°,
∴∠2=105°.
故选C.
4.B.
【解析】∵射线OC平分∠DOA.
∴∠AOD=2∠AOC,
∵∠COA=35°,
∴∠DOA=70°,
∴∠BOD=180°﹣70°=110°,
故选:B.
5.A
【解析】根据角平分线的定义计算.
∵∠BOC=80°,
∴∠AOD=∠BOC=80度.
∵OE平分∠AOD,
∴∠AOE=∠AOD=×80°=40度.
故选A.
6.50.
【解析】直接根据对顶角相等即可求解:
∵直线a、b相交于点O,∴∠2与∠1是对顶角.
∵∠1=50°,∴∠2=∠1=50°.
7.130°.
【解析】根据平角定义和∠DOF=30°,∠AOE=20°先求出∠AOD的度数,再根据对顶角相等即可求出∠BOC的度数.21世纪教育网版权所有
试题解析:∵∠DOF=30°,∠AOE=20°,
∴∠AOD=180°-∠DOF-∠AOE=180°-30°-20°=130°,
∴∠BOC=∠AOD=130°.
8.180°
【解析】根据邻补角定义可知,∠1+∠3=180°,由对顶角的性质:对顶角相等可得∠1=∠2,所以∠2+∠3=180°(等量代换)21cnjy.com
9.380.
【解析】根据对顶角相等,和平分线的定义可得.
10. ①
【解析】①满足对顶角的性质,所以正确,②邻补角是特殊位置的补角,由互补的性质可知其和应180°,而不是∠1=∠2,所以不正确;③中的∠1与∠2不是对顶角是从位置上看的,但它们在数量上是可以相等,所以也不正确;④的原因同③. 所以本题填①.www.21-cn-jy.com
11.20°.
【解析】 图形中∠BOC与∠AOC互为邻补角,结合已知条件:∠BOC=2∠AOC,则可求出∠AOC,要求∠DOF只需求它的对顶角∠EOC即可,本题可用方程求解2·1·c·n·j·y
解:设∠AOC=x°,则∠BOC=(2x)°.
因为∠AOC与∠BOC是邻补角,所以∠AOC+∠BOC=180°
所以x+2x=180
解得x=60
所以∠AOC=60°.因为∠DOF与∠EOC是对顶角,
所以∠DOF=∠EOC=∠AOC-∠AOE=60°-40°=20°
12.∠3=54°,∠4=72°.
【解析】本题首先根据方程思想,求出. ∠1、∠2的度数,再根据对顶角、邻补角的关系求出∠3与∠4的度数.21·世纪*教育网
解:由已知∠1=∠2,∠1+∠2=162°,
解得:∠1=54°,∠2=108°.
∵∠1与∠3是对顶角,
∴∠3=∠1=54°.
∵∠2与∠4是邻补角,
∴∠4=180°﹣∠2=72°.?
13.∠3 =52.5°.
【解析】根据对顶角的性质,∠1=∠BOF,∠2=∠AOC,从而得出∠COF=105°,再根据OG平分∠COF,可得∠3的度数.【来源:21·世纪·教育·网】
解:∵∠1=30°,∠2=45°
∴∠EOD=180°﹣∠1﹣∠2=105°
∴∠COF=∠EOD=105°
又∵OG平分∠COF,
∴∠3=∠COF=52.5°.
14.2,6,12;(1)n(n-1);(2)9900
【解析】如图所示,两条直线相交于一点,共有2对对顶角;三条直线相交于一点,共有6对对顶角;四条直线相交于一点,共有12对对顶角.21·cn·jy·com
5.1.1 相交线
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.下列各图中的∠1和∠2是对顶角的是( )
2.如图所示,直线a,b相交于点O,若∠1等于50°,则∠2等于( )
A.50° B.40° C.140° D.130°
3.如图,∠1=15°,∠AOC=90°,点B,O,D在同一直线上,则∠2的度数为( )
A.75° B.15° C.105° D.165°
第2题图 第3题图 第4题图
4.如图,点O在直线AB上,射线OC平分∠AOD,若∠AOC=35°,则∠BOD等于( )
A.145° B.110° C.70° D.35°
5.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是( )
A、40° B、50° C、80° D、100°
第5题图 第6题图 第7题图 第9题图
二、填空题(每题5分,共25分)
6.如图,直线a、b相交于点O,∠1=50°,则∠2= 度.
7.如图,直线AB、CD、EF相交于点O,若∠DOF=30°,∠AOE=20°,则∠BOC=_____.
8.已知∠1与∠2是对顶角,∠1与∠3是邻补角,则∠2+∠3_________.
9.如图,直线交于点,射线平分,若,则 .
10.下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
其中正确的有__________
三、解答题(共50分)
11.(10分)如图所示,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=2∠AOC,求∠DOF.
12.(10分)∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.
13.(15分)如图,直线AB、CD、EF相交于点O,OG平分∠COF,∠1=30°,∠2=45°.求∠3的度数.21教育网
14.(15分)数一数,两条直线相交于一点,共有__________对对顶角;三条直线相交于一点,共有__________对对顶角;四条直线相交于一点,共有__________对对顶角;….
(1)找规律:n条直线相交于一点,共有__________对对顶角;
(2)利用规律计算100条直线相交于一点,共有多少对对顶角.
参考答案
5.1.1 相交线
3.C.
【解析】∵∠1=15°,∠AOC=90°,
∴∠BOC=75°,
∵∠2+∠BOC=180°,
∴∠2=105°.
故选C.
4.B.
【解析】∵射线OC平分∠DOA.
∴∠AOD=2∠AOC,
∵∠COA=35°,
∴∠DOA=70°,
∴∠BOD=180°﹣70°=110°,
故选:B.
5.A
【解析】根据角平分线的定义计算.
∵∠BOC=80°,
∴∠AOD=∠BOC=80度.
∵OE平分∠AOD,
∴∠AOE=∠AOD=×80°=40度.
故选A.
6.50.
【解析】直接根据对顶角相等即可求解:
∵直线a、b相交于点O,∴∠2与∠1是对顶角.
∵∠1=50°,∴∠2=∠1=50°.
7.130°.
【解析】根据平角定义和∠DOF=30°,∠AOE=20°先求出∠AOD的度数,再根据对顶角相等即可求出∠BOC的度数.21世纪教育网版权所有
试题解析:∵∠DOF=30°,∠AOE=20°,
∴∠AOD=180°-∠DOF-∠AOE=180°-30°-20°=130°,
∴∠BOC=∠AOD=130°.
8.180°
【解析】根据邻补角定义可知,∠1+∠3=180°,由对顶角的性质:对顶角相等可得∠1=∠2,所以∠2+∠3=180°(等量代换)21cnjy.com
9.380.
【解析】根据对顶角相等,和平分线的定义可得.
10. ①
【解析】①满足对顶角的性质,所以正确,②邻补角是特殊位置的补角,由互补的性质可知其和应180°,而不是∠1=∠2,所以不正确;③中的∠1与∠2不是对顶角是从位置上看的,但它们在数量上是可以相等,所以也不正确;④的原因同③. 所以本题填①.www.21-cn-jy.com
11.20°.
【解析】 图形中∠BOC与∠AOC互为邻补角,结合已知条件:∠BOC=2∠AOC,则可求出∠AOC,要求∠DOF只需求它的对顶角∠EOC即可,本题可用方程求解2·1·c·n·j·y
解:设∠AOC=x°,则∠BOC=(2x)°.
因为∠AOC与∠BOC是邻补角,所以∠AOC+∠BOC=180°
所以x+2x=180
解得x=60
所以∠AOC=60°.因为∠DOF与∠EOC是对顶角,
所以∠DOF=∠EOC=∠AOC-∠AOE=60°-40°=20°
12.∠3=54°,∠4=72°.
【解析】本题首先根据方程思想,求出. ∠1、∠2的度数,再根据对顶角、邻补角的关系求出∠3与∠4的度数.21·世纪*教育网
解:由已知∠1=∠2,∠1+∠2=162°,
解得:∠1=54°,∠2=108°.
∵∠1与∠3是对顶角,
∴∠3=∠1=54°.
∵∠2与∠4是邻补角,
∴∠4=180°﹣∠2=72°.?
13.∠3 =52.5°.
【解析】根据对顶角的性质,∠1=∠BOF,∠2=∠AOC,从而得出∠COF=105°,再根据OG平分∠COF,可得∠3的度数.【来源:21·世纪·教育·网】
解:∵∠1=30°,∠2=45°
∴∠EOD=180°﹣∠1﹣∠2=105°
∴∠COF=∠EOD=105°
又∵OG平分∠COF,
∴∠3=∠COF=52.5°.
14.2,6,12;(1)n(n-1);(2)9900
【解析】如图所示,两条直线相交于一点,共有2对对顶角;三条直线相交于一点,共有6对对顶角;四条直线相交于一点,共有12对对顶角.21·cn·jy·com
