5.1.2 垂线课时卷
图片预览

文档简介
八年级数学(下)课时卷
5.1.2 垂线
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.下面说法中错误的是( )
A.两条直线相交,有一个角是直角,则这两条直线互相垂直
B.若两对顶角之和为1800,则两条直线互相垂直
C.两条直线相交,所构成的四个角中,若有两个角相等,则两条直线互相垂直
D.两条直线相交,所构成的四个角中,若有三个角相等,则两条直线互相垂直
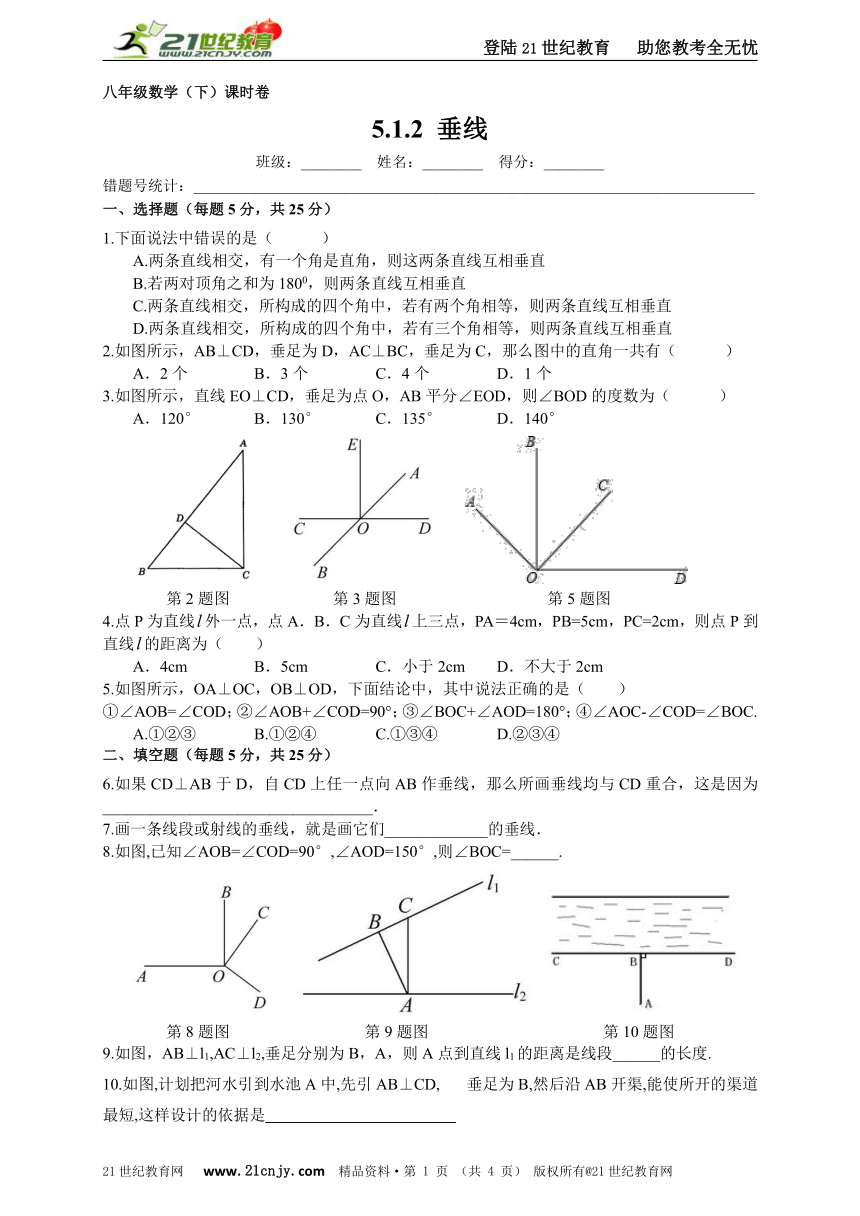
2.如图所示,AB⊥CD,垂足为D,AC⊥BC,垂足为C,那么图中的直角一共有( )
A.2个 B.3个 C.4个 D.1个
3.如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
第2题图 第3题图 第5题图
4.点P为直线外一点,点A.B.C为直线上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线的距离为( ) 21cnjy.com
A.4cm B.5cm C.小于2cm D.不大于2cm
5.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每题5分,共25分)
6.如果CD⊥AB于D,自CD上任一点向AB作垂线,那么所画垂线均与CD重合,这是因为__________________________________.【来源:21·世纪·教育·网】
7.画一条线段或射线的垂线,就是画它们_____________的垂线.
8.如图,已知∠AOB=∠COD=90°,∠AOD=150°,则∠BOC=______.
第8题图 第9题图 第10题图
9.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段______的长度.
10.如图,计划把河水引到水池A中,先引AB⊥CD, 垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 21·世纪*教育网
三、解答题(共50分)
11.如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.www-2-1-cnjy-com
12.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
13.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①____________;②____________.
(2)如果∠AOD= 400,则①∠BOC=_______;②OP是∠BOC的平分线,所以∠COP=______度;
③求∠BOF的度数.
14.如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
参考答案
5.1.2 垂线
一、选择题
2、B
【解析】根据垂直定义即可判断∠ADC=90°,∠BDC=90°,∠ACB=90°,
3、C.
【解析】根据垂直的定义,直线EO⊥CD,所以∠EOD=90°,再由角平分线的定义得∠AOD=45°,所以∠BOD=180°-45°=135°21世纪教育网版权所有
4、D
【解析】点P到直线l的距离为点P到直线l的垂线段,结合已知,因此点P到直线l的距离小于等于2.
解:∵根据点到直线的距离为点到直线的垂线段(垂线段最短),
2<4<5,
∴点P到直线l的距离小于等于2,即不大于2,
故选:D.
5、C
【解析】本题考查了余角和补角,垂直的定义,是基础题,根据垂直的定义和同角的余角
相等分别计算,然后对各小题分析判断即可得解.
解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠AOB+∠COD不一定等于90°,故②错误;
∠BOC+∠AOD=90°-∠AOB+90°+∠AOB=180°,故③正确;
∠AOC-∠COD=∠AOC-∠AOB=∠BOC,故④正确;
综上所述,说法正确的是①③④.
故选C.
二、填空题
6、过一点有且只有一条直线与已知直线垂直
7、所在直线
8、30°
【解析】∠BOC=360°-∠AOB-∠COD-∠AOD=360°-90°-90°-150°=30°.
9、AB
【解析】因为AB⊥l1,由点到直线的距离可知,A点到直线l1的距离是线段AB的长度.
10、垂线段最短
【解析】垂线段最短在实际生活中有着广泛的用途
三、解答题
11、相等.
【解析】
因为∠AOB+∠DOE=90°,所以∠BOD=180°-(∠AOB+∠DOE)=
180°-90°=90°,又因为OB平分∠AOC,所以∠AOB=∠BOC,又∠AOB+∠DOE=
90°,∠BOC+∠COD=90°,由等角的余角相等,可得∠COD与∠DOE相等.
12、∠2=600 ∠3=30°
【解析】
解:由题意得:
∠3=∠1=30°(对顶角相等)
∵AB⊥CD(已知)
∴∠BOD=900(垂直的定义)
∴∠3+∠2=900
即30°+∠2=900
∴∠2=600
13、(1)①∠POC=∠POB;②∠EOC=∠FOB.
(2)①∠BOC=400;②∠POC=200.③∠BOF=500
【解析】(1)①由角平分线的定义可知∠POC=∠POB;②由等角的余角相等可得∠EOC=∠FOB.(2)①∵∠AOD=∠BOC,∴∠BOC=∠AOD=400;②∵OP是∠BOC的平分线∴∠POC=∠BOC=200.③∵OF⊥CD,∴∠DOF=900∴∠BOF=∠AOB -∠AOD -∠DOF=500
14、(1)45°;(2)∠EOF=∠AOB;(3)52°.
【解析】(1)先求出∠AOC的度数,再根据角平分线的定义求出∠EOC与∠COF的度数,然后相减即可得解;21教育网
(2)设∠COF=x,∠EOB=y,先用x,y表示出∠EOF,再用x,y表示出∠AOB,然后得出两者的关系;21·cn·jy·com
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
解:(1)∵∠AOB是直角,∠BOC=60°,∴∠AOC=∠AOB+∠BOC=90°+60°=150°,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=∠AOC=×150°=75°,∠COF=∠BOC=×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;www.21-cn-jy.com
(2)设∠COF=x,∠EOB=y,∵OE平分∠AOC,OF平分∠BOC,∴∠BOF= x,∠AOE=∠EOC=2x+y,∴∠EOF=x+y,∠AOB=2x+2y,∴∠EOF=∠AOB;2·1·c·n·j·y
5.1.2 垂线
班级:________ 姓名:________ 得分:________
错题号统计:__________________________________________________________________________
一、选择题(每题5分,共25分)
1.下面说法中错误的是( )
A.两条直线相交,有一个角是直角,则这两条直线互相垂直
B.若两对顶角之和为1800,则两条直线互相垂直
C.两条直线相交,所构成的四个角中,若有两个角相等,则两条直线互相垂直
D.两条直线相交,所构成的四个角中,若有三个角相等,则两条直线互相垂直
2.如图所示,AB⊥CD,垂足为D,AC⊥BC,垂足为C,那么图中的直角一共有( )
A.2个 B.3个 C.4个 D.1个
3.如图所示,直线EO⊥CD,垂足为点O,AB平分∠EOD,则∠BOD的度数为( )
A.120° B.130° C.135° D.140°
第2题图 第3题图 第5题图
4.点P为直线外一点,点A.B.C为直线上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线的距离为( ) 21cnjy.com
A.4cm B.5cm C.小于2cm D.不大于2cm
5.如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(每题5分,共25分)
6.如果CD⊥AB于D,自CD上任一点向AB作垂线,那么所画垂线均与CD重合,这是因为__________________________________.【来源:21·世纪·教育·网】
7.画一条线段或射线的垂线,就是画它们_____________的垂线.
8.如图,已知∠AOB=∠COD=90°,∠AOD=150°,则∠BOC=______.
第8题图 第9题图 第10题图
9.如图,AB⊥l1,AC⊥l2,垂足分别为B,A,则A点到直线l1的距离是线段______的长度.
10.如图,计划把河水引到水池A中,先引AB⊥CD, 垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是 21·世纪*教育网
三、解答题(共50分)
11.如图,已知A,O,E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.www-2-1-cnjy-com
12.如图,∠1=30°,AB⊥CD,垂足为O,EF经过点O.求∠2、∠3的度数.
13.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD,
(1)图中除直角外,还有相等的角吗?请写出两对:①____________;②____________.
(2)如果∠AOD= 400,则①∠BOC=_______;②OP是∠BOC的平分线,所以∠COP=______度;
③求∠BOF的度数.
14.如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
参考答案
5.1.2 垂线
一、选择题
2、B
【解析】根据垂直定义即可判断∠ADC=90°,∠BDC=90°,∠ACB=90°,
3、C.
【解析】根据垂直的定义,直线EO⊥CD,所以∠EOD=90°,再由角平分线的定义得∠AOD=45°,所以∠BOD=180°-45°=135°21世纪教育网版权所有
4、D
【解析】点P到直线l的距离为点P到直线l的垂线段,结合已知,因此点P到直线l的距离小于等于2.
解:∵根据点到直线的距离为点到直线的垂线段(垂线段最短),
2<4<5,
∴点P到直线l的距离小于等于2,即不大于2,
故选:D.
5、C
【解析】本题考查了余角和补角,垂直的定义,是基础题,根据垂直的定义和同角的余角
相等分别计算,然后对各小题分析判断即可得解.
解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠AOB+∠COD不一定等于90°,故②错误;
∠BOC+∠AOD=90°-∠AOB+90°+∠AOB=180°,故③正确;
∠AOC-∠COD=∠AOC-∠AOB=∠BOC,故④正确;
综上所述,说法正确的是①③④.
故选C.
二、填空题
6、过一点有且只有一条直线与已知直线垂直
7、所在直线
8、30°
【解析】∠BOC=360°-∠AOB-∠COD-∠AOD=360°-90°-90°-150°=30°.
9、AB
【解析】因为AB⊥l1,由点到直线的距离可知,A点到直线l1的距离是线段AB的长度.
10、垂线段最短
【解析】垂线段最短在实际生活中有着广泛的用途
三、解答题
11、相等.
【解析】
因为∠AOB+∠DOE=90°,所以∠BOD=180°-(∠AOB+∠DOE)=
180°-90°=90°,又因为OB平分∠AOC,所以∠AOB=∠BOC,又∠AOB+∠DOE=
90°,∠BOC+∠COD=90°,由等角的余角相等,可得∠COD与∠DOE相等.
12、∠2=600 ∠3=30°
【解析】
解:由题意得:
∠3=∠1=30°(对顶角相等)
∵AB⊥CD(已知)
∴∠BOD=900(垂直的定义)
∴∠3+∠2=900
即30°+∠2=900
∴∠2=600
13、(1)①∠POC=∠POB;②∠EOC=∠FOB.
(2)①∠BOC=400;②∠POC=200.③∠BOF=500
【解析】(1)①由角平分线的定义可知∠POC=∠POB;②由等角的余角相等可得∠EOC=∠FOB.(2)①∵∠AOD=∠BOC,∴∠BOC=∠AOD=400;②∵OP是∠BOC的平分线∴∠POC=∠BOC=200.③∵OF⊥CD,∴∠DOF=900∴∠BOF=∠AOB -∠AOD -∠DOF=500
14、(1)45°;(2)∠EOF=∠AOB;(3)52°.
【解析】(1)先求出∠AOC的度数,再根据角平分线的定义求出∠EOC与∠COF的度数,然后相减即可得解;21教育网
(2)设∠COF=x,∠EOB=y,先用x,y表示出∠EOF,再用x,y表示出∠AOB,然后得出两者的关系;21·cn·jy·com
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
解:(1)∵∠AOB是直角,∠BOC=60°,∴∠AOC=∠AOB+∠BOC=90°+60°=150°,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=∠AOC=×150°=75°,∠COF=∠BOC=×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;www.21-cn-jy.com
(2)设∠COF=x,∠EOB=y,∵OE平分∠AOC,OF平分∠BOC,∴∠BOF= x,∠AOE=∠EOC=2x+y,∴∠EOF=x+y,∠AOB=2x+2y,∴∠EOF=∠AOB;2·1·c·n·j·y
