第22章二次函数单元复习课件
文档属性
| 名称 | 第22章二次函数单元复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-12 11:05:39 | ||
图片预览





文档简介
课件20张PPT。 二次函数复习(1)严红然
河北保定市满城县满城镇中学题组一 梳理知识,关注数学思想方法1、下列函数中,是二次函数的是 .
① ② ③
④ ⑤ ⑥
⑦ ⑧
2.当m_______时,函数y=(m+1)χ - 2χ+1是
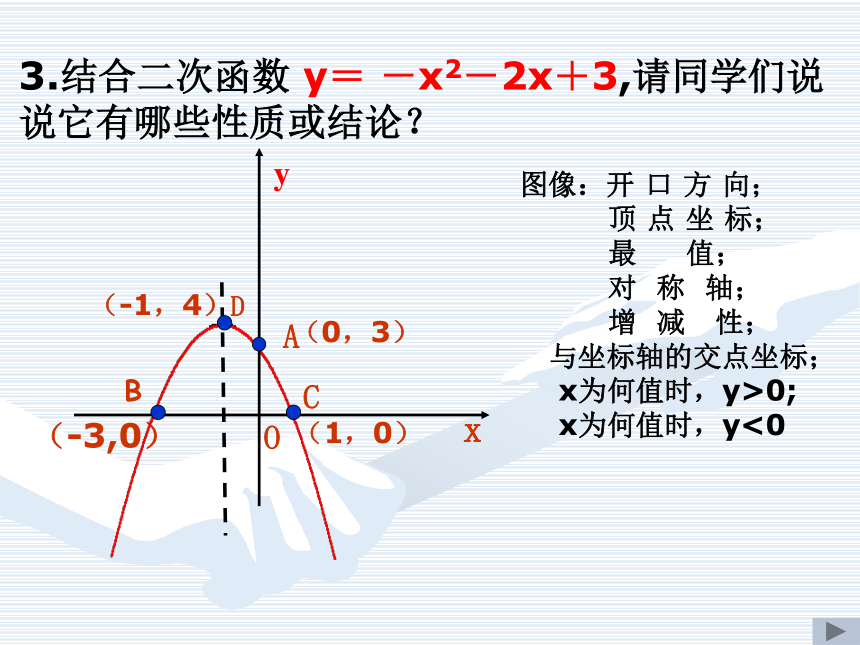
二次函数?① ② ③⑦=23.结合二次函数 y= -x2-2x+3,请同学们说说它有哪些性质或结论?
(-3,0)(-1,4)(1,0)
(0,3)
A图像:开 口 方 向;
顶 点 坐 标;
最 值;
对 称 轴;
增 减 性;
与坐标轴的交点坐标;
x为何值时,y>0;
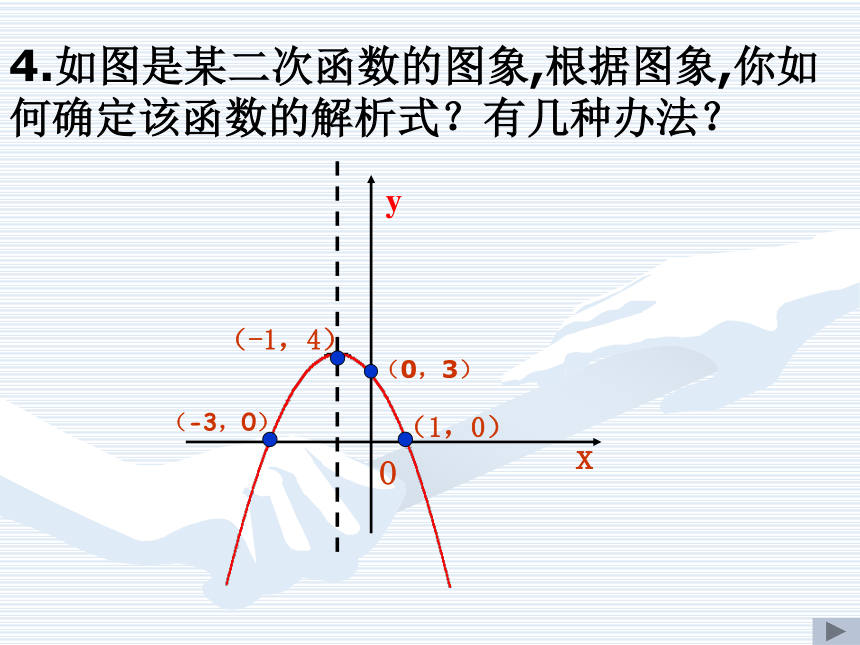
x为何值时,y<04.如图是某二次函数的图象,根据图象,你如何确定该函数的解析式?有几种办法?
请思考:解决上述问题的过程中,
我们复习了二次函数的哪些内容?
(2) 你在解题过程中运用了哪些数学思想方法?
例 、已知二次函数的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。
求该二次函数的解析式。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
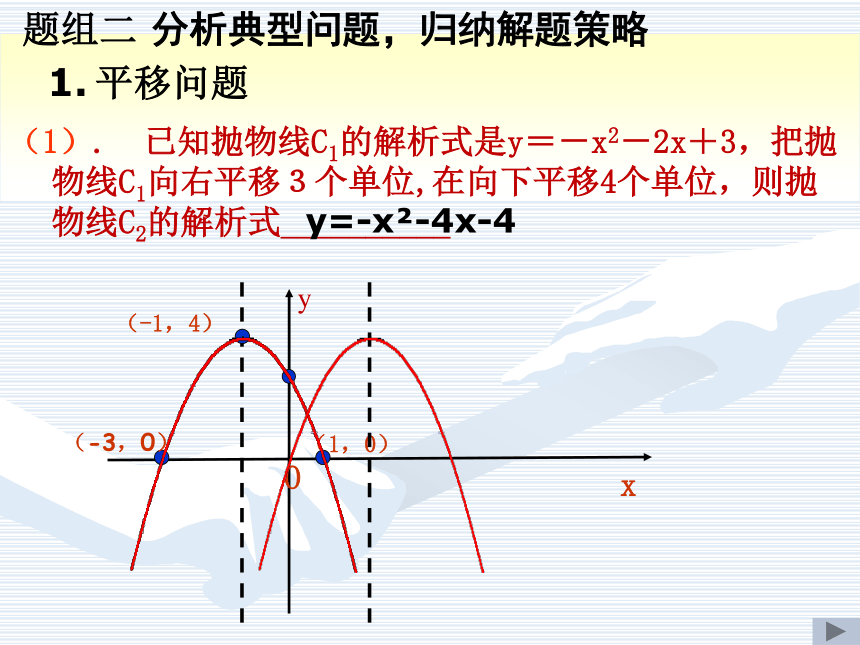
即: y=-2x2+4x(1). 已知抛物线C1的解析式是y=-x2-2x+3,把抛物线C1向右平移3个单位,在向下平移4个单位,则抛物线C2的解析式__________
y(1,0)(-1,4)xO(-3,0)平移问题题组二 分析典型问题,归纳解题策略y=-x2-4x-4例题:(2)抛物线 y=4(x-2)2-5向上平移1个单位,
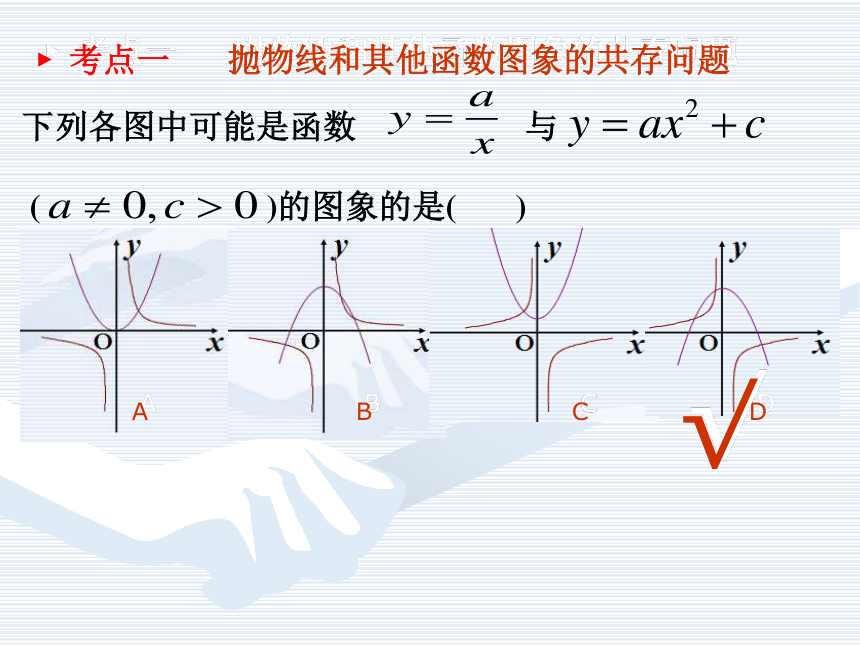
再向左平移 3个单位后解析式为 √? 考点一 抛物线和其他函数图象的共存问题 在同一直角坐标系中,一次函数y=ax+b和二次函数
y= ax2 +bx的图象可能为( )A 巩固练习 1、a 、 b 、 c
2、
3、a+b+c ;a-b+c
4 、4a-2b+c
4a+2b+c ;
5、 2a+b ; 2a-b
1? 考点二 根据图象判断系数及含有系数的代数式的符号-2数学·新课标(RJ)C C请思考:解决上述问题的过程中,
你用到了哪些解题方法?
1. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
④ b 0;xyO题组三 在练习中印证归纳结果
5 已知函数y= -x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________4 已知y=(k+2)x 是二次函数,且当x>0 时,y随X增大而增大,则k=___.K2+k-4题组三 在练习中印证归纳结果题组三 在练习中印证归纳结果6.如图,若将抛物线y=(x+1)2-7沿x轴平移,使平移后的图象经过P(-2,2),求平移后抛物线的解析式.(0,1.6)①求k的值的直角坐标系中,铅球的运行路线近似为抛物线②求铅球的落点与丁丁的距离③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?学以致用 回顾反思
1、本节课着重考查了哪些知识?
2、你又加深了对哪些数学思想方法的理解?
3、你能归纳出哪些问题的解题策略?
环节四——通过反思提升对学习过程的认知作业:
1. 必做:教材56页:复习题22 1—5小题做完
2.选做:教材66页:第 6题3.补充题:已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。欢迎指导!再见
河北保定市满城县满城镇中学题组一 梳理知识,关注数学思想方法1、下列函数中,是二次函数的是 .
① ② ③
④ ⑤ ⑥
⑦ ⑧
2.当m_______时,函数y=(m+1)χ - 2χ+1是
二次函数?① ② ③⑦=23.结合二次函数 y= -x2-2x+3,请同学们说说它有哪些性质或结论?
(-3,0)(-1,4)(1,0)
(0,3)
A图像:开 口 方 向;
顶 点 坐 标;
最 值;
对 称 轴;
增 减 性;
与坐标轴的交点坐标;
x为何值时,y>0;
x为何值时,y<04.如图是某二次函数的图象,根据图象,你如何确定该函数的解析式?有几种办法?
请思考:解决上述问题的过程中,
我们复习了二次函数的哪些内容?
(2) 你在解题过程中运用了哪些数学思想方法?
例 、已知二次函数的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。
求该二次函数的解析式。解:∵二次函数的最大值是2
∴抛物线的顶点纵坐标为2
又∵抛物线的顶点在直线y=x+1上
∴当y=2时,x=1
∴顶点坐标为( 1 , 2)
∴设二次函数的解析式为y=a(x-1)2+2
又∵图象经过点(3,-6)
∴-6=a (3-1)2+2 ∴a=-2
∴二次函数的解析式为y=-2(x-1)2+2
即: y=-2x2+4x(1). 已知抛物线C1的解析式是y=-x2-2x+3,把抛物线C1向右平移3个单位,在向下平移4个单位,则抛物线C2的解析式__________
y(1,0)(-1,4)xO(-3,0)平移问题题组二 分析典型问题,归纳解题策略y=-x2-4x-4例题:(2)抛物线 y=4(x-2)2-5向上平移1个单位,
再向左平移 3个单位后解析式为 √? 考点一 抛物线和其他函数图象的共存问题 在同一直角坐标系中,一次函数y=ax+b和二次函数
y= ax2 +bx的图象可能为( )A 巩固练习 1、a 、 b 、 c
2、
3、a+b+c ;a-b+c
4 、4a-2b+c
4a+2b+c ;
5、 2a+b ; 2a-b
1? 考点二 根据图象判断系数及含有系数的代数式的符号-2数学·新课标(RJ)C C请思考:解决上述问题的过程中,
你用到了哪些解题方法?
1. 如图,抛物线y=ax2+bx+c,请判断下列各式的符号:
①a 0;
②c 0;
③b2 - 4ac 0;
④ b 0;xyO题组三 在练习中印证归纳结果
5 已知函数y= -x2-x-4,当函数值y随x的增大而减小时,x的取值范围是___________4 已知y=(k+2)x 是二次函数,且当x>0 时,y随X增大而增大,则k=___.K2+k-4题组三 在练习中印证归纳结果题组三 在练习中印证归纳结果6.如图,若将抛物线y=(x+1)2-7沿x轴平移,使平移后的图象经过P(-2,2),求平移后抛物线的解析式.(0,1.6)①求k的值的直角坐标系中,铅球的运行路线近似为抛物线②求铅球的落点与丁丁的距离③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?学以致用 回顾反思
1、本节课着重考查了哪些知识?
2、你又加深了对哪些数学思想方法的理解?
3、你能归纳出哪些问题的解题策略?
环节四——通过反思提升对学习过程的认知作业:
1. 必做:教材56页:复习题22 1—5小题做完
2.选做:教材66页:第 6题3.补充题:已知抛物线y=ax2+bx+c与x轴正、负半轴分别交于A、B两点,与y轴负半轴交于点C。若OA=4,OB=1,∠ACB=90°,求抛物线解析式。欢迎指导!再见
同课章节目录
