1.1 动量变化与冲量的关系 课件 (共21张PPT) 高二上学期物理沪教版(2019)选择性必修第一册
文档属性
| 名称 | 1.1 动量变化与冲量的关系 课件 (共21张PPT) 高二上学期物理沪教版(2019)选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-09-26 21:54:44 | ||
图片预览






文档简介
(共21张PPT)
第1章 碰撞与动量守恒
1.动量变化与冲量的关系
教学目标
CONTENT
01
02
03
会运用动量定理
解决实际问题
推导动量定理和理解动量定理的含义
理解并掌握动量和冲量的概念
让两个鸡蛋从约1.5m高处自由落下,分别落在海绵垫上和塑料盘中
1.你会看到什么现象?
2.你能猜想一下其中的物理原理吗?
新课引入
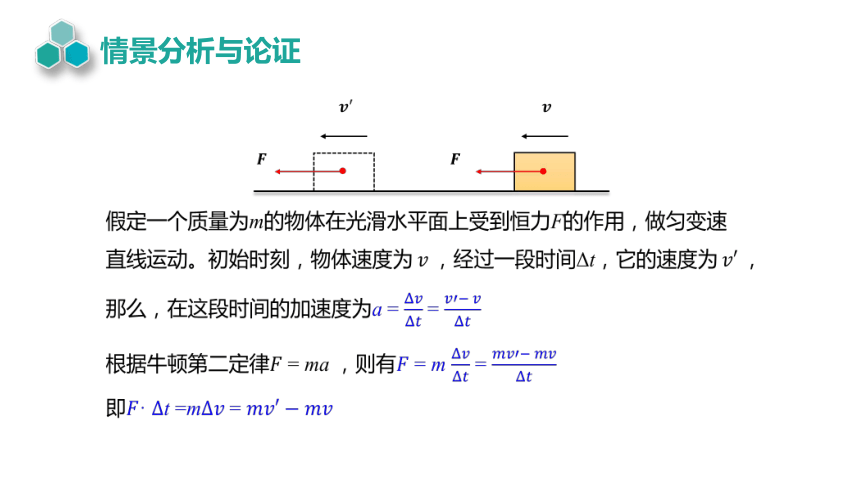
假定一个质量为m的物体在光滑水平面上受到恒力F的作用,做匀变速直线运动。初始时刻,物体速度为,经过一段时间Δt,它的速度为,那么,在这段时间的加速度为a = =
根据牛顿第二定律 = ma ,则有 = m =
即· t ==
情景分析与论证
冲量
一
知能提升
1.定义:物理学中把力和力的作用时间的乘积Ft叫做冲量,用字母 I 来表示。I = Δt
·Δt =
2.单位:在国际单位制中冲量的单位是s。
3.对冲量的理解:
(1)冲量是过程量,反映了力对时间的积累效果 。
(2)冲量是矢量,恒力冲量的方向与恒力方向一致。
动量
二
知能提升
1.定义:在物理学中,把物体的质量m和速度的乘积 mv 叫做动量 ,用 p 表示为 p = mv.
·Δt =
2.单位:在国际单位制中,动量的单位是千克米每秒,符号是kg m/s。
3.对动量的理解:
(1)动量是状态量,与某时刻对应,速度指瞬时速度 。
(2)动量是矢量,动量方向与该时刻速度方向相同。
(3)动量具有相对性,与参考系的选取有关,一般以地球为参考系,速度指对地速度。
4.动量的变化(Δ p) :
(1)物体末动量p′与初动量p的矢量差叫做物体动量的变化。
(2)表达式: Δ p = p′-p =mv'-mv = mΔv
·Δt =
(3)对动量变化的理解:
①Δ p是矢量,其方向与Δv 的方向相同。
②同一直线上动量变化的运算,可以选取正方向,以正负号代入运算。
③不在同一直线上的动量变化的运算,遵循平行四边形定则。
p
p′
p
p
p′
p
动量定理
三
知能提升
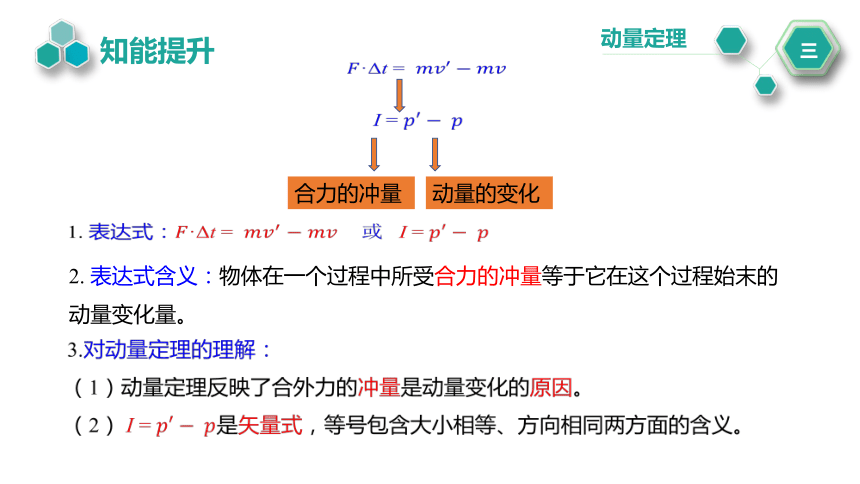
1. 表达式:·Δt = I =
·Δt =
3.对动量定理的理解:
(1)动量定理反映了合外力的冲量是动量变化的原因。
(2) I = 是矢量式,等号包含大小相等、方向相同两方面的含义。
I =
合力的冲量
动量的变化
2. 表达式含义:物体在一个过程中所受合力的冲量等于它在这个过程始末的动量变化量。
t0
F0
F
t
O
(1)求某个恒力的冲量:
如图所示,该力在时间Δt=t0-0内的冲量大小在数值上就等于图中阴影部分的“面积”。
用该力和力的作用时间的乘积。
冲量的计算
规律方法
(2)求合冲量的两种方法:
①可分别求每一个力的冲量,再求各冲量的矢量和;
②如果各个力的作用时间相同,也可以先求合力,再用公式 I合=F合t 求解。
(3)求变力的冲量:
③利用动量定理求解。I = Δ =
①若力与时间成线性关系变化,则可用平均力求变力的冲量。
②若给出了力随时间变化的图像如图所示,可用面积法求变力的冲量。
p
p′
Δ p
例1.一个质量是 0.1 kg 的钢球,以 6 m/s 的速度水平向右运动,碰到一块坚硬的障碍物后被弹回,沿着同一直线以 6 m/s 的速度水平向左运动,碰撞前后钢球的动量有没有变化?变化了多少?方向如何?
规定正方向
典例精析
解:取水平向右为正方向,设碰撞前后钢球的动量分别为p、p′,
碰撞前后钢球的动量变化为
负号表示Δp 的方向与正方向相反,即碰撞前后钢球动量改变的大小为1.2kg·m/s, 方向水平向左。
例2.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60 kg的运动员,从离水平网面3.2 m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0 m高处。已知运动员与网接触的时间为1.2 s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小。(g=10 m/s2)
解:取向上为正方向,
根据动量定理
下落到网的速度
弹起速度
解得:F=1500N
动量定理的应用
二
知能提升
旧轮胎作用?
轮船停靠码头时,靠到橡皮轮胎处,轮胎发生形变,轮胎作为缓冲装置,延长了作用时间,可以减小轮船停靠时受到的作用力。
码头上的旧轮胎
头盔
人从高处跳下
快递包装盒
铁锤钉钉子
1.质量为0.5 kg的物体,运动速度为3 m/s,它在一个变力作用下速度变为7 m/s,方向和原来方向相反,则这段时间内动量的变化量为( )
A.5 kg·m/s,方向与原运动方向相反
B.5 kg·m/s,方向与原运动方向相同
C.2 kg·m/s,方向与原运动方向相反
D.2 kg·m/s,方向与原运动方向相同
解析:以原来的运动方向为正方向,动量的变化量Δp=(-7)×0.5 kg·m/s-3×0.5 kg·m/s=-5 kg·m/s,负号表示Δp的方向与原方向相反.
A
跟踪练习
2.(多选)在任何相等时间内,物体动量的变化量总是相等的运动可能是( )
A.匀速圆周运动 B.匀变速直线运动
C.自由落体运动 D.平抛运动
解析:物体做匀变速直线运动、自由落体运动、平抛运动所受的合外力恒定不变.由动量定理可知,它们在任何相等时间内的动量变化量总相等,而物体做匀速圆周运动合外力是变力,故B、C、D均正确,A错误.
BCD
3. (多选) 把重物 G 压在纸带上,用一水平力缓缓拉动纸带,重物跟着物体一起运动,若迅速拉动纸带,纸带将会从重物下抽出,解释这些现象的正确说法是 ( )
A. 在缓慢拉动纸带时,纸带给物体的摩擦力大
B. 在迅速拉动纸带时,纸带给物体的摩擦力小
C. 在缓慢拉动纸带时,纸带给重物的冲量大
D. 在迅速拉动纸带时,纸带给重物的冲量小
CD
解析:在缓缓拉动时,两物体间的作用力是静摩擦力,在迅速拉动时,它们之间的作用力是滑动摩擦力.缓缓拉纸带时,摩擦力虽小些,但作用时间可以很长.快拉时,摩擦力虽大些,但作用时间很短,故冲量小,所以重物动量改变很小.
4.(多选)从同样高度落下的玻璃杯,掉在水泥地上容易打碎,而掉在草地上不容易打碎,其原因是( )
A.掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小
B.掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小
C.掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢
D.掉在水泥地上的玻璃杯与地面接触时,相互作用时间短,而掉在草地
上的玻璃杯与地面接触时,相互作用时间长
CD
解析:因为初始高度一样,接触水泥地和草地时动量相等;最终都会静止,所以接触水泥地和接触草地过程动量改变量也相等;但接触水泥地过程时间短,动量改变快,接触草地过程时间长,动量改变慢。
5.假设与国航波音737相撞的这只飞鸟的质量为1 kg,以20 m/s的速度,水平迎面撞上速度为720km/h的波音737飞机并粘在飞机上,而飞机并没有因为与鸟相撞而立即改变速度。试求,这只疯狂的小鸟撞上航天飞机前后的动量的改变?撞击时间约为0.01s,撞击力多大?
解:取飞鸟运动的方向为正方向
碰撞前:p0=mv0=20kg m/s
碰撞后:vt=-720km/h =-200m/s
p′ =mv =-200kg m/s
Δp= p′ - p0 =-220kg m/s
方向与飞鸟飞行的方向相反
F=Δp/ Δt=-22000N
方向与飞鸟飞行的方向相反
本节内容结束
第1章 碰撞与动量守恒
1.动量变化与冲量的关系
教学目标
CONTENT
01
02
03
会运用动量定理
解决实际问题
推导动量定理和理解动量定理的含义
理解并掌握动量和冲量的概念
让两个鸡蛋从约1.5m高处自由落下,分别落在海绵垫上和塑料盘中
1.你会看到什么现象?
2.你能猜想一下其中的物理原理吗?
新课引入
假定一个质量为m的物体在光滑水平面上受到恒力F的作用,做匀变速直线运动。初始时刻,物体速度为,经过一段时间Δt,它的速度为,那么,在这段时间的加速度为a = =
根据牛顿第二定律 = ma ,则有 = m =
即· t ==
情景分析与论证
冲量
一
知能提升
1.定义:物理学中把力和力的作用时间的乘积Ft叫做冲量,用字母 I 来表示。I = Δt
·Δt =
2.单位:在国际单位制中冲量的单位是s。
3.对冲量的理解:
(1)冲量是过程量,反映了力对时间的积累效果 。
(2)冲量是矢量,恒力冲量的方向与恒力方向一致。
动量
二
知能提升
1.定义:在物理学中,把物体的质量m和速度的乘积 mv 叫做动量 ,用 p 表示为 p = mv.
·Δt =
2.单位:在国际单位制中,动量的单位是千克米每秒,符号是kg m/s。
3.对动量的理解:
(1)动量是状态量,与某时刻对应,速度指瞬时速度 。
(2)动量是矢量,动量方向与该时刻速度方向相同。
(3)动量具有相对性,与参考系的选取有关,一般以地球为参考系,速度指对地速度。
4.动量的变化(Δ p) :
(1)物体末动量p′与初动量p的矢量差叫做物体动量的变化。
(2)表达式: Δ p = p′-p =mv'-mv = mΔv
·Δt =
(3)对动量变化的理解:
①Δ p是矢量,其方向与Δv 的方向相同。
②同一直线上动量变化的运算,可以选取正方向,以正负号代入运算。
③不在同一直线上的动量变化的运算,遵循平行四边形定则。
p
p′
p
p
p′
p
动量定理
三
知能提升
1. 表达式:·Δt = I =
·Δt =
3.对动量定理的理解:
(1)动量定理反映了合外力的冲量是动量变化的原因。
(2) I = 是矢量式,等号包含大小相等、方向相同两方面的含义。
I =
合力的冲量
动量的变化
2. 表达式含义:物体在一个过程中所受合力的冲量等于它在这个过程始末的动量变化量。
t0
F0
F
t
O
(1)求某个恒力的冲量:
如图所示,该力在时间Δt=t0-0内的冲量大小在数值上就等于图中阴影部分的“面积”。
用该力和力的作用时间的乘积。
冲量的计算
规律方法
(2)求合冲量的两种方法:
①可分别求每一个力的冲量,再求各冲量的矢量和;
②如果各个力的作用时间相同,也可以先求合力,再用公式 I合=F合t 求解。
(3)求变力的冲量:
③利用动量定理求解。I = Δ =
①若力与时间成线性关系变化,则可用平均力求变力的冲量。
②若给出了力随时间变化的图像如图所示,可用面积法求变力的冲量。
p
p′
Δ p
例1.一个质量是 0.1 kg 的钢球,以 6 m/s 的速度水平向右运动,碰到一块坚硬的障碍物后被弹回,沿着同一直线以 6 m/s 的速度水平向左运动,碰撞前后钢球的动量有没有变化?变化了多少?方向如何?
规定正方向
典例精析
解:取水平向右为正方向,设碰撞前后钢球的动量分别为p、p′,
碰撞前后钢球的动量变化为
负号表示Δp 的方向与正方向相反,即碰撞前后钢球动量改变的大小为1.2kg·m/s, 方向水平向左。
例2.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60 kg的运动员,从离水平网面3.2 m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0 m高处。已知运动员与网接触的时间为1.2 s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小。(g=10 m/s2)
解:取向上为正方向,
根据动量定理
下落到网的速度
弹起速度
解得:F=1500N
动量定理的应用
二
知能提升
旧轮胎作用?
轮船停靠码头时,靠到橡皮轮胎处,轮胎发生形变,轮胎作为缓冲装置,延长了作用时间,可以减小轮船停靠时受到的作用力。
码头上的旧轮胎
头盔
人从高处跳下
快递包装盒
铁锤钉钉子
1.质量为0.5 kg的物体,运动速度为3 m/s,它在一个变力作用下速度变为7 m/s,方向和原来方向相反,则这段时间内动量的变化量为( )
A.5 kg·m/s,方向与原运动方向相反
B.5 kg·m/s,方向与原运动方向相同
C.2 kg·m/s,方向与原运动方向相反
D.2 kg·m/s,方向与原运动方向相同
解析:以原来的运动方向为正方向,动量的变化量Δp=(-7)×0.5 kg·m/s-3×0.5 kg·m/s=-5 kg·m/s,负号表示Δp的方向与原方向相反.
A
跟踪练习
2.(多选)在任何相等时间内,物体动量的变化量总是相等的运动可能是( )
A.匀速圆周运动 B.匀变速直线运动
C.自由落体运动 D.平抛运动
解析:物体做匀变速直线运动、自由落体运动、平抛运动所受的合外力恒定不变.由动量定理可知,它们在任何相等时间内的动量变化量总相等,而物体做匀速圆周运动合外力是变力,故B、C、D均正确,A错误.
BCD
3. (多选) 把重物 G 压在纸带上,用一水平力缓缓拉动纸带,重物跟着物体一起运动,若迅速拉动纸带,纸带将会从重物下抽出,解释这些现象的正确说法是 ( )
A. 在缓慢拉动纸带时,纸带给物体的摩擦力大
B. 在迅速拉动纸带时,纸带给物体的摩擦力小
C. 在缓慢拉动纸带时,纸带给重物的冲量大
D. 在迅速拉动纸带时,纸带给重物的冲量小
CD
解析:在缓缓拉动时,两物体间的作用力是静摩擦力,在迅速拉动时,它们之间的作用力是滑动摩擦力.缓缓拉纸带时,摩擦力虽小些,但作用时间可以很长.快拉时,摩擦力虽大些,但作用时间很短,故冲量小,所以重物动量改变很小.
4.(多选)从同样高度落下的玻璃杯,掉在水泥地上容易打碎,而掉在草地上不容易打碎,其原因是( )
A.掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小
B.掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小
C.掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢
D.掉在水泥地上的玻璃杯与地面接触时,相互作用时间短,而掉在草地
上的玻璃杯与地面接触时,相互作用时间长
CD
解析:因为初始高度一样,接触水泥地和草地时动量相等;最终都会静止,所以接触水泥地和接触草地过程动量改变量也相等;但接触水泥地过程时间短,动量改变快,接触草地过程时间长,动量改变慢。
5.假设与国航波音737相撞的这只飞鸟的质量为1 kg,以20 m/s的速度,水平迎面撞上速度为720km/h的波音737飞机并粘在飞机上,而飞机并没有因为与鸟相撞而立即改变速度。试求,这只疯狂的小鸟撞上航天飞机前后的动量的改变?撞击时间约为0.01s,撞击力多大?
解:取飞鸟运动的方向为正方向
碰撞前:p0=mv0=20kg m/s
碰撞后:vt=-720km/h =-200m/s
p′ =mv =-200kg m/s
Δp= p′ - p0 =-220kg m/s
方向与飞鸟飞行的方向相反
F=Δp/ Δt=-22000N
方向与飞鸟飞行的方向相反
本节内容结束
同课章节目录
- 第1章 碰撞与动量守恒
- 1.1 动量变化与冲量的关系
- 1.2 动量守恒定律
- 1.3 动量守恒定律的案例分析
- 1.4 美妙的守恒定律
- 第2章 机械振动
- 2.1 简谐运动
- 2.2 物体做简谐运动的原因
- 2.3 摆钟的物理原理
- 2.4 单摆振动的周期
- 2.5 受迫振动与共振
- 第3章 机械波
- 3.1 机械波的产生
- 3.2 机械波的描述
- 3.3 机械波案例分析
- 3.4 惠更斯原理 波的反射与折射
- 3.5 波的干涉与衍射
- 3.6 多普勒效应
- 第4章 光及其应用
- 4.1 光的折射
- 4.2 全反射与光导纤维
- 4.3 光的干涉
- 4.4 用双缝干涉仪测量光的波长
- 4.5 光的衍射
- 4.6 光的偏振与立体电影
- 4.7 激光
