2.4.1圆的标准方程 课件(共16张PPT)
文档属性
| 名称 | 2.4.1圆的标准方程 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 803.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-26 18:19:22 | ||
图片预览





文档简介
(共16张PPT)
第二章 直线和圆的方程
2.4 圆的方程
课时1 圆的标准方程
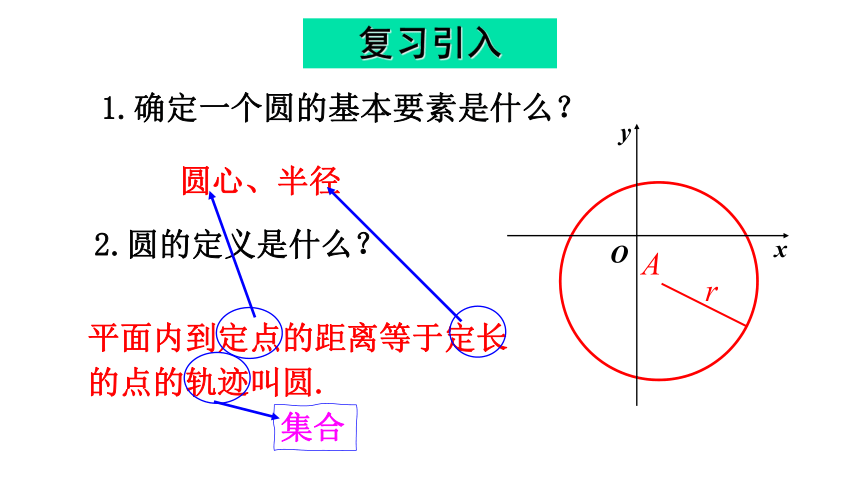
圆心、半径
1.确定一个圆的基本要素是什么?
2.圆的定义是什么?
平面内到定点的距离等于定长的点的轨迹叫圆.
A
r
x
y
O
集合
复习引入
根据两点间距离公式,即
_________________
在平面直角坐标系中,如何确定圆的方程呢?
两边平方,得
____________________
|MC|与r的关系:_______
|MC|=r
M(x, y)
C(a,b)
设圆心C(a,b)和圆上动点M(x,y),半径为r.
x
y
O
探究1 圆的标准方程
(1)
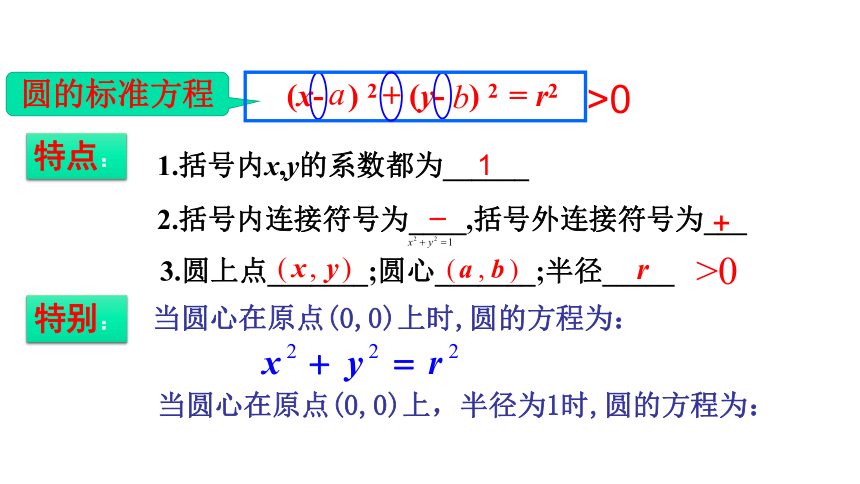
1.括号内x,y的系数都为______
2.括号内连接符号为____,括号外连接符号为___
特点:
特别:
圆的标准方程
(x- ) 2 + (y- ) 2 = r2
>0
3.圆上点_______;圆心_______;半径_____
1
-
+
当圆心在原点(0,0)上时,圆的方程为:
>0
当圆心在原点(0,0)上,半径为1时,圆的方程为:
习题: 1.判断下列方程是圆的方程吗?
2.根据圆的标准方程,求出圆心和半径.
(1)圆
的圆心是______,半径是___
(2)圆
的圆心是______,半径是____
(3)圆
的圆心是_____,半径是____
(3, 4)
(-3, 1)
3.已知圆心和半径,写出圆的标准方程
(1)圆心为(1, 2),半径为2,___________________
(2)圆心为(-1, 2),半径为1,__________________
(3)圆心为(1, -2),半径为 , ____________________
例1 写出圆心为A(2,3),半径长等于5的圆的方程,并判断点M1(5,7),M2(-2,-1)是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
例题讲解
把点 的坐标代入此方程,左右两边不相等,点 的坐标不满足圆的方程,所以点 不在这个圆上.
圆A:(x-a)2+(y-b)2=r2(r>0),其圆心为A(a,b),半径为r,点P(x0,y0),设d=|PA|
位置关系 几何法 图示 代数法
点在圆外 d>r (x0-a)2+(y0-b)2>r2
点在圆上 d=r (x0-a)2+(y0-b)2=r2
点在圆内 d<r (x0-a)2+(y0-b)2点与圆的位置关系
A.在圆外 B.在圆上 C.在圆内 D.在圆上或圆外
(1)点P(3,2)与圆(x-2)2+(y-3)2=4的位置关系( )
C
(2)点P(m,5)与圆x2+y2=25的位置关系( )
D
A.在圆外 B.在圆上 C.在圆内 D.在圆上或圆外
习题:判断点与圆的位置关系
A.-4(3)已知点P(a,a+1)在圆x2+y2=25的内部,则a的取值范围是( )
A
(1)判断点与圆的位置关系的方法:①只需计算该点与圆心的距离,与半径作比较即可;②把点的坐标代入圆的标准方程,判断式子两边的符号,并作出判断.
(2)若已知点与圆的位置关系,也可利用以上两种方法列出不等式或方程,求解参数的取值范围.
课本85页第1题
解:设所求圆的方程为:
因为A(5,1), B(7,-3),C(2,-8)都在圆上,所以有
所求圆的方程为:
例2 △ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8), 求它的外接圆的方程.
解得
例题讲解
待定系数法
解法1:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
设圆C的方程为
∵圆心在直线 l: x-y+1=0上,且圆经过A(1,1),B(2,-2)
例题讲解
解法2:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
一题多解
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
解法3: ∵ A(1,1),B(2,-2)
∴圆心C(-3,-2)
一题多解
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
圆的标准方程
圆心、半径
点与圆的位置关系
圆外:
圆上:
圆内:
通过今天的学习,你学到了哪些新知识?
在今天的学习中,运用了什么数学方法与思想?
类比法、坐标法、代数法、数形结合等
圆的基本要素
课堂小结
*注:特别的,圆心在坐标原点,半径长为r 的圆的方程是
A
x
y
o
M2
M3
M1
第二章 直线和圆的方程
2.4 圆的方程
课时1 圆的标准方程
圆心、半径
1.确定一个圆的基本要素是什么?
2.圆的定义是什么?
平面内到定点的距离等于定长的点的轨迹叫圆.
A
r
x
y
O
集合
复习引入
根据两点间距离公式,即
_________________
在平面直角坐标系中,如何确定圆的方程呢?
两边平方,得
____________________
|MC|与r的关系:_______
|MC|=r
M(x, y)
C(a,b)
设圆心C(a,b)和圆上动点M(x,y),半径为r.
x
y
O
探究1 圆的标准方程
(1)
1.括号内x,y的系数都为______
2.括号内连接符号为____,括号外连接符号为___
特点:
特别:
圆的标准方程
(x- ) 2 + (y- ) 2 = r2
>0
3.圆上点_______;圆心_______;半径_____
1
-
+
当圆心在原点(0,0)上时,圆的方程为:
>0
当圆心在原点(0,0)上,半径为1时,圆的方程为:
习题: 1.判断下列方程是圆的方程吗?
2.根据圆的标准方程,求出圆心和半径.
(1)圆
的圆心是______,半径是___
(2)圆
的圆心是______,半径是____
(3)圆
的圆心是_____,半径是____
(3, 4)
(-3, 1)
3.已知圆心和半径,写出圆的标准方程
(1)圆心为(1, 2),半径为2,___________________
(2)圆心为(-1, 2),半径为1,__________________
(3)圆心为(1, -2),半径为 , ____________________
例1 写出圆心为A(2,3),半径长等于5的圆的方程,并判断点M1(5,7),M2(-2,-1)是否在这个圆上.
解:圆心是 ,半径长等于5的圆的标准方程是:
把 的坐标代入方程 左右两边相等,点 的坐标适合圆的方程,所以点 在这个圆上;
例题讲解
把点 的坐标代入此方程,左右两边不相等,点 的坐标不满足圆的方程,所以点 不在这个圆上.
圆A:(x-a)2+(y-b)2=r2(r>0),其圆心为A(a,b),半径为r,点P(x0,y0),设d=|PA|
位置关系 几何法 图示 代数法
点在圆外 d>r (x0-a)2+(y0-b)2>r2
点在圆上 d=r (x0-a)2+(y0-b)2=r2
点在圆内 d<r (x0-a)2+(y0-b)2
A.在圆外 B.在圆上 C.在圆内 D.在圆上或圆外
(1)点P(3,2)与圆(x-2)2+(y-3)2=4的位置关系( )
C
(2)点P(m,5)与圆x2+y2=25的位置关系( )
D
A.在圆外 B.在圆上 C.在圆内 D.在圆上或圆外
习题:判断点与圆的位置关系
A.-4
A
(1)判断点与圆的位置关系的方法:①只需计算该点与圆心的距离,与半径作比较即可;②把点的坐标代入圆的标准方程,判断式子两边的符号,并作出判断.
(2)若已知点与圆的位置关系,也可利用以上两种方法列出不等式或方程,求解参数的取值范围.
课本85页第1题
解:设所求圆的方程为:
因为A(5,1), B(7,-3),C(2,-8)都在圆上,所以有
所求圆的方程为:
例2 △ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8), 求它的外接圆的方程.
解得
例题讲解
待定系数法
解法1:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
设圆C的方程为
∵圆心在直线 l: x-y+1=0上,且圆经过A(1,1),B(2,-2)
例题讲解
解法2:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
一题多解
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
解法3: ∵ A(1,1),B(2,-2)
∴圆心C(-3,-2)
一题多解
圆的标准方程的两种求法
(1)几何法 它是利用图形的几何性质,如圆的性质等,直接求出圆的圆心和半径,代入圆的标准方程,从而得到圆的标准方程.
(2)待定系数法
由三个独立条件得到三个方程,解方程组以得到圆的标准方程中三个参数,从而确定圆的标准方程.它是求圆的方程最常用的方法,一般步骤是:①设——设所求圆的方程为(x-a)2+(y-b)2=r2;
②列——由已知条件,建立关于a,b,r的方程组;
③解——解方程组,求出a,b,r;
④代——将a,b,r代入所设方程,得所求圆的方程.
圆的标准方程
圆心、半径
点与圆的位置关系
圆外:
圆上:
圆内:
通过今天的学习,你学到了哪些新知识?
在今天的学习中,运用了什么数学方法与思想?
类比法、坐标法、代数法、数形结合等
圆的基本要素
课堂小结
*注:特别的,圆心在坐标原点,半径长为r 的圆的方程是
A
x
y
o
M2
M3
M1
