方程的根与函数的零点

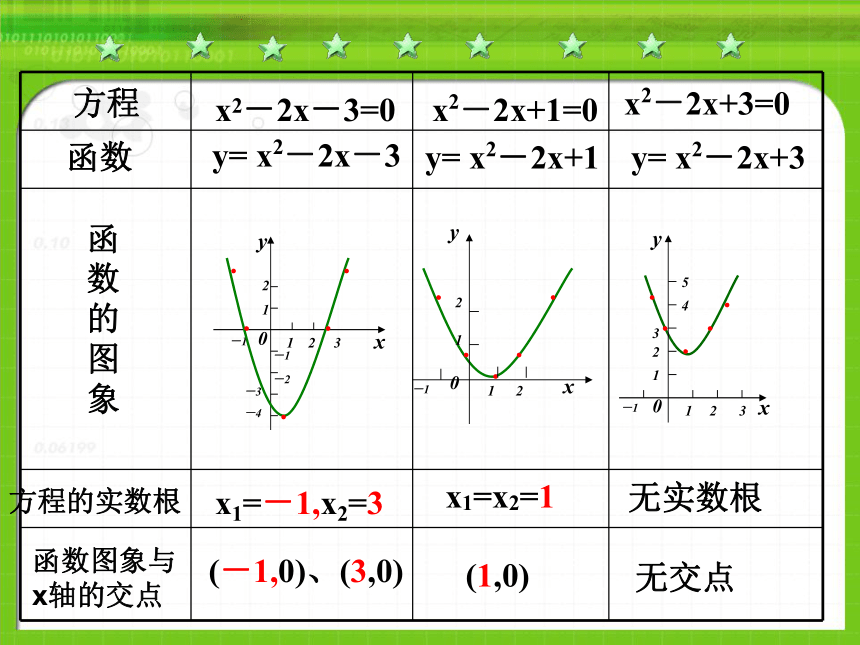
课件12张PPT。 方程的根 和 函数的零点问题情境:(1)y=x2-2x-3与x2-2x-3=0(2)y=x2-2x+1与x2-2x+1=0(3)y=x2-2x+3与x2-2x+3=0下列二次函数的图象与x轴交点和相应方程的根有何关系？方程x2－2x+1=0x2－2x+3=0y= x2－2x－3y= x2－2x+1函数函
数
的
图
象方程的实数根x1=－1,x2=3x1=x2=1无实数根(－1,0)、(3,0)(1,0)无交点x2－2x－3=0y= x2－2x+3函数图象与
x轴的交点 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。函数零点的定义：注意：零点指的是一个实数；推广引申:
对于一般的二次函数y=ax2+bx+c(a≠0)和一元二次方程ax2+bx+c=0(a≠0),上述三者关系还成立吗?方程f(x)=0的实数根等价关系进一步推广练习2、求函数y=x2-5x+6的零点。练一练:练习1、求函数y=2x+6的零点。变式:求函数y=kx+b(k≠0)的零点。012345-1-212345-1-2-3-4xy探究 归纳：函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点，即存在c∈(a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根。建构新知判一判总结：函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线：练习4、求证：方程5x2-7x-1=0的一个根在区间
(-1,0)内，另一个根在区间(1,2)内。变式：若函数y=5x2-7x-1在区间[a,b]上的图象是
连续不断的曲线，且函数y=5x2-7x-1在(a,b)内有
零点，则f(a)·f(b)的值( )
A、大于0 B、小于0 C、无法判断 D、等于0例1、求函数f(x)=lnx+2x-6的零点的个数。例题分析小结：1、函数y=f(x)的零点的定义。2、三个等价关系。3、函数y=f(x)的零点存在性的判定。4、学会数形结合和函数与方程的思想。函数零点方程根，
形数本是同根生。
函数零点端点判，
图象连续不能忘。