11.1 与三角形有关的线段本节综合检测题(含解析)
文档属性
| 名称 | 11.1 与三角形有关的线段本节综合检测题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 08:06:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
11.1 与三角形有关的线段本节综合检测题
一、填空题
1.已知三角形的三边分别为2,x,3,那么x的取值范围是
2.如图,在平面直角坐标系中,点A在x轴上,点B(0,9),线段AB向右平移3个单位至线段CD,线段CD与y轴交于点E,若图中阴影部分面积是21,则点C的坐标为 .
二、单选题
3.现有两根木棒,它们长分别是40cm和50cm,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10cm的木棒 B.40cm的木棒 C.90cm的木棒 D.100cm的木棒
4.若一个三角形的两边长分别为3cm和7cm,则第三边长可能是( )
A.4cm B.9cm C.10cm D.11cm
5.以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
6.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
7.下列各组数据表示三条线段的长。以各组线段为边,不能构成三角形的是( )
A.5,12,13 B.7,24,25 C.1,2,3 D.6,6,6
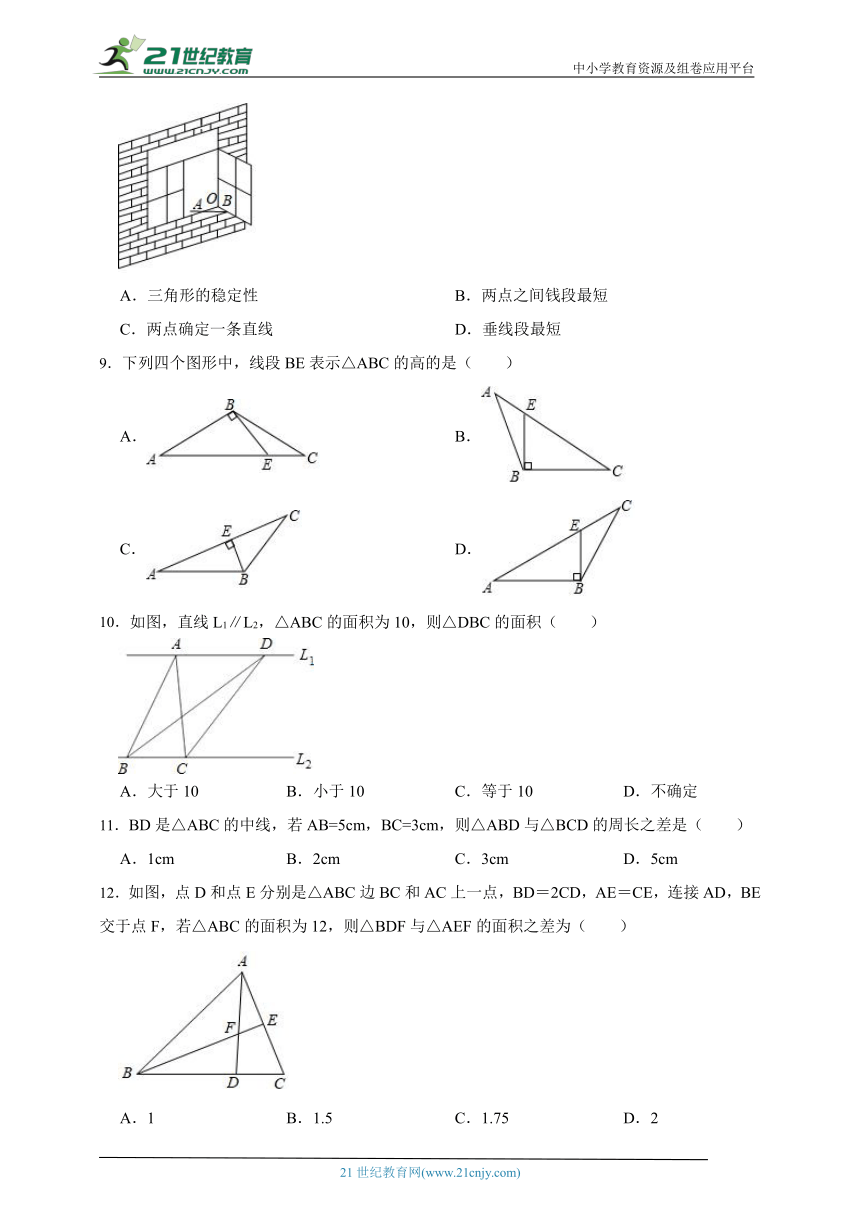
8.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间钱段最短
C.两点确定一条直线 D.垂线段最短
9.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
10.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
11.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是( )
A.1cm B.2cm C.3cm D.5cm
12.如图,点D和点E分别是△ABC边BC和AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为12,则△BDF与△AEF的面积之差为( )
A.1 B.1.5 C.1.75 D.2
三、解答题
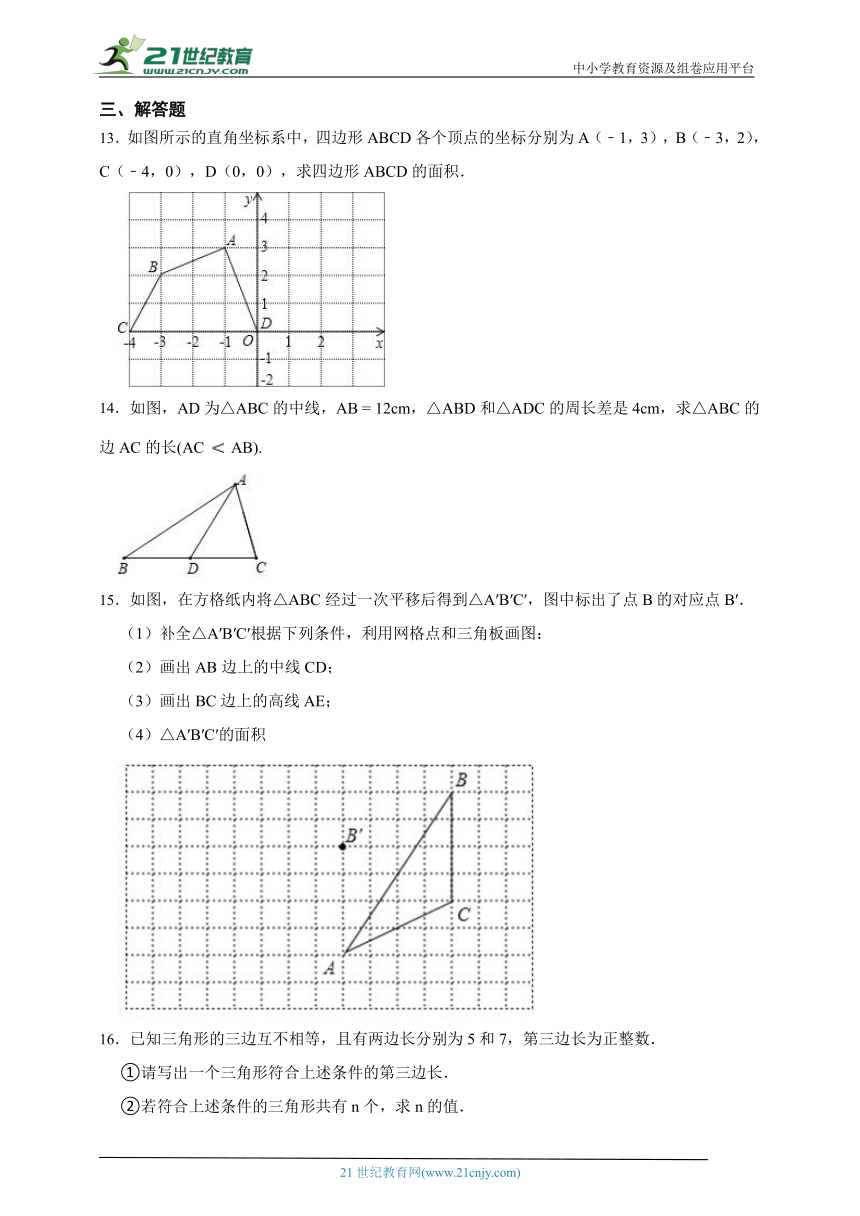
13.如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(﹣1,3),B(﹣3,2),C(﹣4,0),D(0,0),求四边形ABCD的面积.
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积
16.已知三角形的三边互不相等,且有两边长分别为5和7,第三边长为正整数.
①请写出一个三角形符合上述条件的第三边长.
②若符合上述条件的三角形共有n个,求n的值.
③试求出②中这n个三角形的周长为偶数的三角形所占的比例.
四、计算题
17.已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
五、综合题
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求:
(1)∠BCD的度数;
(2)∠ECD的度数.
19.如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.在平面直角坐标系 中,对于点 ,若点 的坐标为 ,则称点是的“ 演化点”.例如,点 的“ 演化点”为 ,即 .
(1)已知点 的“ 演化点”是 ,则 的坐标为 ;
(2)已知点 ,且点 的“ 演化点”是 ,则 的面积 为 ;
(3)已知 , , , ,且点 的“ 演化点”为 ,当 时, .
六、实践探究题
21.阅读材料;若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴m=4,n=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0.则2x+3y的值为 ;
(2)已知△ABC的边长a、b、c是三个互不相等的正整数,且满足a2+b2﹣4a﹣6b+13=0,求c的值;(写出求解过程)
(3)已知a﹣b=10,ab+c2﹣16c+89=0,则a+b+c的值为 .
22.综合与实践
【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点是BC边上的中点,连接AD.求证:.
证明:过点作于
(1)【拓展探究】
如图2,在△ABC中,点D是BC边上的中点中,点是BC边上的中点,若,则 .
(2)如图3,在中,点是BC边上的点且和存在怎样的数量关系 请模仿写出证明过程.
(3)【问题解决】
现在有一块四边形土地ABCD(如图4),能大和都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
答案解析部分
1.【答案】1<x<5
【解析】【解答】解:由题意得:3-2<x<3+2,
即1<x<5.
故答案为:1<x<5.
【分析】根据三角形三边关系(两边之和大于第三边,两边之差小于第三边)列出不等式组,解这个不等式组即可.
2.【答案】
【解析】【解答】解:连接BC,AE,设OE=x,OC=y.
∵CE∥AB,
∴S△ACB=S△ABE,
∴×3×9=×(9 x)×(3+y) ①,
又∵×(3+y)×9 xy=21 ②,
联立①与②得x=5,y=,
∴C点坐标为.
故答案为:.
【分析】连接BC,AE,设OE=x,OC=y.根据平移的性质得AB∥CD,再根据等底同高的三角形的面积相等得S△ACB=S△ABE,进而根据三角面积计算方法建立方程组,求解即可.
3.【答案】B
【解析】【解答】已知三角形的两边是40cm和50cm,则
10<第三边<90.
故答案为:40cm的木棒.
故答案为:B.
【分析】利用三角形三边的关系可得10<第三边<90,再求解即可。
4.【答案】B
【解析】【解答】解:设第三边长为x cm,根据三角形的三边关系可得:7-3<x<7+3,
解得:4<x<10,
∴第三边长可能是9cm.
故答案为:B.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边长的范围,然后结合各个选项中的数据进行判断.
5.【答案】B
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
6.【答案】B
【解析】【解答】解: ①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故答案为:B.
【分析】根据三角形的三条中线,三条角平分线,三条高的位置判断.
三角形的三条中线都在三角形内部;
三角形的三条角平分线都在三角形内部;
三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上.
7.【答案】C
【解析】【分析】三角形的基本关系满足,两边之和大于第三边,两边之差小于第三边,本题中唯一不能构成三角形的是C,不满足三角形的三边的基本关系,故选C.
【点评】本题属于对三角形的三边的基本关系的理解和运用。
8.【答案】A
【解析】【解答】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.故答案为:A
【分析】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.
9.【答案】C
【解析】【解答】解:线段BE是△ABC的高的图是选项C.
故答案为:C.
【分析】根据高的定义对每个选项一一判断求解即可。
10.【答案】C
【解析】【解答】解:∵L1∥L2,
∴L1,L2之间的距离是固定的,
∴△ABC和△DBC的BC边上的高相等,
∴△ABC和△DBC的面积相等,
∴△DBC的面积等于10.
故选C.
【分析】由于平行线间的距离处处相等,而△ABC和△DBC的BC边上的高相等,所以△ABC和△DBC的面积相等,即可求出答案.
11.【答案】B
【解析】【解答】解:
∵BD是△ABC的中线,
∴AD=CD,
∵△ABD周长=AB+AD+BD,△BCD周长=BC+CD+BD,
∴△ABD周长﹣△BCD周长=(AB+AD+BD)﹣(BC+CD+BD)=AB﹣BC=5﹣3=2(cm),
即△ABD和△BCD的周长之差是2cm,
故选B.
【分析】利用中线的定义可知AD=CD,可知△ABD和△BCD的周长之差即为AB和BC的差,可求得答案.
12.【答案】D
【解析】【解答】解:设BC边的高为hBC,AC边的高为hAC,
∵S△ABC=BC hBC=AC hAC=12,
∴S△ABC=(BD+CD) hBC=(AE+CE) hAC=12,
∵AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,
∴S△AEB=S△CEB=S△ABC=×12=6,
即S△AEF+S△ABF=6①,
∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD hBC,
∴S△ABD=S△ABC=×12=8,
即S△BDF+S△ABF=8②,
②﹣①得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=8﹣6=2,
故答案为:D.
【分析】设BC边的高为hBC,AC边的高为hAC,根据S△ABC=BC hBC,得出S△ABC=12,根据AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,S△AEB=6,即S△AEF+S△ABF=6①,再得出S△ABD=8,即S△BDF+S△ABF=8②,利用②﹣①即可得解。
13.【答案】解:四边形ABCD的面积= ×1×2+ ×(2+3)×2+ ×1×3=1+5+1.5=7.5.
故四边形ABCD的面积为7.5
【解析】【分析】把四边形ABCD分成两个直角三角形和一个直角梯形,然后根据点的坐标和三角形面积公式与梯形面积公式进行计算即可.
14.【答案】解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
【解析】【分析】根据三角形中线的定义得出BD = CD, 再根据△ABD和△ADC的周长差是4cm列出等式,化简得出AB – AC = 4cm, 即可求出AC的长.
15.【答案】解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
故答案为:8.
【解析】【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
16.【答案】【解答】两边长分别为5和7,设第三边是a,则7-5<a<7+5,即2<a<12.①第三边长是3.(答案不唯一);②∵2<a<12,∴n=7;③周长为偶数的三角形个数是4,周长为偶数的三角形所占的比例为4:7.
【解析】【分析】①根据三角形三边关系求得第三边的取值范围,即可求解;
②找到第三边的取值范围内的正整数的个数,即为所求;
③用周长为偶数的三角形个数÷三角形的总个数,列式计算即可求解.
17.【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
18.【答案】(1)解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°
(2)解:∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=50°-30°=20°
【解析】【分析】(1)根据垂直的定义得出 ∠CDB=90°, 根据直角三角形的两锐角互余得出 ∠BCD=90°-∠B=30° ;
(2)根据三角形的内角和得出 ∠ACB=100°, 根据角平分线的定义得出 ∠BCE= ∠ACB=50°, 最后根据角的和差,由 ∠ECD=∠BCE-∠BCD 算出答案。
19.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)
(2)解:标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为= ×5×4=10
【解析】【分析】(1)根据学校的位置可建立直角坐标系,进而写出图书馆B位置的坐标;
(2)根据C的坐标可得体育馆的位置,然后连接A、B、C,接下来根据三角形的面积公式计算即可.
20.【答案】(1)(2,14)
(2)20
(3)
【解析】【解答】解:(1)由题意可知:点 的“ 演化点”是 ,即 ,
故答案为:(2,14);
( 2 )设Q点坐标为(x,y),由题意可知: ,解得:
∴Q点坐标为(0,4)
∴
故答案为:20;
( 3 )由题意可知:AD=3,OC=5
的坐标为 ,即点 的坐标为
当点 位于y轴正半轴时, ,
∴ 或 (此情况不合题意,舍去)
又∵
∴ ,解得: (舍去)
当点 位于y轴正半轴时, ,
∴
又∵
∴ ,解得: ,即
故答案为: .
【分析】(1)根据题意a=3,x=-1,y=5时,求点 的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出 ,然后分点 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
21.【答案】(1)-1
(2)解:∵a2+b2﹣4a﹣6b+13=a2﹣4a+4+b2﹣6b+9=(a﹣2)2+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
∴a=2,b=3,
∵a、b、c是△ABC的三边,
∴1<c<5,
∵a、b、c是三个互不相等的正整数,
∴c=4;
(3)8
【解析】【解答】解:(1)∵x2+2xy+2y2+2y+1=x2+2xy+y2+y2+2y+1=(x+y)2+(y+1)2=0,
∴(x+y)2=0,(y+1)2=0,
∴y=﹣1,x=1,
∴2x+3y=2×1+3×(-1)=﹣1;
(3)∵a﹣b=10,即a=b+10,代入得:b(b+10)+c2﹣16c+89=0,
整理得:(b2+10b+25)+(c2﹣16c+64)=(b+5)2+(c﹣8)2=0,
∴b+5=0,c﹣8=0,
解得b=﹣5,c=8,
则a=5,
则a+b+c=5﹣5+8=8.
【分析】(1)对已知等式进行变形可得(x+y)2+(y+1)2=0,根据偶次幂的非负性可得x+y=0、y+1=0,求出x、y的值,然后代入2x+3y中进行计算;
(2)对已知等式进行变形可得(a-2)2+(b-3)2=0,根据偶次幂的非负性可得a-2=0、b-3=0,求出a、b的值,结合三角形的三边关系求出c的范围,根据a、b、c是三个互不相等的正整数就可得到c的值;
(3)由已知条件可得a=b+10,代入等式中并整理可得(b+5)2+(c-8)2=0,根据偶次幂的非负性可得b+5=0,c﹣8=0,求出a、b、c的值,然后根据有理数的加法法则进行计算.
22.【答案】(1)3
(2);理由如下:
过点A作AE⊥BC于E
∵CD=2BD
∴AC=3BD
∴
(3)方法一:如图,连接BD,取BD的中点,连接AE,BE,则四边形ADEC就是四边形ABCD的一半。
方法二:如图,取AD的中点H、取BC的中点F,连接AF,CH,则四边形AFCH就是四边形ABCD的一半。
【解析】【解答】解:(1)∵点D是BC边上的中点,
∴AD是 △ ABC的中线,
∴,
∵,
∴,
故答案为:3.
(2),
理由如下:作AE⊥BC于E,如下图:
∵CD+BD=BC,CD=2BD,
∴2BD+BD=BC,
∴,
∵,
∴.
(3)连接BD,取BD的中点Q,连接AQ,CQ,如下图:
∵Q为BD的中点,
∴AQ是 △ ABD的中线,CQ是 △ CDB的中线,
∴,,
∴,
∴折线AQ-QC将四边形ABCD分成面积相等的两部分.
【分析】(1)由D是BC边上的中点,得AD是 △ABC的中线,,即可得到答案;
(2)作AE⊥BC于E,由CD+BD=BC,CD=2BD,得2BD+BD=BC,则,则可求出和,便可得到答案;
(3)连接BD,取BD的中点Q,连接AQ,CQ,则AQ是 △ ABD的中线,CQ是 △ CDB的中线,,,则,则可得到结论.
11.1 与三角形有关的线段本节综合检测题
一、填空题
1.已知三角形的三边分别为2,x,3,那么x的取值范围是
2.如图,在平面直角坐标系中,点A在x轴上,点B(0,9),线段AB向右平移3个单位至线段CD,线段CD与y轴交于点E,若图中阴影部分面积是21,则点C的坐标为 .
二、单选题
3.现有两根木棒,它们长分别是40cm和50cm,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10cm的木棒 B.40cm的木棒 C.90cm的木棒 D.100cm的木棒
4.若一个三角形的两边长分别为3cm和7cm,则第三边长可能是( )
A.4cm B.9cm C.10cm D.11cm
5.以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
6.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
7.下列各组数据表示三条线段的长。以各组线段为边,不能构成三角形的是( )
A.5,12,13 B.7,24,25 C.1,2,3 D.6,6,6
8.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间钱段最短
C.两点确定一条直线 D.垂线段最短
9.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
10.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
11.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是( )
A.1cm B.2cm C.3cm D.5cm
12.如图,点D和点E分别是△ABC边BC和AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为12,则△BDF与△AEF的面积之差为( )
A.1 B.1.5 C.1.75 D.2
三、解答题
13.如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(﹣1,3),B(﹣3,2),C(﹣4,0),D(0,0),求四边形ABCD的面积.
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积
16.已知三角形的三边互不相等,且有两边长分别为5和7,第三边长为正整数.
①请写出一个三角形符合上述条件的第三边长.
②若符合上述条件的三角形共有n个,求n的值.
③试求出②中这n个三角形的周长为偶数的三角形所占的比例.
四、计算题
17.已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
五、综合题
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求:
(1)∠BCD的度数;
(2)∠ECD的度数.
19.如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.在平面直角坐标系 中,对于点 ,若点 的坐标为 ,则称点是的“ 演化点”.例如,点 的“ 演化点”为 ,即 .
(1)已知点 的“ 演化点”是 ,则 的坐标为 ;
(2)已知点 ,且点 的“ 演化点”是 ,则 的面积 为 ;
(3)已知 , , , ,且点 的“ 演化点”为 ,当 时, .
六、实践探究题
21.阅读材料;若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴m=4,n=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0.则2x+3y的值为 ;
(2)已知△ABC的边长a、b、c是三个互不相等的正整数,且满足a2+b2﹣4a﹣6b+13=0,求c的值;(写出求解过程)
(3)已知a﹣b=10,ab+c2﹣16c+89=0,则a+b+c的值为 .
22.综合与实践
【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点是BC边上的中点,连接AD.求证:.
证明:过点作于
(1)【拓展探究】
如图2,在△ABC中,点D是BC边上的中点中,点是BC边上的中点,若,则 .
(2)如图3,在中,点是BC边上的点且和存在怎样的数量关系 请模仿写出证明过程.
(3)【问题解决】
现在有一块四边形土地ABCD(如图4),能大和都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
答案解析部分
1.【答案】1<x<5
【解析】【解答】解:由题意得:3-2<x<3+2,
即1<x<5.
故答案为:1<x<5.
【分析】根据三角形三边关系(两边之和大于第三边,两边之差小于第三边)列出不等式组,解这个不等式组即可.
2.【答案】
【解析】【解答】解:连接BC,AE,设OE=x,OC=y.
∵CE∥AB,
∴S△ACB=S△ABE,
∴×3×9=×(9 x)×(3+y) ①,
又∵×(3+y)×9 xy=21 ②,
联立①与②得x=5,y=,
∴C点坐标为.
故答案为:.
【分析】连接BC,AE,设OE=x,OC=y.根据平移的性质得AB∥CD,再根据等底同高的三角形的面积相等得S△ACB=S△ABE,进而根据三角面积计算方法建立方程组,求解即可.
3.【答案】B
【解析】【解答】已知三角形的两边是40cm和50cm,则
10<第三边<90.
故答案为:40cm的木棒.
故答案为:B.
【分析】利用三角形三边的关系可得10<第三边<90,再求解即可。
4.【答案】B
【解析】【解答】解:设第三边长为x cm,根据三角形的三边关系可得:7-3<x<7+3,
解得:4<x<10,
∴第三边长可能是9cm.
故答案为:B.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边长的范围,然后结合各个选项中的数据进行判断.
5.【答案】B
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
6.【答案】B
【解析】【解答】解: ①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故答案为:B.
【分析】根据三角形的三条中线,三条角平分线,三条高的位置判断.
三角形的三条中线都在三角形内部;
三角形的三条角平分线都在三角形内部;
三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上.
7.【答案】C
【解析】【分析】三角形的基本关系满足,两边之和大于第三边,两边之差小于第三边,本题中唯一不能构成三角形的是C,不满足三角形的三边的基本关系,故选C.
【点评】本题属于对三角形的三边的基本关系的理解和运用。
8.【答案】A
【解析】【解答】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.故答案为:A
【分析】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.
9.【答案】C
【解析】【解答】解:线段BE是△ABC的高的图是选项C.
故答案为:C.
【分析】根据高的定义对每个选项一一判断求解即可。
10.【答案】C
【解析】【解答】解:∵L1∥L2,
∴L1,L2之间的距离是固定的,
∴△ABC和△DBC的BC边上的高相等,
∴△ABC和△DBC的面积相等,
∴△DBC的面积等于10.
故选C.
【分析】由于平行线间的距离处处相等,而△ABC和△DBC的BC边上的高相等,所以△ABC和△DBC的面积相等,即可求出答案.
11.【答案】B
【解析】【解答】解:
∵BD是△ABC的中线,
∴AD=CD,
∵△ABD周长=AB+AD+BD,△BCD周长=BC+CD+BD,
∴△ABD周长﹣△BCD周长=(AB+AD+BD)﹣(BC+CD+BD)=AB﹣BC=5﹣3=2(cm),
即△ABD和△BCD的周长之差是2cm,
故选B.
【分析】利用中线的定义可知AD=CD,可知△ABD和△BCD的周长之差即为AB和BC的差,可求得答案.
12.【答案】D
【解析】【解答】解:设BC边的高为hBC,AC边的高为hAC,
∵S△ABC=BC hBC=AC hAC=12,
∴S△ABC=(BD+CD) hBC=(AE+CE) hAC=12,
∵AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,
∴S△AEB=S△CEB=S△ABC=×12=6,
即S△AEF+S△ABF=6①,
∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD hBC,
∴S△ABD=S△ABC=×12=8,
即S△BDF+S△ABF=8②,
②﹣①得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=8﹣6=2,
故答案为:D.
【分析】设BC边的高为hBC,AC边的高为hAC,根据S△ABC=BC hBC,得出S△ABC=12,根据AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,S△AEB=6,即S△AEF+S△ABF=6①,再得出S△ABD=8,即S△BDF+S△ABF=8②,利用②﹣①即可得解。
13.【答案】解:四边形ABCD的面积= ×1×2+ ×(2+3)×2+ ×1×3=1+5+1.5=7.5.
故四边形ABCD的面积为7.5
【解析】【分析】把四边形ABCD分成两个直角三角形和一个直角梯形,然后根据点的坐标和三角形面积公式与梯形面积公式进行计算即可.
14.【答案】解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
【解析】【分析】根据三角形中线的定义得出BD = CD, 再根据△ABD和△ADC的周长差是4cm列出等式,化简得出AB – AC = 4cm, 即可求出AC的长.
15.【答案】解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
故答案为:8.
【解析】【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
16.【答案】【解答】两边长分别为5和7,设第三边是a,则7-5<a<7+5,即2<a<12.①第三边长是3.(答案不唯一);②∵2<a<12,∴n=7;③周长为偶数的三角形个数是4,周长为偶数的三角形所占的比例为4:7.
【解析】【分析】①根据三角形三边关系求得第三边的取值范围,即可求解;
②找到第三边的取值范围内的正整数的个数,即为所求;
③用周长为偶数的三角形个数÷三角形的总个数,列式计算即可求解.
17.【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
18.【答案】(1)解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°
(2)解:∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=50°-30°=20°
【解析】【分析】(1)根据垂直的定义得出 ∠CDB=90°, 根据直角三角形的两锐角互余得出 ∠BCD=90°-∠B=30° ;
(2)根据三角形的内角和得出 ∠ACB=100°, 根据角平分线的定义得出 ∠BCE= ∠ACB=50°, 最后根据角的和差,由 ∠ECD=∠BCE-∠BCD 算出答案。
19.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)
(2)解:标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为= ×5×4=10
【解析】【分析】(1)根据学校的位置可建立直角坐标系,进而写出图书馆B位置的坐标;
(2)根据C的坐标可得体育馆的位置,然后连接A、B、C,接下来根据三角形的面积公式计算即可.
20.【答案】(1)(2,14)
(2)20
(3)
【解析】【解答】解:(1)由题意可知:点 的“ 演化点”是 ,即 ,
故答案为:(2,14);
( 2 )设Q点坐标为(x,y),由题意可知: ,解得:
∴Q点坐标为(0,4)
∴
故答案为:20;
( 3 )由题意可知:AD=3,OC=5
的坐标为 ,即点 的坐标为
当点 位于y轴正半轴时, ,
∴ 或 (此情况不合题意,舍去)
又∵
∴ ,解得: (舍去)
当点 位于y轴正半轴时, ,
∴
又∵
∴ ,解得: ,即
故答案为: .
【分析】(1)根据题意a=3,x=-1,y=5时,求点 的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出 ,然后分点 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
21.【答案】(1)-1
(2)解:∵a2+b2﹣4a﹣6b+13=a2﹣4a+4+b2﹣6b+9=(a﹣2)2+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
∴a=2,b=3,
∵a、b、c是△ABC的三边,
∴1<c<5,
∵a、b、c是三个互不相等的正整数,
∴c=4;
(3)8
【解析】【解答】解:(1)∵x2+2xy+2y2+2y+1=x2+2xy+y2+y2+2y+1=(x+y)2+(y+1)2=0,
∴(x+y)2=0,(y+1)2=0,
∴y=﹣1,x=1,
∴2x+3y=2×1+3×(-1)=﹣1;
(3)∵a﹣b=10,即a=b+10,代入得:b(b+10)+c2﹣16c+89=0,
整理得:(b2+10b+25)+(c2﹣16c+64)=(b+5)2+(c﹣8)2=0,
∴b+5=0,c﹣8=0,
解得b=﹣5,c=8,
则a=5,
则a+b+c=5﹣5+8=8.
【分析】(1)对已知等式进行变形可得(x+y)2+(y+1)2=0,根据偶次幂的非负性可得x+y=0、y+1=0,求出x、y的值,然后代入2x+3y中进行计算;
(2)对已知等式进行变形可得(a-2)2+(b-3)2=0,根据偶次幂的非负性可得a-2=0、b-3=0,求出a、b的值,结合三角形的三边关系求出c的范围,根据a、b、c是三个互不相等的正整数就可得到c的值;
(3)由已知条件可得a=b+10,代入等式中并整理可得(b+5)2+(c-8)2=0,根据偶次幂的非负性可得b+5=0,c﹣8=0,求出a、b、c的值,然后根据有理数的加法法则进行计算.
22.【答案】(1)3
(2);理由如下:
过点A作AE⊥BC于E
∵CD=2BD
∴AC=3BD
∴
(3)方法一:如图,连接BD,取BD的中点,连接AE,BE,则四边形ADEC就是四边形ABCD的一半。
方法二:如图,取AD的中点H、取BC的中点F,连接AF,CH,则四边形AFCH就是四边形ABCD的一半。
【解析】【解答】解:(1)∵点D是BC边上的中点,
∴AD是 △ ABC的中线,
∴,
∵,
∴,
故答案为:3.
(2),
理由如下:作AE⊥BC于E,如下图:
∵CD+BD=BC,CD=2BD,
∴2BD+BD=BC,
∴,
∵,
∴.
(3)连接BD,取BD的中点Q,连接AQ,CQ,如下图:
∵Q为BD的中点,
∴AQ是 △ ABD的中线,CQ是 △ CDB的中线,
∴,,
∴,
∴折线AQ-QC将四边形ABCD分成面积相等的两部分.
【分析】(1)由D是BC边上的中点,得AD是 △ABC的中线,,即可得到答案;
(2)作AE⊥BC于E,由CD+BD=BC,CD=2BD,得2BD+BD=BC,则,则可求出和,便可得到答案;
(3)连接BD,取BD的中点Q,连接AQ,CQ,则AQ是 △ ABD的中线,CQ是 △ CDB的中线,,,则,则可得到结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.1 与三角形有关的线段本节综合检测题
一、填空题
1.已知三角形的三边分别为2,x,3,那么x的取值范围是
2.如图,在平面直角坐标系中,点A在x轴上,点B(0,9),线段AB向右平移3个单位至线段CD,线段CD与y轴交于点E,若图中阴影部分面积是21,则点C的坐标为 .
二、单选题
3.现有两根木棒,它们长分别是40cm和50cm,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10cm的木棒 B.40cm的木棒 C.90cm的木棒 D.100cm的木棒
4.若一个三角形的两边长分别为3cm和7cm,则第三边长可能是( )
A.4cm B.9cm C.10cm D.11cm
5.以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
6.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
7.下列各组数据表示三条线段的长。以各组线段为边,不能构成三角形的是( )
A.5,12,13 B.7,24,25 C.1,2,3 D.6,6,6
8.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间钱段最短
C.两点确定一条直线 D.垂线段最短
9.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
10.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
11.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是( )
A.1cm B.2cm C.3cm D.5cm
12.如图,点D和点E分别是△ABC边BC和AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为12,则△BDF与△AEF的面积之差为( )
A.1 B.1.5 C.1.75 D.2
三、解答题
13.如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(﹣1,3),B(﹣3,2),C(﹣4,0),D(0,0),求四边形ABCD的面积.
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积
16.已知三角形的三边互不相等,且有两边长分别为5和7,第三边长为正整数.
①请写出一个三角形符合上述条件的第三边长.
②若符合上述条件的三角形共有n个,求n的值.
③试求出②中这n个三角形的周长为偶数的三角形所占的比例.
四、计算题
17.已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
五、综合题
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求:
(1)∠BCD的度数;
(2)∠ECD的度数.
19.如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.在平面直角坐标系 中,对于点 ,若点 的坐标为 ,则称点是的“ 演化点”.例如,点 的“ 演化点”为 ,即 .
(1)已知点 的“ 演化点”是 ,则 的坐标为 ;
(2)已知点 ,且点 的“ 演化点”是 ,则 的面积 为 ;
(3)已知 , , , ,且点 的“ 演化点”为 ,当 时, .
六、实践探究题
21.阅读材料;若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴m=4,n=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0.则2x+3y的值为 ;
(2)已知△ABC的边长a、b、c是三个互不相等的正整数,且满足a2+b2﹣4a﹣6b+13=0,求c的值;(写出求解过程)
(3)已知a﹣b=10,ab+c2﹣16c+89=0,则a+b+c的值为 .
22.综合与实践
【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点是BC边上的中点,连接AD.求证:.
证明:过点作于
(1)【拓展探究】
如图2,在△ABC中,点D是BC边上的中点中,点是BC边上的中点,若,则 .
(2)如图3,在中,点是BC边上的点且和存在怎样的数量关系 请模仿写出证明过程.
(3)【问题解决】
现在有一块四边形土地ABCD(如图4),能大和都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
答案解析部分
1.【答案】1<x<5
【解析】【解答】解:由题意得:3-2<x<3+2,
即1<x<5.
故答案为:1<x<5.
【分析】根据三角形三边关系(两边之和大于第三边,两边之差小于第三边)列出不等式组,解这个不等式组即可.
2.【答案】
【解析】【解答】解:连接BC,AE,设OE=x,OC=y.
∵CE∥AB,
∴S△ACB=S△ABE,
∴×3×9=×(9 x)×(3+y) ①,
又∵×(3+y)×9 xy=21 ②,
联立①与②得x=5,y=,
∴C点坐标为.
故答案为:.
【分析】连接BC,AE,设OE=x,OC=y.根据平移的性质得AB∥CD,再根据等底同高的三角形的面积相等得S△ACB=S△ABE,进而根据三角面积计算方法建立方程组,求解即可.
3.【答案】B
【解析】【解答】已知三角形的两边是40cm和50cm,则
10<第三边<90.
故答案为:40cm的木棒.
故答案为:B.
【分析】利用三角形三边的关系可得10<第三边<90,再求解即可。
4.【答案】B
【解析】【解答】解:设第三边长为x cm,根据三角形的三边关系可得:7-3<x<7+3,
解得:4<x<10,
∴第三边长可能是9cm.
故答案为:B.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边长的范围,然后结合各个选项中的数据进行判断.
5.【答案】B
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
6.【答案】B
【解析】【解答】解: ①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故答案为:B.
【分析】根据三角形的三条中线,三条角平分线,三条高的位置判断.
三角形的三条中线都在三角形内部;
三角形的三条角平分线都在三角形内部;
三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上.
7.【答案】C
【解析】【分析】三角形的基本关系满足,两边之和大于第三边,两边之差小于第三边,本题中唯一不能构成三角形的是C,不满足三角形的三边的基本关系,故选C.
【点评】本题属于对三角形的三边的基本关系的理解和运用。
8.【答案】A
【解析】【解答】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.故答案为:A
【分析】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.
9.【答案】C
【解析】【解答】解:线段BE是△ABC的高的图是选项C.
故答案为:C.
【分析】根据高的定义对每个选项一一判断求解即可。
10.【答案】C
【解析】【解答】解:∵L1∥L2,
∴L1,L2之间的距离是固定的,
∴△ABC和△DBC的BC边上的高相等,
∴△ABC和△DBC的面积相等,
∴△DBC的面积等于10.
故选C.
【分析】由于平行线间的距离处处相等,而△ABC和△DBC的BC边上的高相等,所以△ABC和△DBC的面积相等,即可求出答案.
11.【答案】B
【解析】【解答】解:
∵BD是△ABC的中线,
∴AD=CD,
∵△ABD周长=AB+AD+BD,△BCD周长=BC+CD+BD,
∴△ABD周长﹣△BCD周长=(AB+AD+BD)﹣(BC+CD+BD)=AB﹣BC=5﹣3=2(cm),
即△ABD和△BCD的周长之差是2cm,
故选B.
【分析】利用中线的定义可知AD=CD,可知△ABD和△BCD的周长之差即为AB和BC的差,可求得答案.
12.【答案】D
【解析】【解答】解:设BC边的高为hBC,AC边的高为hAC,
∵S△ABC=BC hBC=AC hAC=12,
∴S△ABC=(BD+CD) hBC=(AE+CE) hAC=12,
∵AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,
∴S△AEB=S△CEB=S△ABC=×12=6,
即S△AEF+S△ABF=6①,
∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD hBC,
∴S△ABD=S△ABC=×12=8,
即S△BDF+S△ABF=8②,
②﹣①得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=8﹣6=2,
故答案为:D.
【分析】设BC边的高为hBC,AC边的高为hAC,根据S△ABC=BC hBC,得出S△ABC=12,根据AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,S△AEB=6,即S△AEF+S△ABF=6①,再得出S△ABD=8,即S△BDF+S△ABF=8②,利用②﹣①即可得解。
13.【答案】解:四边形ABCD的面积= ×1×2+ ×(2+3)×2+ ×1×3=1+5+1.5=7.5.
故四边形ABCD的面积为7.5
【解析】【分析】把四边形ABCD分成两个直角三角形和一个直角梯形,然后根据点的坐标和三角形面积公式与梯形面积公式进行计算即可.
14.【答案】解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
【解析】【分析】根据三角形中线的定义得出BD = CD, 再根据△ABD和△ADC的周长差是4cm列出等式,化简得出AB – AC = 4cm, 即可求出AC的长.
15.【答案】解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
故答案为:8.
【解析】【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
16.【答案】【解答】两边长分别为5和7,设第三边是a,则7-5<a<7+5,即2<a<12.①第三边长是3.(答案不唯一);②∵2<a<12,∴n=7;③周长为偶数的三角形个数是4,周长为偶数的三角形所占的比例为4:7.
【解析】【分析】①根据三角形三边关系求得第三边的取值范围,即可求解;
②找到第三边的取值范围内的正整数的个数,即为所求;
③用周长为偶数的三角形个数÷三角形的总个数,列式计算即可求解.
17.【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
18.【答案】(1)解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°
(2)解:∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=50°-30°=20°
【解析】【分析】(1)根据垂直的定义得出 ∠CDB=90°, 根据直角三角形的两锐角互余得出 ∠BCD=90°-∠B=30° ;
(2)根据三角形的内角和得出 ∠ACB=100°, 根据角平分线的定义得出 ∠BCE= ∠ACB=50°, 最后根据角的和差,由 ∠ECD=∠BCE-∠BCD 算出答案。
19.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)
(2)解:标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为= ×5×4=10
【解析】【分析】(1)根据学校的位置可建立直角坐标系,进而写出图书馆B位置的坐标;
(2)根据C的坐标可得体育馆的位置,然后连接A、B、C,接下来根据三角形的面积公式计算即可.
20.【答案】(1)(2,14)
(2)20
(3)
【解析】【解答】解:(1)由题意可知:点 的“ 演化点”是 ,即 ,
故答案为:(2,14);
( 2 )设Q点坐标为(x,y),由题意可知: ,解得:
∴Q点坐标为(0,4)
∴
故答案为:20;
( 3 )由题意可知:AD=3,OC=5
的坐标为 ,即点 的坐标为
当点 位于y轴正半轴时, ,
∴ 或 (此情况不合题意,舍去)
又∵
∴ ,解得: (舍去)
当点 位于y轴正半轴时, ,
∴
又∵
∴ ,解得: ,即
故答案为: .
【分析】(1)根据题意a=3,x=-1,y=5时,求点 的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出 ,然后分点 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
21.【答案】(1)-1
(2)解:∵a2+b2﹣4a﹣6b+13=a2﹣4a+4+b2﹣6b+9=(a﹣2)2+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
∴a=2,b=3,
∵a、b、c是△ABC的三边,
∴1<c<5,
∵a、b、c是三个互不相等的正整数,
∴c=4;
(3)8
【解析】【解答】解:(1)∵x2+2xy+2y2+2y+1=x2+2xy+y2+y2+2y+1=(x+y)2+(y+1)2=0,
∴(x+y)2=0,(y+1)2=0,
∴y=﹣1,x=1,
∴2x+3y=2×1+3×(-1)=﹣1;
(3)∵a﹣b=10,即a=b+10,代入得:b(b+10)+c2﹣16c+89=0,
整理得:(b2+10b+25)+(c2﹣16c+64)=(b+5)2+(c﹣8)2=0,
∴b+5=0,c﹣8=0,
解得b=﹣5,c=8,
则a=5,
则a+b+c=5﹣5+8=8.
【分析】(1)对已知等式进行变形可得(x+y)2+(y+1)2=0,根据偶次幂的非负性可得x+y=0、y+1=0,求出x、y的值,然后代入2x+3y中进行计算;
(2)对已知等式进行变形可得(a-2)2+(b-3)2=0,根据偶次幂的非负性可得a-2=0、b-3=0,求出a、b的值,结合三角形的三边关系求出c的范围,根据a、b、c是三个互不相等的正整数就可得到c的值;
(3)由已知条件可得a=b+10,代入等式中并整理可得(b+5)2+(c-8)2=0,根据偶次幂的非负性可得b+5=0,c﹣8=0,求出a、b、c的值,然后根据有理数的加法法则进行计算.
22.【答案】(1)3
(2);理由如下:
过点A作AE⊥BC于E
∵CD=2BD
∴AC=3BD
∴
(3)方法一:如图,连接BD,取BD的中点,连接AE,BE,则四边形ADEC就是四边形ABCD的一半。
方法二:如图,取AD的中点H、取BC的中点F,连接AF,CH,则四边形AFCH就是四边形ABCD的一半。
【解析】【解答】解:(1)∵点D是BC边上的中点,
∴AD是 △ ABC的中线,
∴,
∵,
∴,
故答案为:3.
(2),
理由如下:作AE⊥BC于E,如下图:
∵CD+BD=BC,CD=2BD,
∴2BD+BD=BC,
∴,
∵,
∴.
(3)连接BD,取BD的中点Q,连接AQ,CQ,如下图:
∵Q为BD的中点,
∴AQ是 △ ABD的中线,CQ是 △ CDB的中线,
∴,,
∴,
∴折线AQ-QC将四边形ABCD分成面积相等的两部分.
【分析】(1)由D是BC边上的中点,得AD是 △ABC的中线,,即可得到答案;
(2)作AE⊥BC于E,由CD+BD=BC,CD=2BD,得2BD+BD=BC,则,则可求出和,便可得到答案;
(3)连接BD,取BD的中点Q,连接AQ,CQ,则AQ是 △ ABD的中线,CQ是 △ CDB的中线,,,则,则可得到结论.
11.1 与三角形有关的线段本节综合检测题
一、填空题
1.已知三角形的三边分别为2,x,3,那么x的取值范围是
2.如图,在平面直角坐标系中,点A在x轴上,点B(0,9),线段AB向右平移3个单位至线段CD,线段CD与y轴交于点E,若图中阴影部分面积是21,则点C的坐标为 .
二、单选题
3.现有两根木棒,它们长分别是40cm和50cm,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10cm的木棒 B.40cm的木棒 C.90cm的木棒 D.100cm的木棒
4.若一个三角形的两边长分别为3cm和7cm,则第三边长可能是( )
A.4cm B.9cm C.10cm D.11cm
5.以下各组线段为边,能组成三角形的是( )
A.2cm,4cm,6cm B.8cm,6cm,4cm
C.14cm,6cm,7cm D.2cm,3cm,6cm
6.下列说法正确的是( )
①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角形三条高都在三角形的内部.
A.①②③ B.①② C.②③ D.①③
7.下列各组数据表示三条线段的长。以各组线段为边,不能构成三角形的是( )
A.5,12,13 B.7,24,25 C.1,2,3 D.6,6,6
8.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.三角形的稳定性 B.两点之间钱段最短
C.两点确定一条直线 D.垂线段最短
9.下列四个图形中,线段BE表示△ABC的高的是( )
A. B.
C. D.
10.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
11.BD是△ABC的中线,若AB=5cm,BC=3cm,则△ABD与△BCD的周长之差是( )
A.1cm B.2cm C.3cm D.5cm
12.如图,点D和点E分别是△ABC边BC和AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为12,则△BDF与△AEF的面积之差为( )
A.1 B.1.5 C.1.75 D.2
三、解答题
13.如图所示的直角坐标系中,四边形ABCD各个顶点的坐标分别为A(﹣1,3),B(﹣3,2),C(﹣4,0),D(0,0),求四边形ABCD的面积.
14.如图,AD为△ABC的中线,AB = 12cm,△ABD和△ADC的周长差是4cm,求△ABC的边AC的长(AC AB).
15.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.
(1)补全△A′B′C′根据下列条件,利用网格点和三角板画图:
(2)画出AB边上的中线CD;
(3)画出BC边上的高线AE;
(4)△A′B′C′的面积
16.已知三角形的三边互不相等,且有两边长分别为5和7,第三边长为正整数.
①请写出一个三角形符合上述条件的第三边长.
②若符合上述条件的三角形共有n个,求n的值.
③试求出②中这n个三角形的周长为偶数的三角形所占的比例.
四、计算题
17.已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
五、综合题
18.在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°,求:
(1)∠BCD的度数;
(2)∠ECD的度数.
19.如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
20.在平面直角坐标系 中,对于点 ,若点 的坐标为 ,则称点是的“ 演化点”.例如,点 的“ 演化点”为 ,即 .
(1)已知点 的“ 演化点”是 ,则 的坐标为 ;
(2)已知点 ,且点 的“ 演化点”是 ,则 的面积 为 ;
(3)已知 , , , ,且点 的“ 演化点”为 ,当 时, .
六、实践探究题
21.阅读材料;若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴m=4,n=4.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0.则2x+3y的值为 ;
(2)已知△ABC的边长a、b、c是三个互不相等的正整数,且满足a2+b2﹣4a﹣6b+13=0,求c的值;(写出求解过程)
(3)已知a﹣b=10,ab+c2﹣16c+89=0,则a+b+c的值为 .
22.综合与实践
【知识生成】三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点是BC边上的中点,连接AD.求证:.
证明:过点作于
(1)【拓展探究】
如图2,在△ABC中,点D是BC边上的中点中,点是BC边上的中点,若,则 .
(2)如图3,在中,点是BC边上的点且和存在怎样的数量关系 请模仿写出证明过程.
(3)【问题解决】
现在有一块四边形土地ABCD(如图4),能大和都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
要求:用不超过三条的线段画出平分方法,并对作法进行描述.可利用带刻度的直尺.
答案解析部分
1.【答案】1<x<5
【解析】【解答】解:由题意得:3-2<x<3+2,
即1<x<5.
故答案为:1<x<5.
【分析】根据三角形三边关系(两边之和大于第三边,两边之差小于第三边)列出不等式组,解这个不等式组即可.
2.【答案】
【解析】【解答】解:连接BC,AE,设OE=x,OC=y.
∵CE∥AB,
∴S△ACB=S△ABE,
∴×3×9=×(9 x)×(3+y) ①,
又∵×(3+y)×9 xy=21 ②,
联立①与②得x=5,y=,
∴C点坐标为.
故答案为:.
【分析】连接BC,AE,设OE=x,OC=y.根据平移的性质得AB∥CD,再根据等底同高的三角形的面积相等得S△ACB=S△ABE,进而根据三角面积计算方法建立方程组,求解即可.
3.【答案】B
【解析】【解答】已知三角形的两边是40cm和50cm,则
10<第三边<90.
故答案为:40cm的木棒.
故答案为:B.
【分析】利用三角形三边的关系可得10<第三边<90,再求解即可。
4.【答案】B
【解析】【解答】解:设第三边长为x cm,根据三角形的三边关系可得:7-3<x<7+3,
解得:4<x<10,
∴第三边长可能是9cm.
故答案为:B.
【分析】三角形的三边关系:任意两边之差小于第三边,任意两边之和大于第三边,据此求出第三边长的范围,然后结合各个选项中的数据进行判断.
5.【答案】B
【解析】【解答】解:A、2+4=6,不能组成三角形;
B、4+6=10>8,能组成三角形;
C、6+7=13<14,不能够组成三角形;
D、2+3=5<6,不能组成三角形.
故选B.
【分析】根据三角形任意两边的和大于第三边,进行分析判断.
6.【答案】B
【解析】【解答】解: ①、②正确;
而对于三角形三条高:
锐角三角形的三条高在三角形的内部;
直角三角形有两条高在边上;
钝角三角形有两条高在外部,故③错误.
故答案为:B.
【分析】根据三角形的三条中线,三条角平分线,三条高的位置判断.
三角形的三条中线都在三角形内部;
三角形的三条角平分线都在三角形内部;
三角形三条高可以在内部,也可以在外部,直角三角形有两条高在边上.
7.【答案】C
【解析】【分析】三角形的基本关系满足,两边之和大于第三边,两边之差小于第三边,本题中唯一不能构成三角形的是C,不满足三角形的三边的基本关系,故选C.
【点评】本题属于对三角形的三边的基本关系的理解和运用。
8.【答案】A
【解析】【解答】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.故答案为:A
【分析】窗户打开后,用窗钩钩住,正好构成三角形的形状,因此可以将其固定,主要利用了三角形的稳定性.
9.【答案】C
【解析】【解答】解:线段BE是△ABC的高的图是选项C.
故答案为:C.
【分析】根据高的定义对每个选项一一判断求解即可。
10.【答案】C
【解析】【解答】解:∵L1∥L2,
∴L1,L2之间的距离是固定的,
∴△ABC和△DBC的BC边上的高相等,
∴△ABC和△DBC的面积相等,
∴△DBC的面积等于10.
故选C.
【分析】由于平行线间的距离处处相等,而△ABC和△DBC的BC边上的高相等,所以△ABC和△DBC的面积相等,即可求出答案.
11.【答案】B
【解析】【解答】解:
∵BD是△ABC的中线,
∴AD=CD,
∵△ABD周长=AB+AD+BD,△BCD周长=BC+CD+BD,
∴△ABD周长﹣△BCD周长=(AB+AD+BD)﹣(BC+CD+BD)=AB﹣BC=5﹣3=2(cm),
即△ABD和△BCD的周长之差是2cm,
故选B.
【分析】利用中线的定义可知AD=CD,可知△ABD和△BCD的周长之差即为AB和BC的差,可求得答案.
12.【答案】D
【解析】【解答】解:设BC边的高为hBC,AC边的高为hAC,
∵S△ABC=BC hBC=AC hAC=12,
∴S△ABC=(BD+CD) hBC=(AE+CE) hAC=12,
∵AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,
∴S△AEB=S△CEB=S△ABC=×12=6,
即S△AEF+S△ABF=6①,
∵BD=2CD,BD+CD=BC,
∴BD=BC,S△ABD=BD hBC,
∴S△ABD=S△ABC=×12=8,
即S△BDF+S△ABF=8②,
②﹣①得:S△BDF﹣SAEF=(S△BDF+S△ABF)﹣(S△AEF+S△ABF)=8﹣6=2,
故答案为:D.
【分析】设BC边的高为hBC,AC边的高为hAC,根据S△ABC=BC hBC,得出S△ABC=12,根据AE=CE,S△AEB=AE hAC,S△BCE=EC hAC,S△AEB=6,即S△AEF+S△ABF=6①,再得出S△ABD=8,即S△BDF+S△ABF=8②,利用②﹣①即可得解。
13.【答案】解:四边形ABCD的面积= ×1×2+ ×(2+3)×2+ ×1×3=1+5+1.5=7.5.
故四边形ABCD的面积为7.5
【解析】【分析】把四边形ABCD分成两个直角三角形和一个直角梯形,然后根据点的坐标和三角形面积公式与梯形面积公式进行计算即可.
14.【答案】解:∵AD为△ABC的中线,
∴BD = CD,
∵△ABD和△ADC的周长差是4cm,
∴AB + AD + BD – (AC + AD + CD) = AB + AD + BD – AC – AD – BD = AB – AC = 4cm,
∵AB = 12cm,
∴AC = AB – 4cm = 8cm.
【解析】【分析】根据三角形中线的定义得出BD = CD, 再根据△ABD和△ADC的周长差是4cm列出等式,化简得出AB – AC = 4cm, 即可求出AC的长.
15.【答案】解:(1)如图所示:△A′B′C′即为所求;
(2)如图所示:CD就是所求的中线;
(3)如图所示:AE即为BC边上的高;
(4)4×4÷2=16÷2=8.
故△A′B′C′的面积为8.
故答案为:8.
【解析】【分析】(1)连接BB′,过A、C分别做BB′的平行线,并且在平行线上截取AA′=CC′=BB′,顺次连接平移后各点,得到的三角形即为平移后的三角形;
(2)作AB的垂直平分线找到中点D,连接CD,CD就是所求的中线.
(3)从A点向BC的延长线作垂线,垂足为点E,AE即为BC边上的高;
(4)根据三角形面积公式即可求出△A′B′C′的面积.
16.【答案】【解答】两边长分别为5和7,设第三边是a,则7-5<a<7+5,即2<a<12.①第三边长是3.(答案不唯一);②∵2<a<12,∴n=7;③周长为偶数的三角形个数是4,周长为偶数的三角形所占的比例为4:7.
【解析】【分析】①根据三角形三边关系求得第三边的取值范围,即可求解;
②找到第三边的取值范围内的正整数的个数,即为所求;
③用周长为偶数的三角形个数÷三角形的总个数,列式计算即可求解.
17.【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
18.【答案】(1)解:∵CD⊥AB,
∴∠CDB=90°,
∵∠B=60°,
∴∠BCD=90°-∠B=90°-60°=30°
(2)解:∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,
∴∠ACB=100°,
∵CE是∠ACB的平分线,
∴∠BCE= ∠ACB=50°,
∴∠ECD=∠BCE-∠BCD=50°-30°=20°
【解析】【分析】(1)根据垂直的定义得出 ∠CDB=90°, 根据直角三角形的两锐角互余得出 ∠BCD=90°-∠B=30° ;
(2)根据三角形的内角和得出 ∠ACB=100°, 根据角平分线的定义得出 ∠BCE= ∠ACB=50°, 最后根据角的和差,由 ∠ECD=∠BCE-∠BCD 算出答案。
19.【答案】(1)解:建立直角坐标系如图所示:
图书馆B位置的坐标为(-3,-2)
(2)解:标出体育馆位置C如图所示,观察可得,△ABC中BC边长为5,BC边上的高为4,所以△ABC的面积为= ×5×4=10
【解析】【分析】(1)根据学校的位置可建立直角坐标系,进而写出图书馆B位置的坐标;
(2)根据C的坐标可得体育馆的位置,然后连接A、B、C,接下来根据三角形的面积公式计算即可.
20.【答案】(1)(2,14)
(2)20
(3)
【解析】【解答】解:(1)由题意可知:点 的“ 演化点”是 ,即 ,
故答案为:(2,14);
( 2 )设Q点坐标为(x,y),由题意可知: ,解得:
∴Q点坐标为(0,4)
∴
故答案为:20;
( 3 )由题意可知:AD=3,OC=5
的坐标为 ,即点 的坐标为
当点 位于y轴正半轴时, ,
∴ 或 (此情况不合题意,舍去)
又∵
∴ ,解得: (舍去)
当点 位于y轴正半轴时, ,
∴
又∵
∴ ,解得: ,即
故答案为: .
【分析】(1)根据题意a=3,x=-1,y=5时,求点 的坐标;
(2)根据题意列方程组求点Q的坐标,然后结合坐标系中点的位置,利用割补法求三角形面积;
(3)根据题意求出 ,然后分点 在y轴正半轴和负半轴两种情况讨论,利用三角形面积列方程求解.
21.【答案】(1)-1
(2)解:∵a2+b2﹣4a﹣6b+13=a2﹣4a+4+b2﹣6b+9=(a﹣2)2+(b﹣3)2=0,
∴a﹣2=0,b﹣3=0,
∴a=2,b=3,
∵a、b、c是△ABC的三边,
∴1<c<5,
∵a、b、c是三个互不相等的正整数,
∴c=4;
(3)8
【解析】【解答】解:(1)∵x2+2xy+2y2+2y+1=x2+2xy+y2+y2+2y+1=(x+y)2+(y+1)2=0,
∴(x+y)2=0,(y+1)2=0,
∴y=﹣1,x=1,
∴2x+3y=2×1+3×(-1)=﹣1;
(3)∵a﹣b=10,即a=b+10,代入得:b(b+10)+c2﹣16c+89=0,
整理得:(b2+10b+25)+(c2﹣16c+64)=(b+5)2+(c﹣8)2=0,
∴b+5=0,c﹣8=0,
解得b=﹣5,c=8,
则a=5,
则a+b+c=5﹣5+8=8.
【分析】(1)对已知等式进行变形可得(x+y)2+(y+1)2=0,根据偶次幂的非负性可得x+y=0、y+1=0,求出x、y的值,然后代入2x+3y中进行计算;
(2)对已知等式进行变形可得(a-2)2+(b-3)2=0,根据偶次幂的非负性可得a-2=0、b-3=0,求出a、b的值,结合三角形的三边关系求出c的范围,根据a、b、c是三个互不相等的正整数就可得到c的值;
(3)由已知条件可得a=b+10,代入等式中并整理可得(b+5)2+(c-8)2=0,根据偶次幂的非负性可得b+5=0,c﹣8=0,求出a、b、c的值,然后根据有理数的加法法则进行计算.
22.【答案】(1)3
(2);理由如下:
过点A作AE⊥BC于E
∵CD=2BD
∴AC=3BD
∴
(3)方法一:如图,连接BD,取BD的中点,连接AE,BE,则四边形ADEC就是四边形ABCD的一半。
方法二:如图,取AD的中点H、取BC的中点F,连接AF,CH,则四边形AFCH就是四边形ABCD的一半。
【解析】【解答】解:(1)∵点D是BC边上的中点,
∴AD是 △ ABC的中线,
∴,
∵,
∴,
故答案为:3.
(2),
理由如下:作AE⊥BC于E,如下图:
∵CD+BD=BC,CD=2BD,
∴2BD+BD=BC,
∴,
∵,
∴.
(3)连接BD,取BD的中点Q,连接AQ,CQ,如下图:
∵Q为BD的中点,
∴AQ是 △ ABD的中线,CQ是 △ CDB的中线,
∴,,
∴,
∴折线AQ-QC将四边形ABCD分成面积相等的两部分.
【分析】(1)由D是BC边上的中点,得AD是 △ABC的中线,,即可得到答案;
(2)作AE⊥BC于E,由CD+BD=BC,CD=2BD,得2BD+BD=BC,则,则可求出和,便可得到答案;
(3)连接BD,取BD的中点Q,连接AQ,CQ,则AQ是 △ ABD的中线,CQ是 △ CDB的中线,,,则,则可得到结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
