11.2.2 三角形的外角一课一练(含解析)
文档属性
| 名称 | 11.2.2 三角形的外角一课一练(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 904.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 08:02:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
11.2.2 三角形的外角一课一练
一、填空题
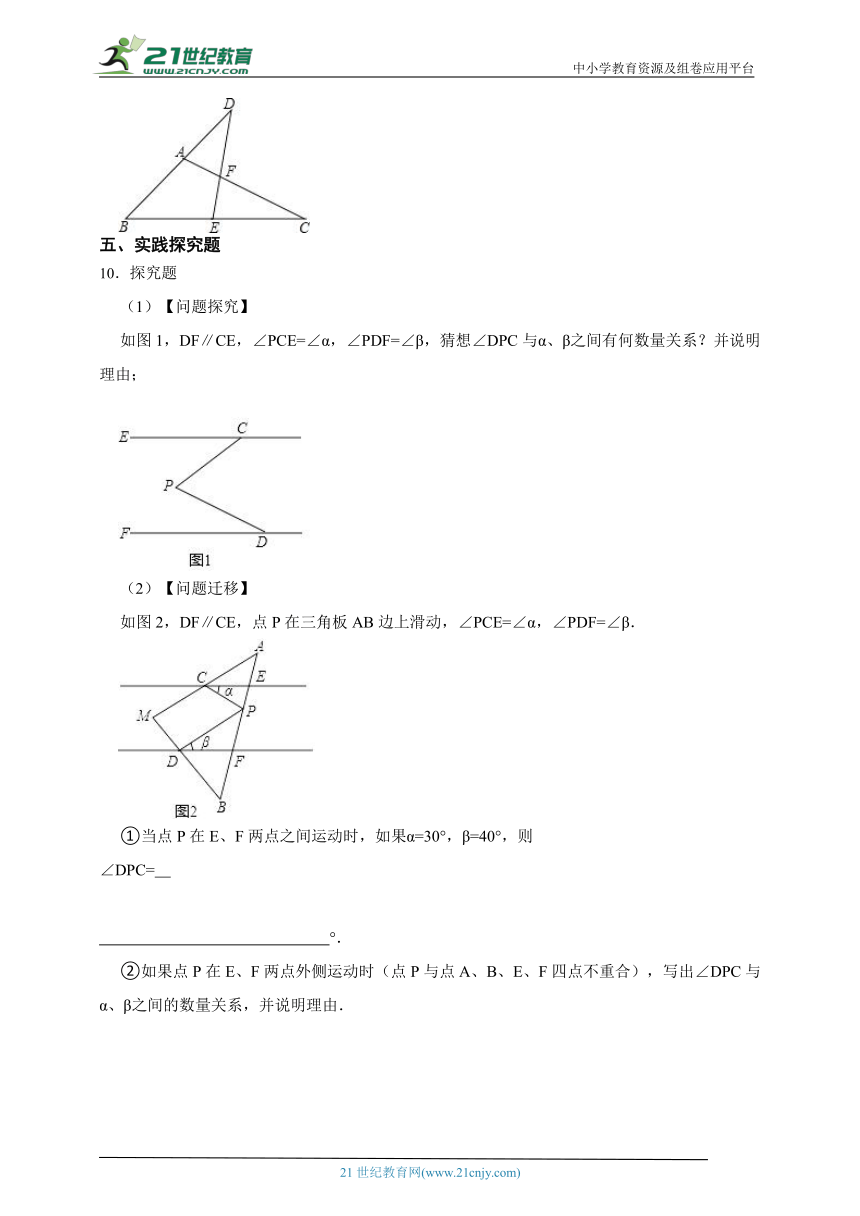
1.一副三角板如图所示放置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中的度数为 °.
2.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是 .
二、单选题
3.一把直尺和一块三角板ABC(其中∠B=30°,∠C=90°)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=50°,那么∠BAF的大小为( )
A.20° B.40° C.45° D.50°
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
6.如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( )
A.25° B.45° C.20° D.15°
7.下列图形中一定能说明∠1>∠2的是( )
A. B.
C. D.
三、解答题
8.如图,在直角△ABC中,∠ACB=90°,CD是AB边上的高,CE是△ABC的角平分线.已知∠CEB=110°,求∠ECB,∠ECD的度数.
四、计算题
9.如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
五、实践探究题
10.探究题
(1)【问题探究】
如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(2)【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
①当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
②如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
答案解析部分
1.【答案】75
【解析】【解答】解:如图所示:
∵EF∥BC,
∴∠FDC=∠F=30°,
∴∠α=∠FDC+∠C=30°+45°=75°,
故答案为:75.
【分析】由平行线的性质“两直线平行内错角相等”可得∠FDC=∠F,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”得∠α=∠FDC+∠C可求解.
2.【答案】165°
【解析】【解答】解:如下图所示
由题意可得,∠1=45°
根据三角形外角的性质可得∠2=∠1-30°=15°
∴∠α=180°-∠2=165°
故答案为:165°.
【分析】如解图所示,根据题意可得∠1=45°,然后根据三角形外角的性质即可求出∠2,最后根据平角的定义即可求出结论.
3.【答案】A
【解析】【解答】解:∵DE∥AF,
∴∠AFC=∠CDE=50°,
根据三角形外角的性质可得:∠AFC=∠B+∠BAF,
∴∠BAF=50°-30°=20°,
故答案为:A.
【分析】利用平行线的性质,可得出∠AFC=∠CDE=50°,再根据三角形的外角性质得出∠AFC=∠B+∠BAF,从而就可求出∠BAF的度数。
4.【答案】A
【解析】【解答】解:由题意可知,,
,
,
,
故答案为:A.
【分析】根据二直线平行,内错角相等求出∠DAF的度数,然后根据三角形的外角等于与之不相邻的两个内角的和求∠BDA即可.
5.【答案】C
【解析】【解答】解:如图
∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°.
故答案为:C.
【分析】对图形进行角标注,由平行线的性质可得∠1=∠B=68°,由外角的性质可得∠E+∠D=∠1,据此计算.
6.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠1=∠C,
∵∠C=45°,
∴∠1=45°,
∵∠1=∠P+∠A,
∴∠P=∠1-∠A
又∠A=25°,
∴∠P=∠1﹣∠A=45゜-25゜=20°.
故答案为:C.
【分析】根据平行线性质得出∠1=∠C=45°,根据三角形外角性质求出∠P即可.
7.【答案】C
【解析】【解答】解:A、∠1=∠2,故错误;
B、∠1和∠2的关系不能确定,故错误;
C、∠1>∠2,故正确;
D、∠1和∠2的关系不能确定,故错误;
故选:C.
【分析】根据三角形的外角的性质、对顶角的性质进行判断即可.
8.【答案】解:∵CE是△ABC的角平分线,∠ACB=90°,
∴∠ECB=45°.
∵CD是AB边上的高,∠CEB=110°,
∴∠CDB=90°,
∠ECD=110°﹣90°=20°
【解析】【分析】直接根据角平分线的定义求∠ECB=45°,利用“三角形的外角等于与它不相邻的两个内角和”求∠ECD=110°﹣90°=20°.
9.【答案】解:∵△CEF中,∠C=30°,∠EFC=70°,
∴∠FEC=80°,
∵∠FEC是△BDE的外角,且∠B=45°,
∴∠D=∠FEC﹣∠B=80°﹣45°=35°
【解析】【分析】先根据三角形内角和定理,求得∠FEC的度数,再根据三角形外角性质,求得∠D的度数.
10.【答案】(1)∠DPC=α+β.
理由:如图,延长CP交DF于A,
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
(2)① 70②如图,∠DPC=β﹣α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1﹣∠FDP=∠1﹣α.∴∠DPC=β﹣α;如图,∠DPC=α﹣β∵DF∥CE,∴∠PDF=∠1=α,∵∠DPC=∠1﹣∠ACE=∠1﹣β.∴∠DPC=α﹣β.
【解析】【分析】(1)【问题探究】延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;(2)【问题迁移】①延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;②分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
【问题迁移】(2)如图2,延长CP交DF于G,
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
11.2.2 三角形的外角一课一练
一、填空题
1.一副三角板如图所示放置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中的度数为 °.
2.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是 .
二、单选题
3.一把直尺和一块三角板ABC(其中∠B=30°,∠C=90°)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=50°,那么∠BAF的大小为( )
A.20° B.40° C.45° D.50°
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
6.如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( )
A.25° B.45° C.20° D.15°
7.下列图形中一定能说明∠1>∠2的是( )
A. B.
C. D.
三、解答题
8.如图,在直角△ABC中,∠ACB=90°,CD是AB边上的高,CE是△ABC的角平分线.已知∠CEB=110°,求∠ECB,∠ECD的度数.
四、计算题
9.如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
五、实践探究题
10.探究题
(1)【问题探究】
如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(2)【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
①当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
②如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
答案解析部分
1.【答案】75
【解析】【解答】解:如图所示:
∵EF∥BC,
∴∠FDC=∠F=30°,
∴∠α=∠FDC+∠C=30°+45°=75°,
故答案为:75.
【分析】由平行线的性质“两直线平行内错角相等”可得∠FDC=∠F,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”得∠α=∠FDC+∠C可求解.
2.【答案】165°
【解析】【解答】解:如下图所示
由题意可得,∠1=45°
根据三角形外角的性质可得∠2=∠1-30°=15°
∴∠α=180°-∠2=165°
故答案为:165°.
【分析】如解图所示,根据题意可得∠1=45°,然后根据三角形外角的性质即可求出∠2,最后根据平角的定义即可求出结论.
3.【答案】A
【解析】【解答】解:∵DE∥AF,
∴∠AFC=∠CDE=50°,
根据三角形外角的性质可得:∠AFC=∠B+∠BAF,
∴∠BAF=50°-30°=20°,
故答案为:A.
【分析】利用平行线的性质,可得出∠AFC=∠CDE=50°,再根据三角形的外角性质得出∠AFC=∠B+∠BAF,从而就可求出∠BAF的度数。
4.【答案】A
【解析】【解答】解:由题意可知,,
,
,
,
故答案为:A.
【分析】根据二直线平行,内错角相等求出∠DAF的度数,然后根据三角形的外角等于与之不相邻的两个内角的和求∠BDA即可.
5.【答案】C
【解析】【解答】解:如图
∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°.
故答案为:C.
【分析】对图形进行角标注,由平行线的性质可得∠1=∠B=68°,由外角的性质可得∠E+∠D=∠1,据此计算.
6.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠1=∠C,
∵∠C=45°,
∴∠1=45°,
∵∠1=∠P+∠A,
∴∠P=∠1-∠A
又∠A=25°,
∴∠P=∠1﹣∠A=45゜-25゜=20°.
故答案为:C.
【分析】根据平行线性质得出∠1=∠C=45°,根据三角形外角性质求出∠P即可.
7.【答案】C
【解析】【解答】解:A、∠1=∠2,故错误;
B、∠1和∠2的关系不能确定,故错误;
C、∠1>∠2,故正确;
D、∠1和∠2的关系不能确定,故错误;
故选:C.
【分析】根据三角形的外角的性质、对顶角的性质进行判断即可.
8.【答案】解:∵CE是△ABC的角平分线,∠ACB=90°,
∴∠ECB=45°.
∵CD是AB边上的高,∠CEB=110°,
∴∠CDB=90°,
∠ECD=110°﹣90°=20°
【解析】【分析】直接根据角平分线的定义求∠ECB=45°,利用“三角形的外角等于与它不相邻的两个内角和”求∠ECD=110°﹣90°=20°.
9.【答案】解:∵△CEF中,∠C=30°,∠EFC=70°,
∴∠FEC=80°,
∵∠FEC是△BDE的外角,且∠B=45°,
∴∠D=∠FEC﹣∠B=80°﹣45°=35°
【解析】【分析】先根据三角形内角和定理,求得∠FEC的度数,再根据三角形外角性质,求得∠D的度数.
10.【答案】(1)∠DPC=α+β.
理由:如图,延长CP交DF于A,
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
(2)① 70②如图,∠DPC=β﹣α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1﹣∠FDP=∠1﹣α.∴∠DPC=β﹣α;如图,∠DPC=α﹣β∵DF∥CE,∴∠PDF=∠1=α,∵∠DPC=∠1﹣∠ACE=∠1﹣β.∴∠DPC=α﹣β.
【解析】【分析】(1)【问题探究】延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;(2)【问题迁移】①延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;②分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
【问题迁移】(2)如图2,延长CP交DF于G,
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
11.2.2 三角形的外角一课一练
一、填空题
1.一副三角板如图所示放置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中的度数为 °.
2.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是 .
二、单选题
3.一把直尺和一块三角板ABC(其中∠B=30°,∠C=90°)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=50°,那么∠BAF的大小为( )
A.20° B.40° C.45° D.50°
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
6.如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( )
A.25° B.45° C.20° D.15°
7.下列图形中一定能说明∠1>∠2的是( )
A. B.
C. D.
三、解答题
8.如图,在直角△ABC中,∠ACB=90°,CD是AB边上的高,CE是△ABC的角平分线.已知∠CEB=110°,求∠ECB,∠ECD的度数.
四、计算题
9.如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
五、实践探究题
10.探究题
(1)【问题探究】
如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(2)【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
①当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
②如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
答案解析部分
1.【答案】75
【解析】【解答】解:如图所示:
∵EF∥BC,
∴∠FDC=∠F=30°,
∴∠α=∠FDC+∠C=30°+45°=75°,
故答案为:75.
【分析】由平行线的性质“两直线平行内错角相等”可得∠FDC=∠F,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”得∠α=∠FDC+∠C可求解.
2.【答案】165°
【解析】【解答】解:如下图所示
由题意可得,∠1=45°
根据三角形外角的性质可得∠2=∠1-30°=15°
∴∠α=180°-∠2=165°
故答案为:165°.
【分析】如解图所示,根据题意可得∠1=45°,然后根据三角形外角的性质即可求出∠2,最后根据平角的定义即可求出结论.
3.【答案】A
【解析】【解答】解:∵DE∥AF,
∴∠AFC=∠CDE=50°,
根据三角形外角的性质可得:∠AFC=∠B+∠BAF,
∴∠BAF=50°-30°=20°,
故答案为:A.
【分析】利用平行线的性质,可得出∠AFC=∠CDE=50°,再根据三角形的外角性质得出∠AFC=∠B+∠BAF,从而就可求出∠BAF的度数。
4.【答案】A
【解析】【解答】解:由题意可知,,
,
,
,
故答案为:A.
【分析】根据二直线平行,内错角相等求出∠DAF的度数,然后根据三角形的外角等于与之不相邻的两个内角的和求∠BDA即可.
5.【答案】C
【解析】【解答】解:如图
∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°.
故答案为:C.
【分析】对图形进行角标注,由平行线的性质可得∠1=∠B=68°,由外角的性质可得∠E+∠D=∠1,据此计算.
6.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠1=∠C,
∵∠C=45°,
∴∠1=45°,
∵∠1=∠P+∠A,
∴∠P=∠1-∠A
又∠A=25°,
∴∠P=∠1﹣∠A=45゜-25゜=20°.
故答案为:C.
【分析】根据平行线性质得出∠1=∠C=45°,根据三角形外角性质求出∠P即可.
7.【答案】C
【解析】【解答】解:A、∠1=∠2,故错误;
B、∠1和∠2的关系不能确定,故错误;
C、∠1>∠2,故正确;
D、∠1和∠2的关系不能确定,故错误;
故选:C.
【分析】根据三角形的外角的性质、对顶角的性质进行判断即可.
8.【答案】解:∵CE是△ABC的角平分线,∠ACB=90°,
∴∠ECB=45°.
∵CD是AB边上的高,∠CEB=110°,
∴∠CDB=90°,
∠ECD=110°﹣90°=20°
【解析】【分析】直接根据角平分线的定义求∠ECB=45°,利用“三角形的外角等于与它不相邻的两个内角和”求∠ECD=110°﹣90°=20°.
9.【答案】解:∵△CEF中,∠C=30°,∠EFC=70°,
∴∠FEC=80°,
∵∠FEC是△BDE的外角,且∠B=45°,
∴∠D=∠FEC﹣∠B=80°﹣45°=35°
【解析】【分析】先根据三角形内角和定理,求得∠FEC的度数,再根据三角形外角性质,求得∠D的度数.
10.【答案】(1)∠DPC=α+β.
理由:如图,延长CP交DF于A,
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
(2)① 70②如图,∠DPC=β﹣α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1﹣∠FDP=∠1﹣α.∴∠DPC=β﹣α;如图,∠DPC=α﹣β∵DF∥CE,∴∠PDF=∠1=α,∵∠DPC=∠1﹣∠ACE=∠1﹣β.∴∠DPC=α﹣β.
【解析】【分析】(1)【问题探究】延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;(2)【问题迁移】①延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;②分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
【问题迁移】(2)如图2,延长CP交DF于G,
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
11.2.2 三角形的外角一课一练
一、填空题
1.一副三角板如图所示放置,两三角板的斜边互相平行,每个三角板的直角顶点都在另一个三角板的斜边上,图中的度数为 °.
2.一副三角板有一个含30°角的直角三角形和一个含45°角的直角三角形,如图叠放在一起,则∠α的度数是 .
二、单选题
3.一把直尺和一块三角板ABC(其中∠B=30°,∠C=90°)摆放位置如图所示,直尺一边与三角板的两直角边分别交于点D,点E,另一边与三角板的两直角边分别交于点F,点A,且∠CDE=50°,那么∠BAF的大小为( )
A.20° B.40° C.45° D.50°
4.小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.如图,AB∥CD,∠B=68°,∠E=20°,则∠D的度数为( )
A.28° B.38° C.48° D.88°
6.如图,直线AB∥CD,∠A=25°,∠C=45°,则∠P的度数为( )
A.25° B.45° C.20° D.15°
7.下列图形中一定能说明∠1>∠2的是( )
A. B.
C. D.
三、解答题
8.如图,在直角△ABC中,∠ACB=90°,CD是AB边上的高,CE是△ABC的角平分线.已知∠CEB=110°,求∠ECB,∠ECD的度数.
四、计算题
9.如图,E为△ABC的边BC上一点,D在BA的延长线上,DE交AC于点F,∠B=45°,∠C=30°,∠EFC=70°,求∠D的度数.
五、实践探究题
10.探究题
(1)【问题探究】
如图1,DF∥CE,∠PCE=∠α,∠PDF=∠β,猜想∠DPC与α、β之间有何数量关系?并说明理由;
(2)【问题迁移】
如图2,DF∥CE,点P在三角板AB边上滑动,∠PCE=∠α,∠PDF=∠β.
①当点P在E、F两点之间运动时,如果α=30°,β=40°,则∠DPC= °.
②如果点P在E、F两点外侧运动时(点P与点A、B、E、F四点不重合),写出∠DPC与α、β之间的数量关系,并说明理由.
答案解析部分
1.【答案】75
【解析】【解答】解:如图所示:
∵EF∥BC,
∴∠FDC=∠F=30°,
∴∠α=∠FDC+∠C=30°+45°=75°,
故答案为:75.
【分析】由平行线的性质“两直线平行内错角相等”可得∠FDC=∠F,然后根据三角形的外角的性质“三角形的一个外角等于和它不相邻的两个内角的和”得∠α=∠FDC+∠C可求解.
2.【答案】165°
【解析】【解答】解:如下图所示
由题意可得,∠1=45°
根据三角形外角的性质可得∠2=∠1-30°=15°
∴∠α=180°-∠2=165°
故答案为:165°.
【分析】如解图所示,根据题意可得∠1=45°,然后根据三角形外角的性质即可求出∠2,最后根据平角的定义即可求出结论.
3.【答案】A
【解析】【解答】解:∵DE∥AF,
∴∠AFC=∠CDE=50°,
根据三角形外角的性质可得:∠AFC=∠B+∠BAF,
∴∠BAF=50°-30°=20°,
故答案为:A.
【分析】利用平行线的性质,可得出∠AFC=∠CDE=50°,再根据三角形的外角性质得出∠AFC=∠B+∠BAF,从而就可求出∠BAF的度数。
4.【答案】A
【解析】【解答】解:由题意可知,,
,
,
,
故答案为:A.
【分析】根据二直线平行,内错角相等求出∠DAF的度数,然后根据三角形的外角等于与之不相邻的两个内角的和求∠BDA即可.
5.【答案】C
【解析】【解答】解:如图
∵AB∥CD,
∴∠1=∠B=68°,
∵∠E=20°,
∴∠D=∠1﹣∠E=48°.
故答案为:C.
【分析】对图形进行角标注,由平行线的性质可得∠1=∠B=68°,由外角的性质可得∠E+∠D=∠1,据此计算.
6.【答案】C
【解析】【解答】解:如图,
∵AB∥CD,
∴∠1=∠C,
∵∠C=45°,
∴∠1=45°,
∵∠1=∠P+∠A,
∴∠P=∠1-∠A
又∠A=25°,
∴∠P=∠1﹣∠A=45゜-25゜=20°.
故答案为:C.
【分析】根据平行线性质得出∠1=∠C=45°,根据三角形外角性质求出∠P即可.
7.【答案】C
【解析】【解答】解:A、∠1=∠2,故错误;
B、∠1和∠2的关系不能确定,故错误;
C、∠1>∠2,故正确;
D、∠1和∠2的关系不能确定,故错误;
故选:C.
【分析】根据三角形的外角的性质、对顶角的性质进行判断即可.
8.【答案】解:∵CE是△ABC的角平分线,∠ACB=90°,
∴∠ECB=45°.
∵CD是AB边上的高,∠CEB=110°,
∴∠CDB=90°,
∠ECD=110°﹣90°=20°
【解析】【分析】直接根据角平分线的定义求∠ECB=45°,利用“三角形的外角等于与它不相邻的两个内角和”求∠ECD=110°﹣90°=20°.
9.【答案】解:∵△CEF中,∠C=30°,∠EFC=70°,
∴∠FEC=80°,
∵∠FEC是△BDE的外角,且∠B=45°,
∴∠D=∠FEC﹣∠B=80°﹣45°=35°
【解析】【分析】先根据三角形内角和定理,求得∠FEC的度数,再根据三角形外角性质,求得∠D的度数.
10.【答案】(1)∠DPC=α+β.
理由:如图,延长CP交DF于A,
∵DF∥CE,
∴∠PCE=∠1=α,
∵∠DPC=∠2+∠1=180°﹣∠APD,
∴∠DPC=∠2+∠PCE=α+β;
(2)① 70②如图,∠DPC=β﹣α∵DF∥CE,∴∠PCE=∠1=β,∵∠DPC=∠1﹣∠FDP=∠1﹣α.∴∠DPC=β﹣α;如图,∠DPC=α﹣β∵DF∥CE,∴∠PDF=∠1=α,∵∠DPC=∠1﹣∠ACE=∠1﹣β.∴∠DPC=α﹣β.
【解析】【分析】(1)【问题探究】延长CP交DF于A,根据平行线的性质以及三角形外角性质进行计算即可;(2)【问题迁移】①延长CP交DF于G,根据平行线的性质以及三角形外角性质进行计算即可;②分两种情况进行讨论:点P在BF上,点P在AE上,分别根据平行线的性质以及三角形外角性质进行计算即可.
【问题迁移】(2)如图2,延长CP交DF于G,
∵DF∥CE,
∴∠PCE=∠G=30°,
∴∠DPC=∠G+∠GDP=30°+40°=70°,
故答案为:70;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
