3.1 字母表示数 课件(30张PPT)
文档属性
| 名称 | 3.1 字母表示数 课件(30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
北师大版 数学 七年级上册
1 字母表示数
第三章 整式及其加减
学习目标
1.理解用字母表示数的意义.(重点)
2.能用字母表示以前学过的运算律和计算公式.
3.能用字母表示一些简单问题中的数量关系和变化规律.(难点)
一、导入新课
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水……
n只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水.
15
30
60
15
n
2n
4n
n
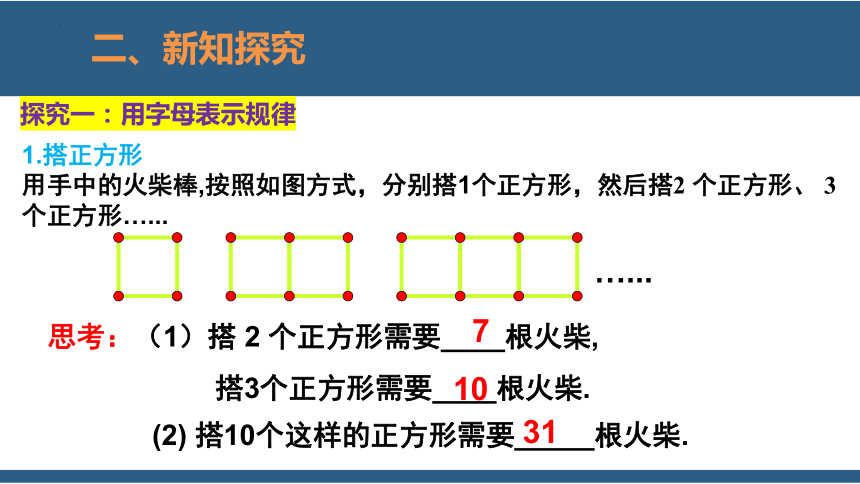
思考:(1)搭 2 个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭10个这样的正方形需要_____根火柴.
二、新知探究
1.搭正方形
用手中的火柴棒,按照如图方式,分别搭1个正方形,然后搭2 个正方形、 3 个正方形…...
…...
7
10
31
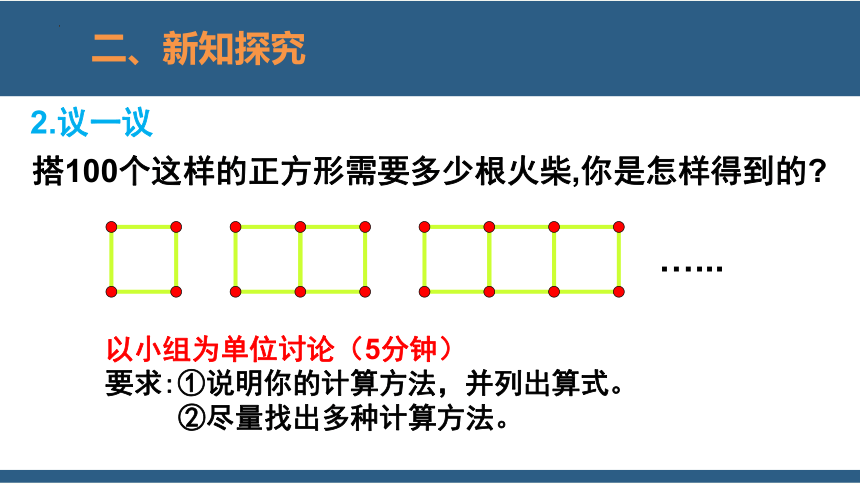
二、新知探究
搭100个这样的正方形需要多少根火柴,你是怎样得到的
2.议一议
…...
以小组为单位讨论(5分钟)
要求:①说明你的计算方法,并列出算式。
②尽量找出多种计算方法。
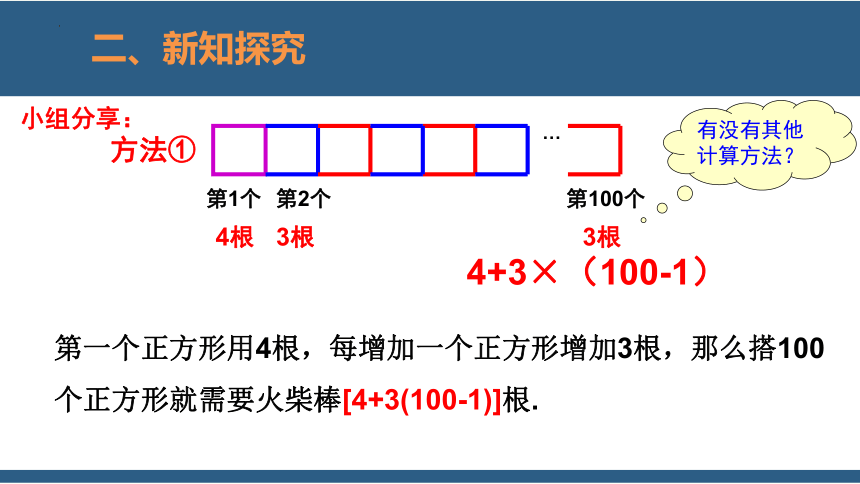
二、新知探究
…
第1个
4根
第2个
第100个
3根
3根
小组分享:
方法①
4+3×(100-1)
有没有其他计算方法?
第一个正方形用4根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒[4+3(100-1)]根.
二、新知探究
…
先摆 1根
第1个
3根
第100个
3根
方法②
1+3×100
第一个正方形用(1+3)根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒(1+3×100)根.
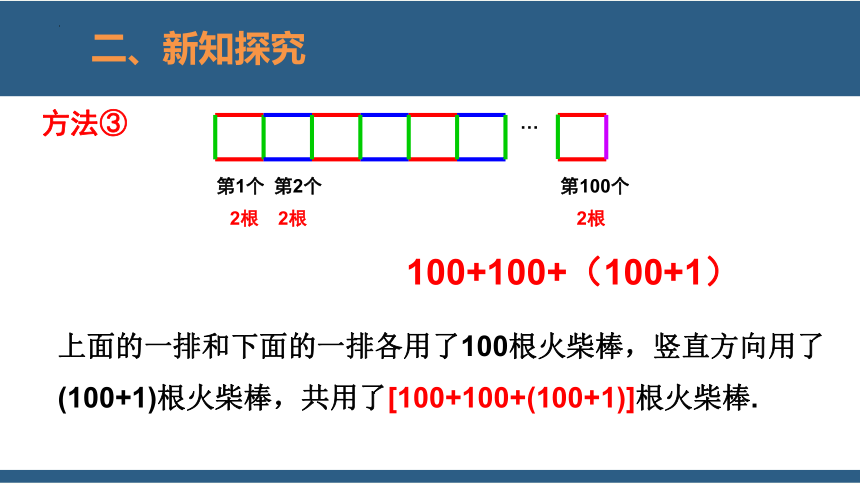
二、新知探究
…
第1个
2根
第2个
2根
第100个
2根
方法③
100+100+(100+1)
上面的一排和下面的一排各用了100根火柴棒,竖直方向用了 (100+1)根火柴棒,共用了[100+100+(100+1)]根火柴棒.
二、新知探究
…
第1个
4根
第100个
4根
…
方法④
4×100-(100-1)
先分开摆放100个正方形用4×100根,再拼在一起,去掉重复的(100-1)根,那么搭100个正方形就需要火柴棒4×100-(100-1)根.
二、新知探究
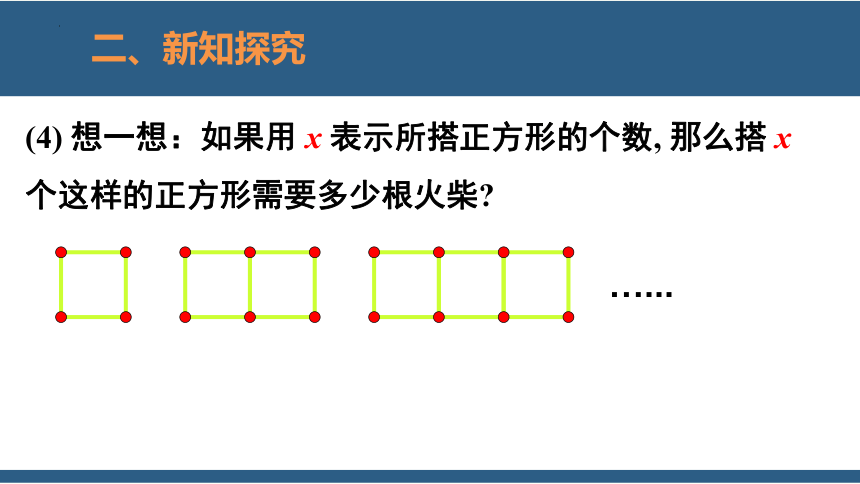
(4) 想一想:如果用 x 表示所搭正方形的个数, 那么搭 x 个这样的正方形需要多少根火柴
…...
二、新知探究
…
第1个
4根
第2个
第x个
3根
3根
方法①
二、新知探究
…
先摆 1根
第1个
3根
第x个
3根
方法②
二、新知探究
…
第1个
2根
第2个
2根
第x个
2根
方法③
二、新知探究
…
第1个
4根
第x个
4根
方法④
(2)搭1000个这样的正方形需要_______根火柴棒; 搭1500个这样的正方形需要_______根火柴棒.
二、新知探究
3.问题解决
(1)根据以上计算方法,搭200个这样的正方形需要______根火柴棒;
例如:利用方法①的式子,用200代替4+3(x-1)中的x,可以得到
4+3×(200-1)=601.
601
3001
4501
规律的探索往往要经历从特殊(具体实例)到一般(用字母表示)再到特殊(验证)的过程.
1.用字母表示周长、面积、体积等公式:
(1)三角形的面积: (a表示底边长,h表示对应的高).
(2)长方形的周长: ;面积: (m,n分别表示长方形的长和宽).
(3)圆的周长: ,面积: (r表示圆的半径).
(4)长方体的体积: (a,b,c分别表示长方体的长、宽、高).
二、新知探究
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系.你在以前的学习中有哪些地方用到了字母?这些字母都表示什么?
V=abc
C=2m+2n
S=mn
C=2πr
S=πr2
3.用字母表示我们学过的公式和法则:
(1)用a,b表示有理数,那么有理数的减法法则可以表示成:
;
(2)用a,b表示有理数,b不等于0,那么有理数的除法法则可以表示成:
.
(1)加法交换律: ;(2)加法结合律: ;
(3)乘法交换律: ;(4)乘法结合律: ;
(5)分配律: .
2.用字母表示有理数的运算律
二、新知探究
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
a-b=a+(-b)
二、新知探究
字母可以表示任何数。
知识归纳
注意:同一个字母,在不同的问题中可以代表不同的量;
在同一问题中,不同的量要用不同的字母来表示.
用字母表示数,能把数量和数量关系一般而又简明地表达出来,从而为描述和研究问题带来方便.
二、新知探究
1.小明步行上学,速度为v 米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
3v
数字和字母相乘时,省略乘号,并把数字写在字母的前面.
2.某练习簿的单价为a元,b本练习簿的总价是 元.
字母和字母相乘时,乘号可以用“·”代替或省略不写。
ab
二、新知探究
4.购买单价为a元/个的物品10个,若支付b元(b>10a),则应找回
元;
除法运算写成分数形式。
3.小明用t秒走了s米,它的速度为_______米/秒.
(b-10a)
若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面;若式子是积或商的形式,则将单位名称写在式子的后面即可.
例1:如图所示,如果用20米长的铝合金做一个长方形的窗框,设长方形窗框的三根横条长均为a米,则长方形窗框的竖条长均为________米.
三、典例精析
a
a
a
例2:如图所示,用若干张大小相同的灰、白两种颜色的正方形纸片拼图,第1个图需要4张灰色正方形纸片.
(1)第2个图需要____张灰色正方形纸片,第3个图需要____张灰色正方形纸片;
(2)第10个图需要 张灰色正方形纸片;
(3)第n个图需要多少张灰色正方形纸片?你是怎样得到的?
三、典例精析
7
10
31
(3)方法一:如图,把每个图形分上、中、下三行,第1个图中灰色正方形纸片的张数为1+2+1,第2个图中灰色正方形纸片的张数为2+3+2,第3个图中灰色正方形纸片的张数为3+4+3……依次类推,可得第n个图中灰色正方形纸片的张数为n+(n+1)+n.
三、典例精析
方法二:如图,把每个图按灰色正方形纸片张数三、一拆分,第1个图中灰色正方形纸片的张数为3+1,第2个图中灰色正方形纸片的张数为3+3+1,第3个图中灰色正方形纸片的张数为3+3+3+1……依次类推,第n个图中灰色正方形纸片的张数为3n+1.
四、当堂练习
B
A
5.如图, 用字母表示图中
阴影部分的面积是_________.
m
n
p
q
四、当堂练习
3.某市某日的温差为11 ℃,最高气温为t ℃,则最低气温可表示为 ℃.
4.假设k是一个奇数,则比k大且与k相邻的一个奇数是 .
mn-pq
(t-11)
k+2
6.用一根长为a cm的铁丝,首尾相接围成一个正方形,要将它按图中所示的方式向外等距扩1cm得到一个新的正方形,则新正方形的边长是________ cm.
四、当堂练习
7.超市卖了x瓶啤酒和y瓶矿泉水,已知啤酒每瓶5元,矿泉水每瓶1.5元,则超市共卖了 元。
8.某厂去年的产值是p万元,今年的产值比去年的2倍少3万元,今年的产值是 万元。
(2p-3)
(5x+1.5y)
四、当堂练习
图形编号 1 2 3 4 …… n
火柴棒根数
7
12
17
……
5n+2
22
9.用火柴棒按下面方式搭图,填写表格
…
①
②
③
四、当堂练习
10.用棋子摆成下列一组图案:
…
①
②
③
(1) 填写下表:
图案编号 ① ② ③ ④ ⑤ ⑩
棋子个数
(2)摆第 n 个图案需要____个棋子.
3
6
9
12
15
30
300
3n
五、课堂小结
用字母表示数量和数量关系
用字母表示规律
字母表示数
特殊(具体实例)→一般(用字母表示)
→特殊(验证)
1.字母可以表示任何数;
2.用字母表示周长、面积、体积等公式;
3.用字母表示数的运算律和公式法则;
六、作业布置
习题3.1
北师大版 数学 七年级上册
1 字母表示数
第三章 整式及其加减
学习目标
1.理解用字母表示数的意义.(重点)
2.能用字母表示以前学过的运算律和计算公式.
3.能用字母表示一些简单问题中的数量关系和变化规律.(难点)
一、导入新课
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水……
n只青蛙, 张嘴, 只眼睛, 条腿, 声扑通跳下水.
15
30
60
15
n
2n
4n
n
思考:(1)搭 2 个正方形需要____根火柴,
搭3个正方形需要____根火柴.
(2) 搭10个这样的正方形需要_____根火柴.
二、新知探究
1.搭正方形
用手中的火柴棒,按照如图方式,分别搭1个正方形,然后搭2 个正方形、 3 个正方形…...
…...
7
10
31
二、新知探究
搭100个这样的正方形需要多少根火柴,你是怎样得到的
2.议一议
…...
以小组为单位讨论(5分钟)
要求:①说明你的计算方法,并列出算式。
②尽量找出多种计算方法。
二、新知探究
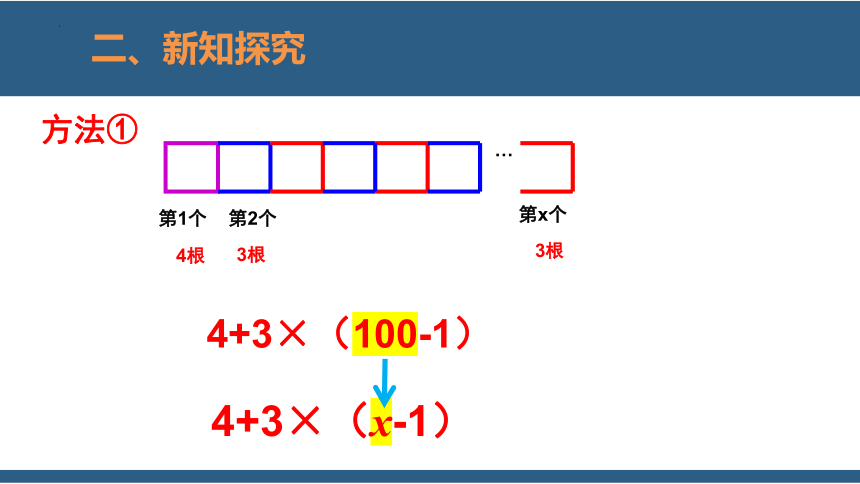
…
第1个
4根
第2个
第100个
3根
3根
小组分享:
方法①
4+3×(100-1)
有没有其他计算方法?
第一个正方形用4根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒[4+3(100-1)]根.
二、新知探究
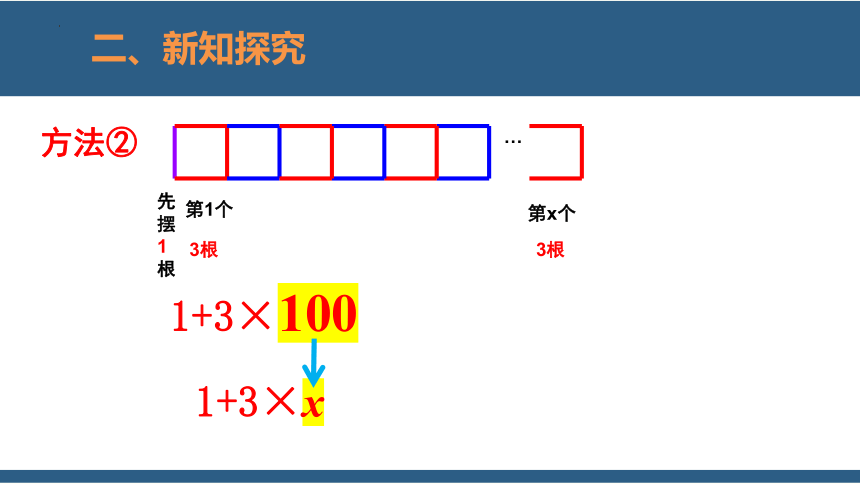
…
先摆 1根
第1个
3根
第100个
3根
方法②
1+3×100
第一个正方形用(1+3)根,每增加一个正方形增加3根,那么搭100个正方形就需要火柴棒(1+3×100)根.
二、新知探究
…
第1个
2根
第2个
2根
第100个
2根
方法③
100+100+(100+1)
上面的一排和下面的一排各用了100根火柴棒,竖直方向用了 (100+1)根火柴棒,共用了[100+100+(100+1)]根火柴棒.
二、新知探究
…
第1个
4根
第100个
4根
…
方法④
4×100-(100-1)
先分开摆放100个正方形用4×100根,再拼在一起,去掉重复的(100-1)根,那么搭100个正方形就需要火柴棒4×100-(100-1)根.
二、新知探究
(4) 想一想:如果用 x 表示所搭正方形的个数, 那么搭 x 个这样的正方形需要多少根火柴
…...
二、新知探究
…
第1个
4根
第2个
第x个
3根
3根
方法①
二、新知探究
…
先摆 1根
第1个
3根
第x个
3根
方法②
二、新知探究
…
第1个
2根
第2个
2根
第x个
2根
方法③
二、新知探究
…
第1个
4根
第x个
4根
方法④
(2)搭1000个这样的正方形需要_______根火柴棒; 搭1500个这样的正方形需要_______根火柴棒.
二、新知探究
3.问题解决
(1)根据以上计算方法,搭200个这样的正方形需要______根火柴棒;
例如:利用方法①的式子,用200代替4+3(x-1)中的x,可以得到
4+3×(200-1)=601.
601
3001
4501
规律的探索往往要经历从特殊(具体实例)到一般(用字母表示)再到特殊(验证)的过程.
1.用字母表示周长、面积、体积等公式:
(1)三角形的面积: (a表示底边长,h表示对应的高).
(2)长方形的周长: ;面积: (m,n分别表示长方形的长和宽).
(3)圆的周长: ,面积: (r表示圆的半径).
(4)长方体的体积: (a,b,c分别表示长方体的长、宽、高).
二、新知探究
在上面的活动中,我们借助字母描述了正方形的个数和火柴棒的根数之间的关系.你在以前的学习中有哪些地方用到了字母?这些字母都表示什么?
V=abc
C=2m+2n
S=mn
C=2πr
S=πr2
3.用字母表示我们学过的公式和法则:
(1)用a,b表示有理数,那么有理数的减法法则可以表示成:
;
(2)用a,b表示有理数,b不等于0,那么有理数的除法法则可以表示成:
.
(1)加法交换律: ;(2)加法结合律: ;
(3)乘法交换律: ;(4)乘法结合律: ;
(5)分配律: .
2.用字母表示有理数的运算律
二、新知探究
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
a-b=a+(-b)
二、新知探究
字母可以表示任何数。
知识归纳
注意:同一个字母,在不同的问题中可以代表不同的量;
在同一问题中,不同的量要用不同的字母来表示.
用字母表示数,能把数量和数量关系一般而又简明地表达出来,从而为描述和研究问题带来方便.
二、新知探究
1.小明步行上学,速度为v 米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为_______米/秒.
3v
数字和字母相乘时,省略乘号,并把数字写在字母的前面.
2.某练习簿的单价为a元,b本练习簿的总价是 元.
字母和字母相乘时,乘号可以用“·”代替或省略不写。
ab
二、新知探究
4.购买单价为a元/个的物品10个,若支付b元(b>10a),则应找回
元;
除法运算写成分数形式。
3.小明用t秒走了s米,它的速度为_______米/秒.
(b-10a)
若式子是和或差的形式,则应把整个式子用括号括起来,再将单位名称写在后面;若式子是积或商的形式,则将单位名称写在式子的后面即可.
例1:如图所示,如果用20米长的铝合金做一个长方形的窗框,设长方形窗框的三根横条长均为a米,则长方形窗框的竖条长均为________米.
三、典例精析
a
a
a
例2:如图所示,用若干张大小相同的灰、白两种颜色的正方形纸片拼图,第1个图需要4张灰色正方形纸片.
(1)第2个图需要____张灰色正方形纸片,第3个图需要____张灰色正方形纸片;
(2)第10个图需要 张灰色正方形纸片;
(3)第n个图需要多少张灰色正方形纸片?你是怎样得到的?
三、典例精析
7
10
31
(3)方法一:如图,把每个图形分上、中、下三行,第1个图中灰色正方形纸片的张数为1+2+1,第2个图中灰色正方形纸片的张数为2+3+2,第3个图中灰色正方形纸片的张数为3+4+3……依次类推,可得第n个图中灰色正方形纸片的张数为n+(n+1)+n.
三、典例精析
方法二:如图,把每个图按灰色正方形纸片张数三、一拆分,第1个图中灰色正方形纸片的张数为3+1,第2个图中灰色正方形纸片的张数为3+3+1,第3个图中灰色正方形纸片的张数为3+3+3+1……依次类推,第n个图中灰色正方形纸片的张数为3n+1.
四、当堂练习
B
A
5.如图, 用字母表示图中
阴影部分的面积是_________.
m
n
p
q
四、当堂练习
3.某市某日的温差为11 ℃,最高气温为t ℃,则最低气温可表示为 ℃.
4.假设k是一个奇数,则比k大且与k相邻的一个奇数是 .
mn-pq
(t-11)
k+2
6.用一根长为a cm的铁丝,首尾相接围成一个正方形,要将它按图中所示的方式向外等距扩1cm得到一个新的正方形,则新正方形的边长是________ cm.
四、当堂练习
7.超市卖了x瓶啤酒和y瓶矿泉水,已知啤酒每瓶5元,矿泉水每瓶1.5元,则超市共卖了 元。
8.某厂去年的产值是p万元,今年的产值比去年的2倍少3万元,今年的产值是 万元。
(2p-3)
(5x+1.5y)
四、当堂练习
图形编号 1 2 3 4 …… n
火柴棒根数
7
12
17
……
5n+2
22
9.用火柴棒按下面方式搭图,填写表格
…
①
②
③
四、当堂练习
10.用棋子摆成下列一组图案:
…
①
②
③
(1) 填写下表:
图案编号 ① ② ③ ④ ⑤ ⑩
棋子个数
(2)摆第 n 个图案需要____个棋子.
3
6
9
12
15
30
300
3n
五、课堂小结
用字母表示数量和数量关系
用字母表示规律
字母表示数
特殊(具体实例)→一般(用字母表示)
→特殊(验证)
1.字母可以表示任何数;
2.用字母表示周长、面积、体积等公式;
3.用字母表示数的运算律和公式法则;
六、作业布置
习题3.1
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
