3.1 字母表示数 课件(18张PPT)
文档属性
| 名称 | 3.1 字母表示数 课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 98.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 09:33:19 | ||
图片预览





文档简介
(共18张PPT)
教学目标
01
借助生活实例,理解用字母表示数的充分性和必要性
02
能用含有字母的式子表示简单的数量、数量关系、计算公式等
看到这些图标,你想到了什么?
音乐、音符
禁止拍照
危险警告
雷阵雨
在生活中,我们经常用图标表示某种含义~
在数学中,我们经常用字母表示数~
01
情境引入
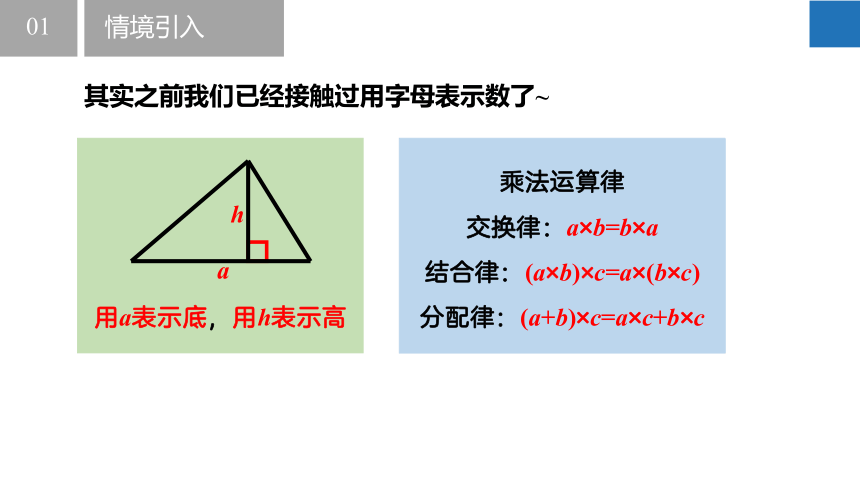
其实之前我们已经接触过用字母表示数了~
用a表示底,用h表示高
a
h
01
情境引入
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
用同样大小的两种不同颜色的正方体纸片,按下图的方式拼正方形。
第1个图形中有1个小正方形
第2个图形比第1个图形多____个小正方形
第3个图形比第2个图形多____个小正方形
3
5
02
知识精讲
…
第10个图形比第9个图形多几个小正方形?
第100个图形比第99个图形多几个小正方形?
第n个图形比第n-1个图形多几个小正方形?
02
知识精讲
第4个图形比第3个图形多____个小正方形
7
02
知识精讲
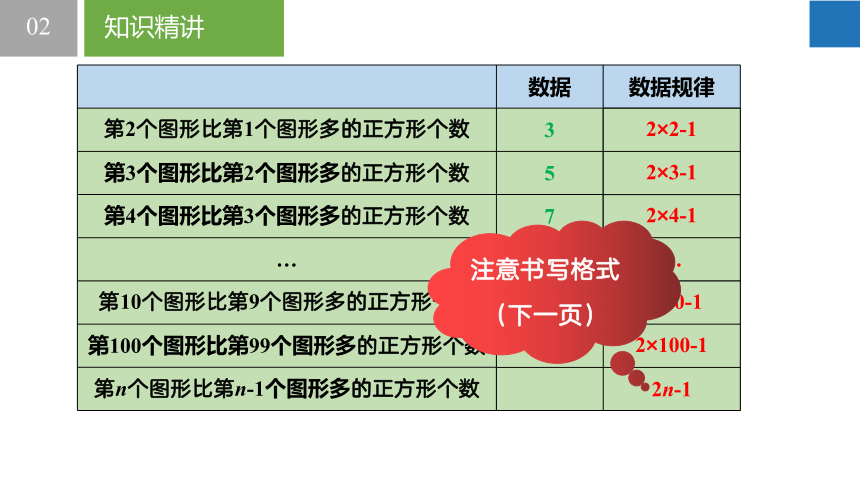
数据 数据规律
第2个图形比第1个图形多的正方形个数 3
第3个图形比第2个图形多的正方形个数 5
第4个图形比第3个图形多的正方形个数 7
… …
第10个图形比第9个图形多的正方形个数
第100个图形比第99个图形多的正方形个数
第n个图形比第n-1个图形多的正方形个数
2×2-1
2×3-1
2×4-1
…
99 2×10-1
199 2×100-1
2n-1
注意书写格式(下一页)
注意1:数与字母相乘时,若出现乘号,通常写作“·”或省略不写,且数写在字母前。
但是数与数相乘时,为了避免歧义,只能用乘号,不能用“·”或省略。
02
知识精讲
判断下列写法是否正确~
(1)100×a
(2)a100
(3)100·520
× 100·a或100a
× 100×520
02
知识精讲
例1、用字母表示数
(1)小明今年n岁,小明比小丽大2岁,小丽今年_____岁;
(2)小丽th走了skm,她的平均速度是_____km/h;
(3)一件羊毛衫标价a元,如果按标价的80%(8折)出售,那么这件羊毛衫的售价是_____元;
(n-2)
80%a
03
典例精析
注意2:含有字母的式子用“+”或“-”连接时,后面有单位,要用“( )”将这个式子括起来。
注意3:除法一般写成分数形式。
例1、用字母表示数
(4)一个长方形的长是宽的2倍,如果宽为am,那么这个长方形的面积是_____m2;
(5)一套校服,上衣a元,裤子比上衣便宜15元,裤子_____元;
(6)练习本每本m元,小丽买了5本,小亮买了2本,小丽比小亮多用_____元;
2a2
(a-15)
3m
03
典例精析
例1、用字母表示数
(7)学生剧场的楼上有a个座位,楼下有b个座位,楼上楼下共有座位_____个;
(8)公共汽车上有40人,到达某站后,下车m人,上车n人,这时车上共有_______人.
(a+b)
(40-m+n)
用字母表示数,可使问题中的数量表示更简明,更具有一般性
03
典例精析
例2-1、用字母表示数
(1)a与b的平方的和
(2)a与b的和的平方
(3)a的相反数与y的2倍的比
03
典例精析
a+b2
(a+b)2
例2-2、下列代数式用自然语言的表示中错误的是( )
A.a2-2ab+b2表示a,b两数的平方和减去它们乘积的2倍
B.m+2n表示m与n的2倍的和
C.a2+b2表示a与b的平方的和
D.(a+b)(a-b)表示a,b两数的和与差的乘积
C
03
典例精析
表示a平方与b的平方的和
例3-1、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格
B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价
D.该物品价格上涨10%时上涨的价格
03
典例精析
B
例3-2、某品牌服装专卖店一款服装按原价降价a元后,再降价20%,现售价为x元,则原售价为_____。
03
典例精析
例4、能用代数式a+0.3a表示含义的是( )
A.妈妈在超市购买物品共需a元,结账时买塑料袋又花了0.3元,妈妈共花了多少元
B.一个长方形的长是a米,宽是0.3a米,这个长方形的周长是多少米
C.小明骑自行车以a千米/小时的速度行驶0.3a小时后,所行驶的路程是多少千米
D.一套商品房原价为a万元,现提价30%,那么现在的售价是多少万元
a+0.3
D
03
典例精析
2(a+0.3a)=2.6a
0.3a2
课后总结
用字母表示数的注意事项:
下节课还会继续补充和强调哦~
注意1:数与字母相乘时,若出现乘号,通常写作“·”或省略不写,且数写在字母前。
注意2:含有字母的式子用“+”或“-”连接时,后面有单位,要用“( )”将这个式子括起来。
注意3:除法一般写成分数形式。
教学目标
01
借助生活实例,理解用字母表示数的充分性和必要性
02
能用含有字母的式子表示简单的数量、数量关系、计算公式等
看到这些图标,你想到了什么?
音乐、音符
禁止拍照
危险警告
雷阵雨
在生活中,我们经常用图标表示某种含义~
在数学中,我们经常用字母表示数~
01
情境引入
其实之前我们已经接触过用字母表示数了~
用a表示底,用h表示高
a
h
01
情境引入
乘法运算律
交换律:a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:(a+b)×c=a×c+b×c
用同样大小的两种不同颜色的正方体纸片,按下图的方式拼正方形。
第1个图形中有1个小正方形
第2个图形比第1个图形多____个小正方形
第3个图形比第2个图形多____个小正方形
3
5
02
知识精讲
…
第10个图形比第9个图形多几个小正方形?
第100个图形比第99个图形多几个小正方形?
第n个图形比第n-1个图形多几个小正方形?
02
知识精讲
第4个图形比第3个图形多____个小正方形
7
02
知识精讲
数据 数据规律
第2个图形比第1个图形多的正方形个数 3
第3个图形比第2个图形多的正方形个数 5
第4个图形比第3个图形多的正方形个数 7
… …
第10个图形比第9个图形多的正方形个数
第100个图形比第99个图形多的正方形个数
第n个图形比第n-1个图形多的正方形个数
2×2-1
2×3-1
2×4-1
…
99 2×10-1
199 2×100-1
2n-1
注意书写格式(下一页)
注意1:数与字母相乘时,若出现乘号,通常写作“·”或省略不写,且数写在字母前。
但是数与数相乘时,为了避免歧义,只能用乘号,不能用“·”或省略。
02
知识精讲
判断下列写法是否正确~
(1)100×a
(2)a100
(3)100·520
× 100·a或100a
× 100×520
02
知识精讲
例1、用字母表示数
(1)小明今年n岁,小明比小丽大2岁,小丽今年_____岁;
(2)小丽th走了skm,她的平均速度是_____km/h;
(3)一件羊毛衫标价a元,如果按标价的80%(8折)出售,那么这件羊毛衫的售价是_____元;
(n-2)
80%a
03
典例精析
注意2:含有字母的式子用“+”或“-”连接时,后面有单位,要用“( )”将这个式子括起来。
注意3:除法一般写成分数形式。
例1、用字母表示数
(4)一个长方形的长是宽的2倍,如果宽为am,那么这个长方形的面积是_____m2;
(5)一套校服,上衣a元,裤子比上衣便宜15元,裤子_____元;
(6)练习本每本m元,小丽买了5本,小亮买了2本,小丽比小亮多用_____元;
2a2
(a-15)
3m
03
典例精析
例1、用字母表示数
(7)学生剧场的楼上有a个座位,楼下有b个座位,楼上楼下共有座位_____个;
(8)公共汽车上有40人,到达某站后,下车m人,上车n人,这时车上共有_______人.
(a+b)
(40-m+n)
用字母表示数,可使问题中的数量表示更简明,更具有一般性
03
典例精析
例2-1、用字母表示数
(1)a与b的平方的和
(2)a与b的和的平方
(3)a的相反数与y的2倍的比
03
典例精析
a+b2
(a+b)2
例2-2、下列代数式用自然语言的表示中错误的是( )
A.a2-2ab+b2表示a,b两数的平方和减去它们乘积的2倍
B.m+2n表示m与n的2倍的和
C.a2+b2表示a与b的平方的和
D.(a+b)(a-b)表示a,b两数的和与差的乘积
C
03
典例精析
表示a平方与b的平方的和
例3-1、若x表示某件物品的原价,则代数式(1+10%)x表示的意义是( )
A.该物品打九折后的价格
B.该物品价格上涨10%后的售价
C.该物品价格下降10%后的售价
D.该物品价格上涨10%时上涨的价格
03
典例精析
B
例3-2、某品牌服装专卖店一款服装按原价降价a元后,再降价20%,现售价为x元,则原售价为_____。
03
典例精析
例4、能用代数式a+0.3a表示含义的是( )
A.妈妈在超市购买物品共需a元,结账时买塑料袋又花了0.3元,妈妈共花了多少元
B.一个长方形的长是a米,宽是0.3a米,这个长方形的周长是多少米
C.小明骑自行车以a千米/小时的速度行驶0.3a小时后,所行驶的路程是多少千米
D.一套商品房原价为a万元,现提价30%,那么现在的售价是多少万元
a+0.3
D
03
典例精析
2(a+0.3a)=2.6a
0.3a2
课后总结
用字母表示数的注意事项:
下节课还会继续补充和强调哦~
注意1:数与字母相乘时,若出现乘号,通常写作“·”或省略不写,且数写在字母前。
注意2:含有字母的式子用“+”或“-”连接时,后面有单位,要用“( )”将这个式子括起来。
注意3:除法一般写成分数形式。
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
