4.2 一次函数与正比例函数 课件(23张PPT)
文档属性
| 名称 | 4.2 一次函数与正比例函数 课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 09:38:59 | ||
图片预览







文档简介
(共23张PPT)
北师大版 数学 八年级上册
第四章 一次函数
2 一次函数与正比例函数
学习目标
1.理解一次函数和正比例函数的概念,能辨别一次函数与正比例函数的区别与联系;(重点)
2.能根据所给条件写出简单的一次函数表达式;(难点)
3.经历从实际问题中得到函数关系这一过程,发展抽象思维能力和数学应用能力。
复习回顾
1.函数的概念是什么?
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量.
2.表示函数的方法一般有: 、 、 .
图象法 列表法 关系式法
x≥2
一、创设情境,引入新知
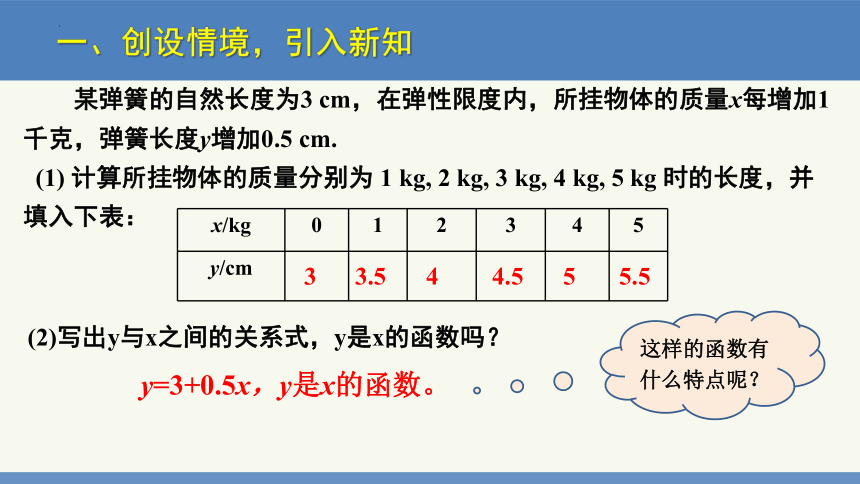
(2)写出y与x之间的关系式,y是x的函数吗?
y=3+0.5x,y是x的函数。
某弹簧的自然长度为3 cm,在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加0.5 cm.
(1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg, 5 kg 时的长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm
3
3.5
4
4.5
5
5.5
这样的函数有什么特点呢?
二、自主合作,探究新知
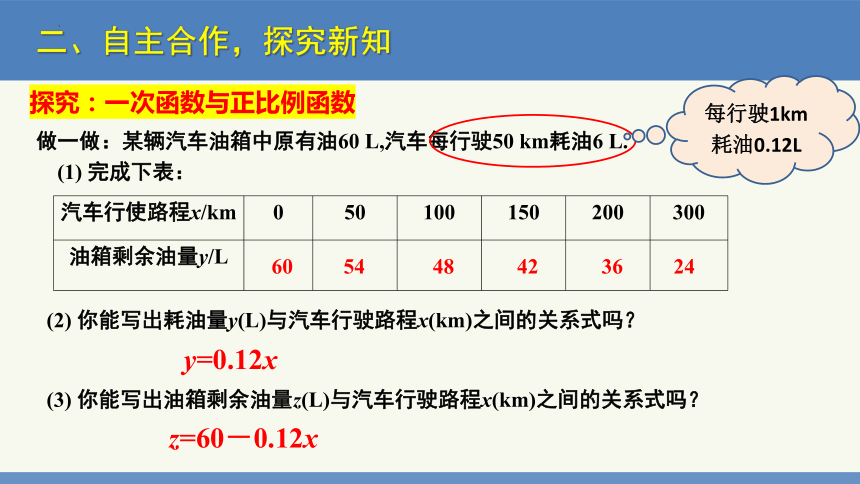
做一做:某辆汽车油箱中原有油60 L,汽车每行驶50 km耗油6 L.
(1) 完成下表:
汽车行使路程x/km 0 50 100 150 200 300
油箱剩余油量y/L
60
54
48
42
36
24
(3) 你能写出油箱剩余油量z(L)与汽车行驶路程x(km)之间的关系式吗?
z=60-0.12x
(2) 你能写出耗油量y(L)与汽车行驶路程x(km)之间的关系式吗?
y=0.12x
每行驶1km耗油0.12L
二、自主合作,探究新知
观察上面的三个函数关系式:
(1)y=3+0.5x
(2) y=0.12x
(3) z=60-0.12x
讨论一下这三个函数关系式有什么共同点
(1)都是含有两个变量的等式;
(2)变量的次数都是一次;
(3)自变量x的系数都不为0.
共同特点:
二、自主合作,探究新知
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称 y是x的一次函数.
特别地,当b=0时,称y是x的正比例函数.
一次函数的结构特征:(1) k≠0;
(2) 自变量x的次数是1;
(3) 常数项b可以为一切实数.
知识要点
即y=kx(k为常数,且k≠0)
注意:正比例函数是一种特殊的一次函数,但一次函数不一定是正比例函数。
二、自主合作,探究新知
解:⑥∵y=8x2+x(1-8x)=8x2+x-8x2=x,
∴⑥是一次函数,也是正比例函数.
跟踪练习
①③④⑥
③④⑥
注意:判断一个函数是否是一次函数,必须将其化成最简形式。
二、自主合作,探究新知
例1:写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程为y(km)与行驶时间x(h)之间的关系;
解:由路程=速度×时间,得y=60x ,y是x的 一次函数,也是x的正比例函数.
解:由圆的面积公式,得y=πx2,
y不是x的正比例函数,也不是x的一次函数.
(2)圆的面积y (cm2 )与它的半径x (cm)之间的关系.
典型例题
二、自主合作,探究新知
解:这个水池每时增加5m3水,x h增加5x m3水,
因而 y=5x+15,
y是x的一次函数,但不是x的正比例函数.
(3)某水池有水15m3,现打开进水管进水,进水速度为5m3/h,x h后这个水池有水y m3.
二、自主合作,探究新知
列一次函数关系式的步骤:
(1)寻找等量关系,可以直接将公式当做等量关系;
(2)用字母表示自变量及函数,根据等量关系列出等式;
(3)将等式变形,写成一次函数的一般形式.
知识要点
注意:对于实际问题,还要考虑自变量的取值要使实际问题有意义.
二、自主合作,探究新知
例2:自2019年1月1日起,我国居民个人劳务报酬所得税预扣预缴税款的计算方法是:每次收入不超过800元预扣预缴税款为0;每次收入超过800元但不超过4000元的,预扣预缴税款=(每日收入-800)×20%;……如某人取得劳务报酬2000元,他这笔所得应预扣预缴税款(2000-800)×20%=240(元).
(1)当每次收入超过800元但不超过4000元的,写出劳务报酬所得税预扣预缴税款y(元)与每次收入x(元)之间的关系式.
解: (1)y=(x-800)×20%=0.2x-160 (800典型例题
二、自主合作,探究新知
(2)某人某次取得劳务报酬3500元,他这笔所得应预扣预缴税款多少元?
解:当x=3500时,y=0.2×3500-160=540(元).
解:∵(4000-800)×20%=640,且 600<640
∴此人劳务报酬不超过4000元.
(3)如果某人某次预扣预缴劳务报酬所得税600元,那么此人这次取得的劳务报酬是多少元?
设此人这次取得的劳务报酬是x元,则
600=0.2x-160
解得 x=3800.
答:此人这次取得的劳务报酬是3800元.
三、即学即练,应用知识
1.下列y与x 是一次函数关系的有( )
①汽车以60 km/h 的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
②圆的面积y(cm2)与它的半径x(cm)之间的关系;
③一棵小树现在高50 cm,每个月长高2cm,x个月后这棵树的高度为ycm,y与 关系;
④某种大米的单价是 2.2 元/千克,当购买大米x 千克时,花费y元,y与x的关系.
A.1个 B.4个 C.3个 D.2个
B
C
3. 若y=(m-3)x|m|-2+m+n是y关于x的一次函数,则m= ;若它为正比例函数,则m= ,n= .
三、即学即练,应用知识
-3
-3
3
4.一位卖报人每天从报社固定购买 100 份报纸,每份进价0.6 元,然后以每份1元的价格出售。如果报纸卖不完退回报社,退回的报纸报社只按进价的 50%退款给他.如果某一天卖报人卖出的报纸为x份,所获得的利润为y元,试写出y与x 之间的关系式 .
y=0.7x-30
三、即学即练,应用知识
5.如图,甲、乙两地相距100 km,现有一列火从乙地出发,以80 km/h 的度向丙地行驶.
设x(h)表示火车行驶的时间,y(km)表示火与甲地的距离.
(1)写出y与x之间的关系式,并判断y是否为x的一次函数;
(2)当x=0.5时,求y的值.
解:(1)根据题意得y=80x+100,
∴y是x的一次函数.
(2)当x=0.5时,y=100+80×0.5=140 km/h
四、课堂小结
一次函数与正比例函数
一次函数
正比例函数
列一次函数关系式
形如y=kx+b(k,b为常数,k≠0)的函数.
形如y=kx(k为常数,且k≠0)的函数.
特例
b=0
(1)找等量关系;
(2)用字母列出等式;
(3)将等式变形成一次函数的一般形式.
五、当堂达标检测
1.下列式子中,表示y是x的正比例函数的是( )
A.y=x-1 B.y=2x C.y=2x2 D.y2=2x
B
C
五、当堂达标检测
3.下列说法中,正确的个数是( )
①正比例函数一定是一次函数;②一次函数一定是正比例函数;③速度一定时,路程s是时间t的一次函数;④圆的面积S是圆的半径r的正比例函数。
A.1 B.2 C.3 D.4
B
B
五、当堂达标检测
④
D
五、当堂达标检测
7.一次函数y =2(x+1)-3x 的常数项b= .
8.已知函数y=(k+1)x+k2-1,当k 时,它是一次函数;当k 时,它是正比例函数.
9.某音像公司对外出租光盘的收费方法:每张光盘出租后的前2天每天收费0.8元,以后每天收费0.5元那么一张光盘在出租后第n天(n>2且n为整数)与应收费y元的函数关系式为 ,若这个函数是一次函数,则自变量的取值范围是 .
2
≠-1
=1
y=0.5n+0.6
n>2且n为整数
五、当堂达标检测
10.为了增强居民节约用水的意识,某市制定了新的水费标准:每户每月用水量不超过 5 吨的部分,自来水公司按每吨2元收费;超过5吨的部分,按每吨2.6元收费.设某用户月用水量为x吨,自来水公司应收水费y元.
(1)试写出y(元)与x(吨)之间的函数关系式;
(2)某用户今年 5月份的用水量为8吨,自来水公司应收水费多少元
解:(1)当0≤x≤5时,y=2x;
当x>5时,y=10+(x-5)×2.6=2.6x-3.
(2)因为x=8>5,所以y=2.6×8-3=17.8.
答:自来水公司应收水费17.8元.
教材习题4.2;
六、布置作业
北师大版 数学 八年级上册
第四章 一次函数
2 一次函数与正比例函数
学习目标
1.理解一次函数和正比例函数的概念,能辨别一次函数与正比例函数的区别与联系;(重点)
2.能根据所给条件写出简单的一次函数表达式;(难点)
3.经历从实际问题中得到函数关系这一过程,发展抽象思维能力和数学应用能力。
复习回顾
1.函数的概念是什么?
一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有唯一的值与它对应,那么我们称y是x的函数,其中x是自变量.
2.表示函数的方法一般有: 、 、 .
图象法 列表法 关系式法
x≥2
一、创设情境,引入新知
(2)写出y与x之间的关系式,y是x的函数吗?
y=3+0.5x,y是x的函数。
某弹簧的自然长度为3 cm,在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加0.5 cm.
(1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg, 5 kg 时的长度,并填入下表:
x/kg 0 1 2 3 4 5
y/cm
3
3.5
4
4.5
5
5.5
这样的函数有什么特点呢?
二、自主合作,探究新知
做一做:某辆汽车油箱中原有油60 L,汽车每行驶50 km耗油6 L.
(1) 完成下表:
汽车行使路程x/km 0 50 100 150 200 300
油箱剩余油量y/L
60
54
48
42
36
24
(3) 你能写出油箱剩余油量z(L)与汽车行驶路程x(km)之间的关系式吗?
z=60-0.12x
(2) 你能写出耗油量y(L)与汽车行驶路程x(km)之间的关系式吗?
y=0.12x
每行驶1km耗油0.12L
二、自主合作,探究新知
观察上面的三个函数关系式:
(1)y=3+0.5x
(2) y=0.12x
(3) z=60-0.12x
讨论一下这三个函数关系式有什么共同点
(1)都是含有两个变量的等式;
(2)变量的次数都是一次;
(3)自变量x的系数都不为0.
共同特点:
二、自主合作,探究新知
若两个变量 x、y之间的关系可以表示成y=kx+b(k,b为常数,k≠0)的形式,则称 y是x的一次函数.
特别地,当b=0时,称y是x的正比例函数.
一次函数的结构特征:(1) k≠0;
(2) 自变量x的次数是1;
(3) 常数项b可以为一切实数.
知识要点
即y=kx(k为常数,且k≠0)
注意:正比例函数是一种特殊的一次函数,但一次函数不一定是正比例函数。
二、自主合作,探究新知
解:⑥∵y=8x2+x(1-8x)=8x2+x-8x2=x,
∴⑥是一次函数,也是正比例函数.
跟踪练习
①③④⑥
③④⑥
注意:判断一个函数是否是一次函数,必须将其化成最简形式。
二、自主合作,探究新知
例1:写出下列各题中y与 x之间的关系式,并判断:y是否为x的一次函数?是否为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程为y(km)与行驶时间x(h)之间的关系;
解:由路程=速度×时间,得y=60x ,y是x的 一次函数,也是x的正比例函数.
解:由圆的面积公式,得y=πx2,
y不是x的正比例函数,也不是x的一次函数.
(2)圆的面积y (cm2 )与它的半径x (cm)之间的关系.
典型例题
二、自主合作,探究新知
解:这个水池每时增加5m3水,x h增加5x m3水,
因而 y=5x+15,
y是x的一次函数,但不是x的正比例函数.
(3)某水池有水15m3,现打开进水管进水,进水速度为5m3/h,x h后这个水池有水y m3.
二、自主合作,探究新知
列一次函数关系式的步骤:
(1)寻找等量关系,可以直接将公式当做等量关系;
(2)用字母表示自变量及函数,根据等量关系列出等式;
(3)将等式变形,写成一次函数的一般形式.
知识要点
注意:对于实际问题,还要考虑自变量的取值要使实际问题有意义.
二、自主合作,探究新知
例2:自2019年1月1日起,我国居民个人劳务报酬所得税预扣预缴税款的计算方法是:每次收入不超过800元预扣预缴税款为0;每次收入超过800元但不超过4000元的,预扣预缴税款=(每日收入-800)×20%;……如某人取得劳务报酬2000元,他这笔所得应预扣预缴税款(2000-800)×20%=240(元).
(1)当每次收入超过800元但不超过4000元的,写出劳务报酬所得税预扣预缴税款y(元)与每次收入x(元)之间的关系式.
解: (1)y=(x-800)×20%=0.2x-160 (800
二、自主合作,探究新知
(2)某人某次取得劳务报酬3500元,他这笔所得应预扣预缴税款多少元?
解:当x=3500时,y=0.2×3500-160=540(元).
解:∵(4000-800)×20%=640,且 600<640
∴此人劳务报酬不超过4000元.
(3)如果某人某次预扣预缴劳务报酬所得税600元,那么此人这次取得的劳务报酬是多少元?
设此人这次取得的劳务报酬是x元,则
600=0.2x-160
解得 x=3800.
答:此人这次取得的劳务报酬是3800元.
三、即学即练,应用知识
1.下列y与x 是一次函数关系的有( )
①汽车以60 km/h 的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系;
②圆的面积y(cm2)与它的半径x(cm)之间的关系;
③一棵小树现在高50 cm,每个月长高2cm,x个月后这棵树的高度为ycm,y与 关系;
④某种大米的单价是 2.2 元/千克,当购买大米x 千克时,花费y元,y与x的关系.
A.1个 B.4个 C.3个 D.2个
B
C
3. 若y=(m-3)x|m|-2+m+n是y关于x的一次函数,则m= ;若它为正比例函数,则m= ,n= .
三、即学即练,应用知识
-3
-3
3
4.一位卖报人每天从报社固定购买 100 份报纸,每份进价0.6 元,然后以每份1元的价格出售。如果报纸卖不完退回报社,退回的报纸报社只按进价的 50%退款给他.如果某一天卖报人卖出的报纸为x份,所获得的利润为y元,试写出y与x 之间的关系式 .
y=0.7x-30
三、即学即练,应用知识
5.如图,甲、乙两地相距100 km,现有一列火从乙地出发,以80 km/h 的度向丙地行驶.
设x(h)表示火车行驶的时间,y(km)表示火与甲地的距离.
(1)写出y与x之间的关系式,并判断y是否为x的一次函数;
(2)当x=0.5时,求y的值.
解:(1)根据题意得y=80x+100,
∴y是x的一次函数.
(2)当x=0.5时,y=100+80×0.5=140 km/h
四、课堂小结
一次函数与正比例函数
一次函数
正比例函数
列一次函数关系式
形如y=kx+b(k,b为常数,k≠0)的函数.
形如y=kx(k为常数,且k≠0)的函数.
特例
b=0
(1)找等量关系;
(2)用字母列出等式;
(3)将等式变形成一次函数的一般形式.
五、当堂达标检测
1.下列式子中,表示y是x的正比例函数的是( )
A.y=x-1 B.y=2x C.y=2x2 D.y2=2x
B
C
五、当堂达标检测
3.下列说法中,正确的个数是( )
①正比例函数一定是一次函数;②一次函数一定是正比例函数;③速度一定时,路程s是时间t的一次函数;④圆的面积S是圆的半径r的正比例函数。
A.1 B.2 C.3 D.4
B
B
五、当堂达标检测
④
D
五、当堂达标检测
7.一次函数y =2(x+1)-3x 的常数项b= .
8.已知函数y=(k+1)x+k2-1,当k 时,它是一次函数;当k 时,它是正比例函数.
9.某音像公司对外出租光盘的收费方法:每张光盘出租后的前2天每天收费0.8元,以后每天收费0.5元那么一张光盘在出租后第n天(n>2且n为整数)与应收费y元的函数关系式为 ,若这个函数是一次函数,则自变量的取值范围是 .
2
≠-1
=1
y=0.5n+0.6
n>2且n为整数
五、当堂达标检测
10.为了增强居民节约用水的意识,某市制定了新的水费标准:每户每月用水量不超过 5 吨的部分,自来水公司按每吨2元收费;超过5吨的部分,按每吨2.6元收费.设某用户月用水量为x吨,自来水公司应收水费y元.
(1)试写出y(元)与x(吨)之间的函数关系式;
(2)某用户今年 5月份的用水量为8吨,自来水公司应收水费多少元
解:(1)当0≤x≤5时,y=2x;
当x>5时,y=10+(x-5)×2.6=2.6x-3.
(2)因为x=8>5,所以y=2.6×8-3=17.8.
答:自来水公司应收水费17.8元.
教材习题4.2;
六、布置作业
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
