4.3等可能条件下的概率(二) 课件(25张PPT)
文档属性
| 名称 | 4.3等可能条件下的概率(二) 课件(25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 09:44:05 | ||
图片预览








文档简介
(共25张PPT)
第4章 · 等可能条件下的概率
4.3 等可能条件下的概率(二)
学习目标
1. 能把“等可能条件下的概率(二)(几何概型)”转化为“等可能条件下的概率(一)(古典概型)”,并进行简单的计算;
2.感受一类事件发生的概率(能转化为古典概型的几何概型)的大小与面积大小有关.
知识回顾
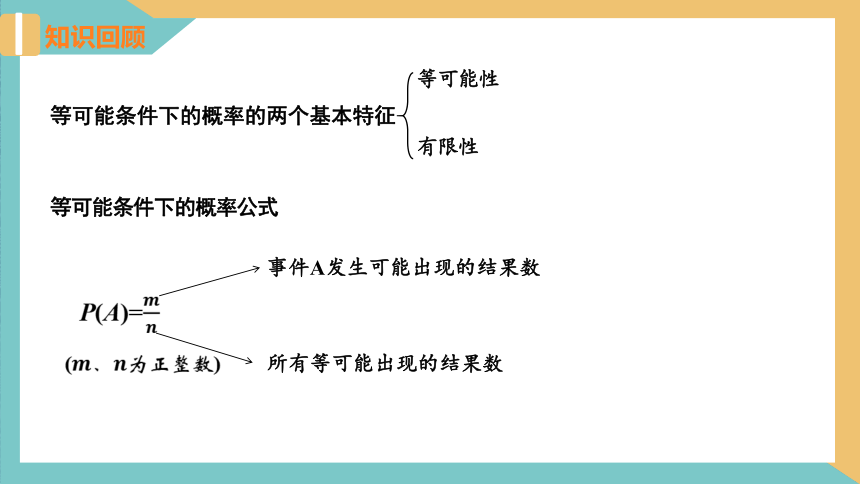
等可能条件下的概率的两个基本特征
等可能性
有限性
等可能条件下的概率公式
事件A发生可能出现的结果数
所有等可能出现的结果数
情境引入
元旦将至,某超市为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被等分为24份). 规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.
当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率有多大?
获得500元、100元、50元礼品的概率分别是多少?
超 市 抽 奖
观察与思考
1.转动如图所示的转盘,当转盘停止转动时,指针的位置有多少种可能的结果?这些结果具有等可能性吗?
有无数多种可能的结果,它们具有等可能性.
观察与思考
2.现将转盘分成8个面积相等的扇形,转动转盘,当转盘停止转动时,指针的位置有多少种可能的结果(指针指向两个扇形的交线时,当作指向右边的扇形)?这些结果具有等可能性吗?
1
2
3
4
5
6
7
8
有8种可能的结果,它们具有等可能性.
无限
有限
观察与思考
3.现将转盘涂上不同的颜色,这些扇形除颜色外都相同. 转动转盘.
8个
(1)当转盘停止转动时,指针的位置有多少种可能的结果?(指针指向两个扇形的交线时,当作指向右边的扇形)
(2)指针指向红色区域可能发生的结果数有几个?
6个
(3)怎样计算指针指向红色区域的概率?
讨论与交流
2.若要改变指针指向红色区域的概率,需要改变什么?
红色区域的面积.
3.“指针指向红色区域”与“指针不指向红色区域”这两个事件及概率之间有怎样的联系,你有何发现?
这两个事件概率之和为1.
1.你认为概率的大小与什么因素有直接关系?
概率的大小与面积的大小有关.
新知应用
元旦将至,某超市为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被等分为24份). 规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.
当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率有多大?
获得500元、100元、50元礼品的概率分别是多少?
超 市 抽 奖
解:顾客购物1400元,可以抽奖1次.
新知归纳
1.一般用阴影区域表示所求事件;
某区域的概率大小与某区域所占总面积的大小有关.
几何型概率的求法:
新知巩固
1.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,求下列事件发生的概率:
(1)指针所落扇形中的数为6;
(2)指针所落扇形中的数为偶数;
(3)指针所落扇形中的数小于4;
(4)指针所落扇形中的数不大于4;
(5)指针所落扇形中的数大于0.
新知巩固
2.如图,飞镖游戏板中每一块小正方形除颜色外都相同. 假设飞镖击中每一块小正方形是等可能的(击中小正方形的边界线或没有击中游戏板,则重投1次),任意投掷飞镖 1次,击中哪种颜色的小正方形的概率较大?为什么?
击中白色小正方形的概率较大.
3.小华训练飞镖,在木板上画了半径为20 cm和30 cm的同心圆,如图,他在距木板5米开外将一个飞镖随机投掷到该图形内,则飞镖落在阴影区域的概率为 .
新知巩固
拓展与延伸
设计一个转盘,任意转动转盘1次,当转盘停止转动时使得指针:
课堂小结
等可能条件下的概率(二)(几何概型)
等可能条件下的概率(一)(古典概型)
无限
有限
与面积大小有关
设试验结果落在某个区域S中每个点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率
当堂检测
1. 如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
A
当堂检测
A. B. C. D.
D
当堂检测
3.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A
C
B
B
当堂检测
4.如图,一块飞镖游戏板由大小相等的小等边三角形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),则击中黑色区域的概率是_______.
当堂检测
5.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是_______.
当堂检测
6. 如图,在5×6的网格飞镖游戏板中,每块小正方形除颜色外都相同.假设飞镖击中每一块小正方形是等可能的且飞镖每次都落在游戏板上,任意投掷飞镖1次,飞镖击中扇形OAB(涂色部分)的概率为_____.
A
B
O
当堂检测
7.如图,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1) 现随机转动转盘一次,停止后,指针指向1的概率为_____;
1
2
3
(2) 小明和小华利用这个转盘做游戏,游戏规则如下:随机转动转盘两次,停止后,指针各指向一个数,若两数之积为偶数,则小明胜;否则,小华胜.该游戏规则对双方公平吗?请用列表的方法说明理由.
当堂检测
解:不公平 理由:列表如下:
第一次 第二次
1 2 3
1 1 2 3
2 2 4 6
3 3 6 9
当堂检测
A
B
①
B
C
A
②
(1)向圆形靶子掷一枚飞镖,投到A,B,C区域的概率分别是多少?
当堂检测
(2) 向两个靶子各掷一枚飞镖,投到同一名称区域的概率是多少?
解:把圆形靶子中的A区域等分为2个区域A1、A2:
向①投飞镖 向②投飞镖
A1 A2 B C
A AA1 AA2 AB AC
B BA1 BA2 BB BC
C CA1 CA2 CB CC
第4章 · 等可能条件下的概率
4.3 等可能条件下的概率(二)
学习目标
1. 能把“等可能条件下的概率(二)(几何概型)”转化为“等可能条件下的概率(一)(古典概型)”,并进行简单的计算;
2.感受一类事件发生的概率(能转化为古典概型的几何概型)的大小与面积大小有关.
知识回顾
等可能条件下的概率的两个基本特征
等可能性
有限性
等可能条件下的概率公式
事件A发生可能出现的结果数
所有等可能出现的结果数
情境引入
元旦将至,某超市为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被等分为24份). 规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.
当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率有多大?
获得500元、100元、50元礼品的概率分别是多少?
超 市 抽 奖
观察与思考
1.转动如图所示的转盘,当转盘停止转动时,指针的位置有多少种可能的结果?这些结果具有等可能性吗?
有无数多种可能的结果,它们具有等可能性.
观察与思考
2.现将转盘分成8个面积相等的扇形,转动转盘,当转盘停止转动时,指针的位置有多少种可能的结果(指针指向两个扇形的交线时,当作指向右边的扇形)?这些结果具有等可能性吗?
1
2
3
4
5
6
7
8
有8种可能的结果,它们具有等可能性.
无限
有限
观察与思考
3.现将转盘涂上不同的颜色,这些扇形除颜色外都相同. 转动转盘.
8个
(1)当转盘停止转动时,指针的位置有多少种可能的结果?(指针指向两个扇形的交线时,当作指向右边的扇形)
(2)指针指向红色区域可能发生的结果数有几个?
6个
(3)怎样计算指针指向红色区域的概率?
讨论与交流
2.若要改变指针指向红色区域的概率,需要改变什么?
红色区域的面积.
3.“指针指向红色区域”与“指针不指向红色区域”这两个事件及概率之间有怎样的联系,你有何发现?
这两个事件概率之和为1.
1.你认为概率的大小与什么因素有直接关系?
概率的大小与面积的大小有关.
新知应用
元旦将至,某超市为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被等分为24份). 规定:顾客每购满1000元的商品,可获得一次转动转盘的机会.
当转盘停止转动时,指针指向红、蓝、黄区域,顾客可分别获得500元、100元、50元的礼品.某顾客购物1400元,他获得礼品的概率有多大?
获得500元、100元、50元礼品的概率分别是多少?
超 市 抽 奖
解:顾客购物1400元,可以抽奖1次.
新知归纳
1.一般用阴影区域表示所求事件;
某区域的概率大小与某区域所占总面积的大小有关.
几何型概率的求法:
新知巩固
1.如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,求下列事件发生的概率:
(1)指针所落扇形中的数为6;
(2)指针所落扇形中的数为偶数;
(3)指针所落扇形中的数小于4;
(4)指针所落扇形中的数不大于4;
(5)指针所落扇形中的数大于0.
新知巩固
2.如图,飞镖游戏板中每一块小正方形除颜色外都相同. 假设飞镖击中每一块小正方形是等可能的(击中小正方形的边界线或没有击中游戏板,则重投1次),任意投掷飞镖 1次,击中哪种颜色的小正方形的概率较大?为什么?
击中白色小正方形的概率较大.
3.小华训练飞镖,在木板上画了半径为20 cm和30 cm的同心圆,如图,他在距木板5米开外将一个飞镖随机投掷到该图形内,则飞镖落在阴影区域的概率为 .
新知巩固
拓展与延伸
设计一个转盘,任意转动转盘1次,当转盘停止转动时使得指针:
课堂小结
等可能条件下的概率(二)(几何概型)
等可能条件下的概率(一)(古典概型)
无限
有限
与面积大小有关
设试验结果落在某个区域S中每个点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率
当堂检测
1. 如图所示的是由8个全等的小正方形组成的图案,假设可以随意在图中取一点,那么这个点取在阴影部分的概率是( )
A
当堂检测
A. B. C. D.
D
当堂检测
3.如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=13,AC=5,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
A
C
B
B
当堂检测
4.如图,一块飞镖游戏板由大小相等的小等边三角形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),则击中黑色区域的概率是_______.
当堂检测
5.一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上,每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是_______.
当堂检测
6. 如图,在5×6的网格飞镖游戏板中,每块小正方形除颜色外都相同.假设飞镖击中每一块小正方形是等可能的且飞镖每次都落在游戏板上,任意投掷飞镖1次,飞镖击中扇形OAB(涂色部分)的概率为_____.
A
B
O
当堂检测
7.如图,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
(1) 现随机转动转盘一次,停止后,指针指向1的概率为_____;
1
2
3
(2) 小明和小华利用这个转盘做游戏,游戏规则如下:随机转动转盘两次,停止后,指针各指向一个数,若两数之积为偶数,则小明胜;否则,小华胜.该游戏规则对双方公平吗?请用列表的方法说明理由.
当堂检测
解:不公平 理由:列表如下:
第一次 第二次
1 2 3
1 1 2 3
2 2 4 6
3 3 6 9
当堂检测
A
B
①
B
C
A
②
(1)向圆形靶子掷一枚飞镖,投到A,B,C区域的概率分别是多少?
当堂检测
(2) 向两个靶子各掷一枚飞镖,投到同一名称区域的概率是多少?
解:把圆形靶子中的A区域等分为2个区域A1、A2:
向①投飞镖 向②投飞镖
A1 A2 B C
A AA1 AA2 AB AC
B BA1 BA2 BB BC
C CA1 CA2 CB CC
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
