13.1.2线段的垂直平分线的性质(第1课时) 课件(36张PPT)
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质(第1课时) 课件(36张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览









文档简介
(共36张PPT)
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十三章轴对称
13.1.2线段的垂直平分线的性质(第1课时)
学习目标
1.探索并证明线段垂直平分线的性质定理和判定定理.
2.熟练运用线段垂直平分线的性质和判定解决实际问题.
复习提问
1.什么叫线段垂直平分线?
2.什么叫轴对称图形?
3.线段是轴对称图形吗?若是,指出它的对称轴;若不是,说明理由.
探究新知
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
探究
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
由此你能得到什么结论?
探究新知
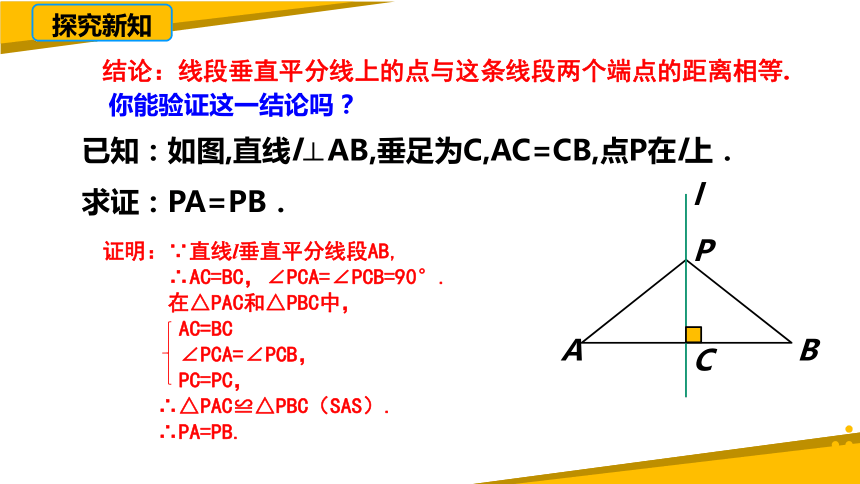
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上.
求证:PA=PB.
P
A
B
l
C
证明:∵直线l垂直平分线段AB,
∴AC=BC,∠PCA=∠PCB=90°.
在△PAC和△PBC中,
AC=BC
∠PCA=∠PCB,
PC=PC,
∴△PAC≌△PBC(SAS).
∴PA=PB.
建立模型
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l⊥AB,AC=BC,
∴PA=PB.
A
B
l
┐
C
P
符号语言表示:
线段的垂直平分线的性质:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
探究新知
A
B
l
┐
C
P
已知:点P是线段AB外任意一点,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为C.
∵l⊥AB,
∴∠PCA=∠PCB=90°,
在Rt△PAC和Rt△PBC中,
PA=PB,
PC=PC,
∴Rt△PAC≌Rt△PBC(HL)
∴AC=BC.
∵∠PCA=∠PCB=90°,
∴P在线段AB的垂直平分线上.
你能得出什么结论呢?
建立模型
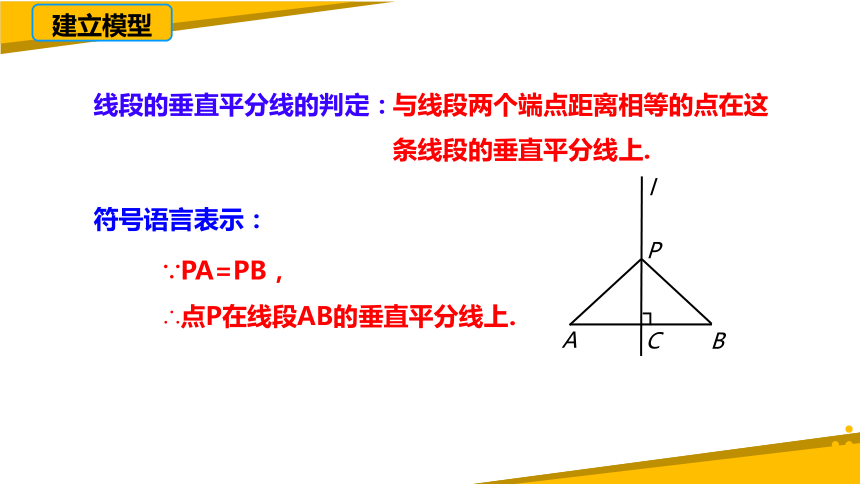
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵PA=PB,
∴点P在线段AB的垂直平分线上.
符号语言表示:
线段的垂直平分线的判定:
A
B
l
┐
C
P
探究新知
1.从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2.反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
C
P
典例解析
例1.尺规作图,经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
B
.
探究新知
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
K
A
B
C
D
E
探究新知
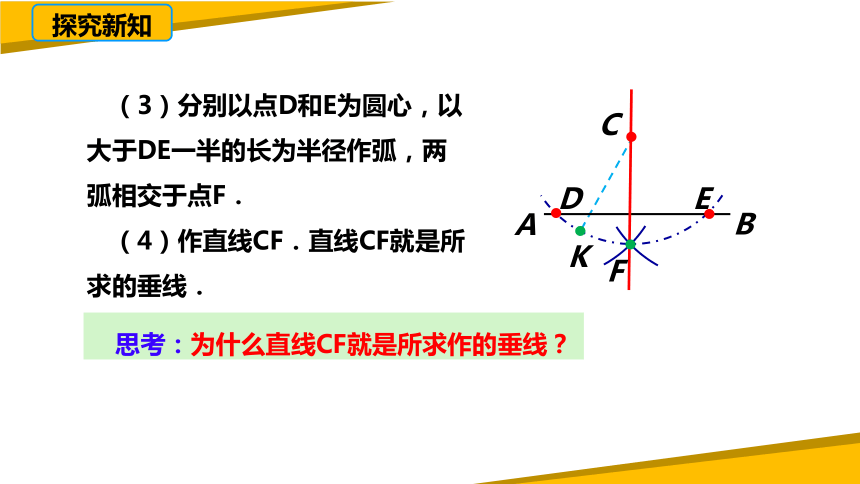
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
思考:为什么直线CF就是所求作的垂线?
探究新知
∵从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F都在DE的垂直平分线上.
∴CF就是线段DE的垂直平分线.
∵点D,E在直线AB上,
∴CF就是所求直线AB的垂线.
A
B
C
D
E
F
归纳总结
1.要作出线段的垂直平分线,必须找到两个与线段两个端点距离相等的点,才能确定已知线段的垂直平分线.
2.证明一条直线是线段的垂直平分线时,必须证明两个点在线段的垂直平分线上.
典例解析
例1.如图, 已知△ABC中,BC=7,AB的垂直平分线交AB于E,交AC于D, △BCD的周长为19,求AC的长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC=19
∵BC=7
∴ BD+DC +7=19
∴ BD+DC =19-7=12.
∴ AD+DC =12.
∴AC=12
典例解析
例2:已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上.
B
A
C
M
N
E
F
P
证明:∵点P在线段AB的垂直平分线MN上,
结论:三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
∴PA=PB.
同理可得:PB=PC.
∴PA=PC.
∴点P在线段AC的垂直平分线上
随堂练习
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
随堂练习
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
随堂练习
随堂练习
4.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,△ABC的周长是17cm,求AC的长.
中考链接
C
中考链接
D
中考链接
B
课堂小结
线段的垂直平分
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
当堂测试
B
D
当堂测试
B
B
当堂测试
A
当堂测试
C
A
分层作业
D
A
分层作业
B
B
分层作业
C
C
分层作业
B
分层作业
B
分层作业
C
分层作业
D
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十三章轴对称
13.1.2线段的垂直平分线的性质(第1课时)
学习目标
1.探索并证明线段垂直平分线的性质定理和判定定理.
2.熟练运用线段垂直平分线的性质和判定解决实际问题.
复习提问
1.什么叫线段垂直平分线?
2.什么叫轴对称图形?
3.线段是轴对称图形吗?若是,指出它的对称轴;若不是,说明理由.
探究新知
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
探究
如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
由此你能得到什么结论?
探究新知
结论:线段垂直平分线上的点与这条线段两个端点的距离相等.
你能验证这一结论吗?
已知:如图,直线l⊥AB,垂足为C,AC=CB,点P在l上.
求证:PA=PB.
P
A
B
l
C
证明:∵直线l垂直平分线段AB,
∴AC=BC,∠PCA=∠PCB=90°.
在△PAC和△PBC中,
AC=BC
∠PCA=∠PCB,
PC=PC,
∴△PAC≌△PBC(SAS).
∴PA=PB.
建立模型
线段垂直平分线上的点与这条线段两个端点的距离相等.
∵直线l⊥AB,AC=BC,
∴PA=PB.
A
B
l
┐
C
P
符号语言表示:
线段的垂直平分线的性质:
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
探究新知
A
B
l
┐
C
P
已知:点P是线段AB外任意一点,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:过点P作直线l,使得l⊥AB,垂足为C.
∵l⊥AB,
∴∠PCA=∠PCB=90°,
在Rt△PAC和Rt△PBC中,
PA=PB,
PC=PC,
∴Rt△PAC≌Rt△PBC(HL)
∴AC=BC.
∵∠PCA=∠PCB=90°,
∴P在线段AB的垂直平分线上.
你能得出什么结论呢?
建立模型
与线段两个端点距离相等的点在这条线段的垂直平分线上.
∵PA=PB,
∴点P在线段AB的垂直平分线上.
符号语言表示:
线段的垂直平分线的判定:
A
B
l
┐
C
P
探究新知
1.从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等.
2.反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
C
P
典例解析
例1.尺规作图,经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.求作:AB的垂线,使它经过点C.
A
B
B
.
探究新知
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.
K
A
B
C
D
E
探究新知
(3)分别以点D和E为圆心,以大于DE一半的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求的垂线.
K
A
B
C
D
E
F
思考:为什么直线CF就是所求作的垂线?
探究新知
∵从作法的(2)(3)步可知CD=CE,DF=EF,
∴点C,F都在DE的垂直平分线上.
∴CF就是线段DE的垂直平分线.
∵点D,E在直线AB上,
∴CF就是所求直线AB的垂线.
A
B
C
D
E
F
归纳总结
1.要作出线段的垂直平分线,必须找到两个与线段两个端点距离相等的点,才能确定已知线段的垂直平分线.
2.证明一条直线是线段的垂直平分线时,必须证明两个点在线段的垂直平分线上.
典例解析
例1.如图, 已知△ABC中,BC=7,AB的垂直平分线交AB于E,交AC于D, △BCD的周长为19,求AC的长.
∴BD=AD,
A
B
C
D
E
解:∵ED是线段AB的垂直平分线,
∵ △BCD的周长=BD+DC+BC=19
∵BC=7
∴ BD+DC +7=19
∴ BD+DC =19-7=12.
∴ AD+DC =12.
∴AC=12
典例解析
例2:已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.
求证:点P在AC的垂直平分线上.
B
A
C
M
N
E
F
P
证明:∵点P在线段AB的垂直平分线MN上,
结论:三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
∴PA=PB.
同理可得:PB=PC.
∴PA=PC.
∴点P在线段AC的垂直平分线上
随堂练习
1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上.AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
随堂练习
2.如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
随堂练习
随堂练习
4.如图所示,在△ABC中,AC的垂直平分线交AC于E,交BC于D,
△ABD的周长为12cm,AC=5cm,△ABC的周长是17cm,求AC的长.
中考链接
C
中考链接
D
中考链接
B
课堂小结
线段的垂直平分
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
当堂测试
B
D
当堂测试
B
B
当堂测试
A
当堂测试
C
A
分层作业
D
A
分层作业
B
B
分层作业
C
C
分层作业
B
分层作业
B
分层作业
C
分层作业
D
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
