13.1.2线段的垂直平分线的性质(第2课时) 课件(21张PPT)
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质(第2课时) 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 10:16:43 | ||
图片预览








文档简介
(共21张PPT)
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十三章轴对称
13.1.2线段的垂直平分线的性质(第2课时)
学习目标
1.能用尺规作图作一条线段的垂直平分线.
2.能正确找出轴对称图形的对称轴.
3.熟练运用线段垂直平分线的性质和判定解决实际问题.
复习提问
1.什么叫线段的垂直平分线?
2. 线段垂直平分线的性质?
3.线段垂直平分线的判定?
探究新知
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方
A
B
探究新知
思考:
直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
探究新知
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
探究新知
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
根据上面例题,你能概括出作对称轴的步骤吗?
探究新知
A
B
公共汽车站
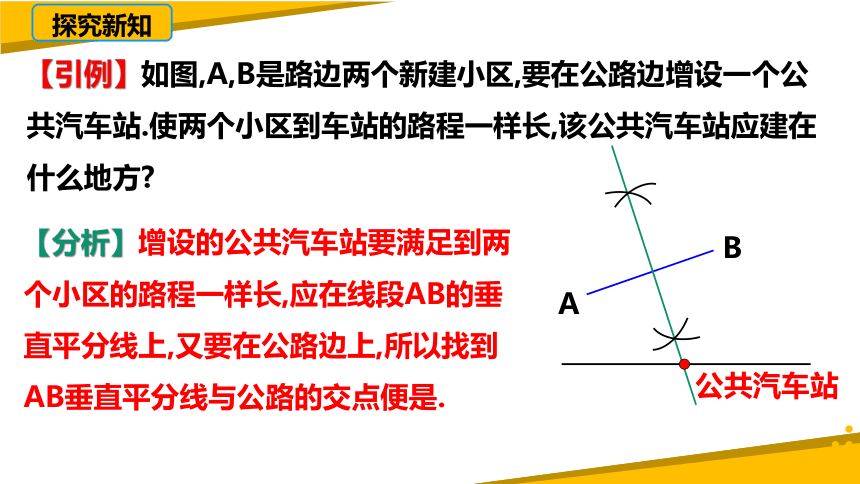
【引例】如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方
【分析】增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
探究新知
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
注意:找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
探究新知
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
类似的,请你尝试动手作出这个五角星的其他对称轴.
典例解析
例1.如图,在公路MN和公路PQ之间有两个村庄A、B,现要修建一座仓库,使仓库到两条公路和两村庄的距离分别相等,请在图上画出仓库应建在何处,并说明理由(只保留作图痕迹,不写作法).
解:如图,点O即为仓库所建位置,
理由如下:
∵O到A、B距离相等
∴0在AB的垂直平分线上
∵O到公路的距离相等
∴O在两条公路相交形成的角的平分线上
因而O为AB垂直平分线与∠DCE的平分线的交点.
典例解析
例2.如图,在△ABC中,AB=BC=6cm,AC=4cm.
(1)作BC的垂直平分线MN,垂足为N,交AB于点M;
(2)在(1)的条件下,连接MC,求△AMC的周长.
解:(1)如图所示,MN为所求的直线.
(2)连接MC
∵MN是BC的垂直平分线..
∴BM=CM.
∴C△AMC=AM+MC+AC=AM+BM+AC
=AB+AC=6+4=10(cm)
随堂练习
1.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
随堂练习
角是轴对称图形,角平分线所在的直线就是角的对称轴.
2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
随堂练习
3.如图,与图形 A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
随堂练习
4.如图,在△ABC中,AB = AC,∠A = 120°, AB的垂直平分线交BC于D,求证:CD =2BD.
证明:连结AD
∵D在AB垂直平分线上
∴BD=AD
∴∠B=∠BAD
∵∠BAC=120° AB=AC
∴∠B=∠C=30°
∴∠DAC=90°
在Rt△DAC中 ∵∠C=30° ∴DC=2AD即DC=2BD.
中考链接
C
中考链接
D
中考链接
B
课堂小结
线段的垂直
平分线的
有关作图
尺规作图
作对称轴的常见方法
属于基本作图之一,必须熟熟练掌握
(1)将图形对折;
(2)用尺规作图;
(3)用刻度尺先取一对对称点连线的中点,然后作垂线
作轴对称图形对称轴的步骤
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 八年级上册
2023-2024学年度上学期人教版精品课件
第十三章轴对称
13.1.2线段的垂直平分线的性质(第2课时)
学习目标
1.能用尺规作图作一条线段的垂直平分线.
2.能正确找出轴对称图形的对称轴.
3.熟练运用线段垂直平分线的性质和判定解决实际问题.
复习提问
1.什么叫线段的垂直平分线?
2. 线段垂直平分线的性质?
3.线段垂直平分线的判定?
探究新知
如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站,使两个小区到车站的路程一样长,该公共汽车站应建在什么地方
A
B
探究新知
思考:
直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
探究新知
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
A
B
探究新知
例2.如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
作法:如图所示:
(1)分别以点A和点B为圆心,大于 AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
A
B
根据上面例题,你能概括出作对称轴的步骤吗?
探究新知
A
B
公共汽车站
【引例】如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方
【分析】增设的公共汽车站要满足到两个小区的路程一样长,应在线段AB的垂直平分线上,又要在公路边上,所以找到AB垂直平分线与公路的交点便是.
探究新知
作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
注意:找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
探究新知
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
类似的,请你尝试动手作出这个五角星的其他对称轴.
典例解析
例1.如图,在公路MN和公路PQ之间有两个村庄A、B,现要修建一座仓库,使仓库到两条公路和两村庄的距离分别相等,请在图上画出仓库应建在何处,并说明理由(只保留作图痕迹,不写作法).
解:如图,点O即为仓库所建位置,
理由如下:
∵O到A、B距离相等
∴0在AB的垂直平分线上
∵O到公路的距离相等
∴O在两条公路相交形成的角的平分线上
因而O为AB垂直平分线与∠DCE的平分线的交点.
典例解析
例2.如图,在△ABC中,AB=BC=6cm,AC=4cm.
(1)作BC的垂直平分线MN,垂足为N,交AB于点M;
(2)在(1)的条件下,连接MC,求△AMC的周长.
解:(1)如图所示,MN为所求的直线.
(2)连接MC
∵MN是BC的垂直平分线..
∴BM=CM.
∴C△AMC=AM+MC+AC=AM+BM+AC
=AB+AC=6+4=10(cm)
随堂练习
1.作出下列图形的一条对称轴,和同学比较一下,你们作出的对称轴一样吗?
随堂练习
角是轴对称图形,角平分线所在的直线就是角的对称轴.
2.如图,角是轴对称图形吗?如果是,它的对称轴是什么?
随堂练习
3.如图,与图形 A 成轴对称的是哪个图形?画出它的对称轴.
A
B
C
D
随堂练习
4.如图,在△ABC中,AB = AC,∠A = 120°, AB的垂直平分线交BC于D,求证:CD =2BD.
证明:连结AD
∵D在AB垂直平分线上
∴BD=AD
∴∠B=∠BAD
∵∠BAC=120° AB=AC
∴∠B=∠C=30°
∴∠DAC=90°
在Rt△DAC中 ∵∠C=30° ∴DC=2AD即DC=2BD.
中考链接
C
中考链接
D
中考链接
B
课堂小结
线段的垂直
平分线的
有关作图
尺规作图
作对称轴的常见方法
属于基本作图之一,必须熟熟练掌握
(1)将图形对折;
(2)用尺规作图;
(3)用刻度尺先取一对对称点连线的中点,然后作垂线
作轴对称图形对称轴的步骤
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
