24.1.2垂直于弦的直径 课件(39张PPT)
文档属性
| 名称 | 24.1.2垂直于弦的直径 课件(39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 10:24:00 | ||
图片预览









文档简介
(共39张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
24.1.2垂直于弦的直径
学习目标
1.理解垂径定理推论;
2.能运用垂径定理及其推论解决有关问题.
复习提问
【提问】简述轴对称图形的概念?说出常见的轴对称图形?
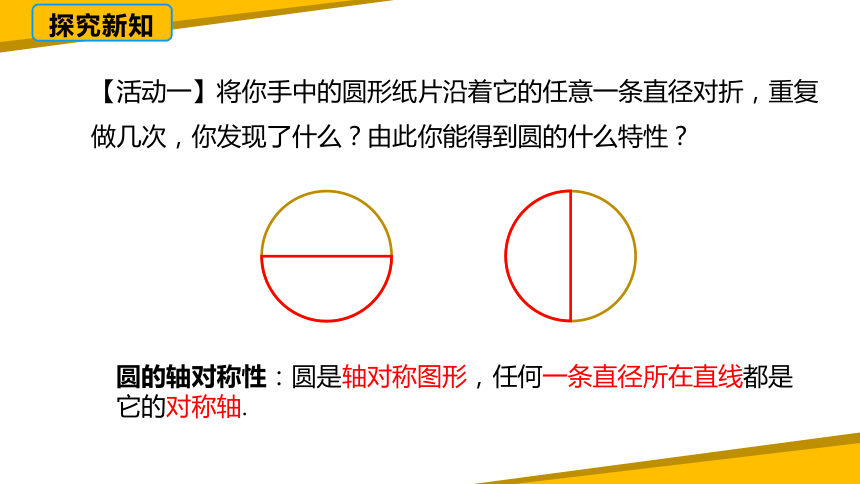
【活动一】将你手中的圆形纸片沿着它的任意一条直径对折,重复做几次,你发现了什么?由此你能得到圆的什么特性?
圆的轴对称性:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
探究新知
【活动二】在圆形纸片上作 O的任意一条弦AB, 再作直径CD⊥AB, 垂足为E.沿着直径CD对折,你发现了什么?有哪些相等的线段和弧?
探究新知
【证明一】已知:如图,CD是⊙O的任一条直径,A是⊙O上点C,D以外任意一点,过点A作CD⊥AB,交⊙O于点B,垂足为E.求证:AE=BE.
证明:连接OA、OB,
在△OAB中,
∵OA=OB ∴△OAB是等腰三角形
又∵ CD⊥AB,
∴AE=BE
即CD是AB的垂直平分线.
这就是说对于圆上任意一点A,在圆上都有关于直线CD的对称点B,因此⊙O关于直线CD对称.
探究新知
【提问】由此你觉得垂直于弦的直径有什么特点呢?
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理:
符号语言:
∵CD是直径,CD⊥AB
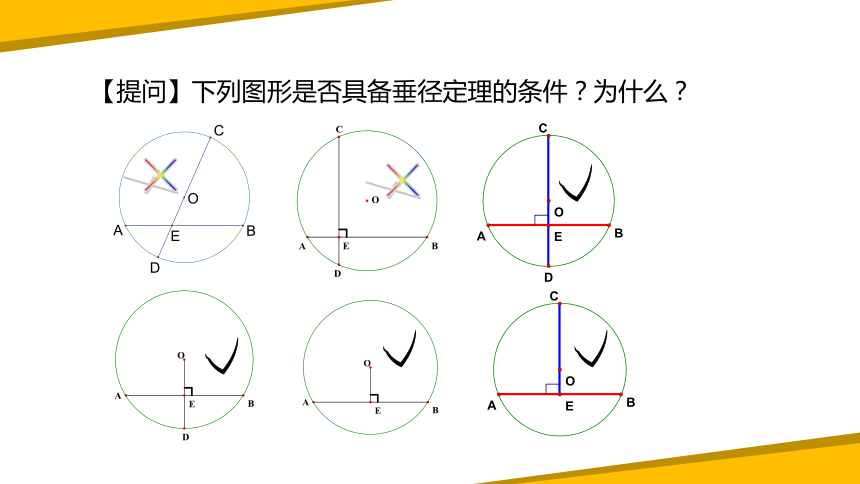
【提问】下列图形是否具备垂径定理的条件?为什么?
×
√
×
√
√
√
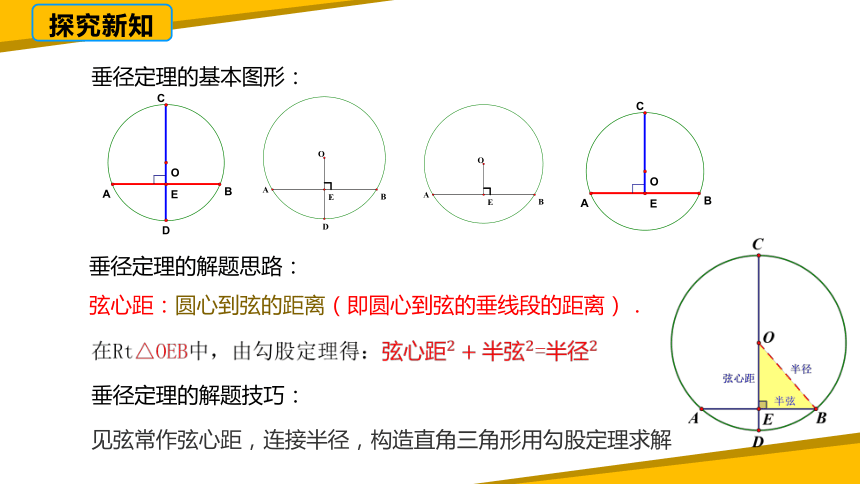
垂径定理的基本图形:
垂径定理的解题思路:
弦心距:圆心到弦的距离(即圆心到弦的垂线段的距离).
垂径定理的解题技巧:
见弦常作弦心距,连接半径,构造直角三角形用勾股定理求解
探究新知
例1 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离(弦心距)为3cm,求⊙O的半径.
A
B
.
O
E
4
3
典例解析
例2 1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37 m,拱高为7.23m,求桥拱的半径(精确到0.1m).
37
18.5
r
r-7.23
典例解析
例2 1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37 m,拱高为7.23m,求桥拱的半径(精确到0.1m).
37
18.5
r
r-7.23
典例解析
例3 下列说法正确的是( )
①平分弧的直径垂直平分弧所对的弦
②平分弦的直径平分弦所对的弧
③垂直于弦的直线必过圆心
④垂直于弦的直径平分弦所对的弧
A.②③ B.①③ C.②④ D.①④
D
典例解析
1 如图是一个圆弧形门拱,拱高1m ,跨度4m ,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
【详解】
设这个门拱的半径为r,则OB=r 1,
∵CD=4m,AB⊥CD,
∴BC= CD=2m,
在Rt△BOC中,
∵BC2+OB2=OC2 ,即22 +(r 1) 2 =r2,解得r=2.5 .
故选B.
随堂练习
2.如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面AB宽
为( )
A.4m B.5m C.6m D.8m
随堂练习
3.
随堂练习
4.
随堂练习
中考链接
B
中考链接
2.(2023.山东)下列命题正确的是( )
A.在一个三角形中至少有两个锐角
B.在圆中,垂直于弦的直径平分弦
C.如果两个角互余,那么它们的补角也互余
D.两条直线被第三条直线所截,同位角一定相等
AB
中考链接
16
课堂小结
1.垂径定理的内容?
2.垂径定理推论的内容?
当堂测试
D
当堂测试
A
当堂测试
C
当堂测试
A
当堂测试
当堂测试
8或2
当堂测试
当堂测试
分层作业
【基础达标作业】
B
分层作业
B
分层作业
A
分层作业
A
分层作业
【能力提升作业】
4
分层作业
4
分层作业
2
分层作业
【拓展延伸作业】
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
24.1.2垂直于弦的直径
学习目标
1.理解垂径定理推论;
2.能运用垂径定理及其推论解决有关问题.
复习提问
【提问】简述轴对称图形的概念?说出常见的轴对称图形?
【活动一】将你手中的圆形纸片沿着它的任意一条直径对折,重复做几次,你发现了什么?由此你能得到圆的什么特性?
圆的轴对称性:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
探究新知
【活动二】在圆形纸片上作 O的任意一条弦AB, 再作直径CD⊥AB, 垂足为E.沿着直径CD对折,你发现了什么?有哪些相等的线段和弧?
探究新知
【证明一】已知:如图,CD是⊙O的任一条直径,A是⊙O上点C,D以外任意一点,过点A作CD⊥AB,交⊙O于点B,垂足为E.求证:AE=BE.
证明:连接OA、OB,
在△OAB中,
∵OA=OB ∴△OAB是等腰三角形
又∵ CD⊥AB,
∴AE=BE
即CD是AB的垂直平分线.
这就是说对于圆上任意一点A,在圆上都有关于直线CD的对称点B,因此⊙O关于直线CD对称.
探究新知
【提问】由此你觉得垂直于弦的直径有什么特点呢?
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
垂径定理:
符号语言:
∵CD是直径,CD⊥AB
【提问】下列图形是否具备垂径定理的条件?为什么?
×
√
×
√
√
√
垂径定理的基本图形:
垂径定理的解题思路:
弦心距:圆心到弦的距离(即圆心到弦的垂线段的距离).
垂径定理的解题技巧:
见弦常作弦心距,连接半径,构造直角三角形用勾股定理求解
探究新知
例1 如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离(弦心距)为3cm,求⊙O的半径.
A
B
.
O
E
4
3
典例解析
例2 1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37 m,拱高为7.23m,求桥拱的半径(精确到0.1m).
37
18.5
r
r-7.23
典例解析
例2 1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37 m,拱高为7.23m,求桥拱的半径(精确到0.1m).
37
18.5
r
r-7.23
典例解析
例3 下列说法正确的是( )
①平分弧的直径垂直平分弧所对的弦
②平分弦的直径平分弦所对的弧
③垂直于弦的直线必过圆心
④垂直于弦的直径平分弦所对的弧
A.②③ B.①③ C.②④ D.①④
D
典例解析
1 如图是一个圆弧形门拱,拱高1m ,跨度4m ,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
【详解】
设这个门拱的半径为r,则OB=r 1,
∵CD=4m,AB⊥CD,
∴BC= CD=2m,
在Rt△BOC中,
∵BC2+OB2=OC2 ,即22 +(r 1) 2 =r2,解得r=2.5 .
故选B.
随堂练习
2.如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面AB宽
为( )
A.4m B.5m C.6m D.8m
随堂练习
3.
随堂练习
4.
随堂练习
中考链接
B
中考链接
2.(2023.山东)下列命题正确的是( )
A.在一个三角形中至少有两个锐角
B.在圆中,垂直于弦的直径平分弦
C.如果两个角互余,那么它们的补角也互余
D.两条直线被第三条直线所截,同位角一定相等
AB
中考链接
16
课堂小结
1.垂径定理的内容?
2.垂径定理推论的内容?
当堂测试
D
当堂测试
A
当堂测试
C
当堂测试
A
当堂测试
当堂测试
8或2
当堂测试
当堂测试
分层作业
【基础达标作业】
B
分层作业
B
分层作业
A
分层作业
A
分层作业
【能力提升作业】
4
分层作业
4
分层作业
2
分层作业
【拓展延伸作业】
分层作业
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
