24.1.3弧、弦、圆心角 课件(18张PPT)
文档属性
| 名称 | 24.1.3弧、弦、圆心角 课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1005.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 09:57:01 | ||
图片预览


文档简介
(共18张PPT)
人教版数学九年级上册
第24.1.3 弧、弦、圆心角
学习目标
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
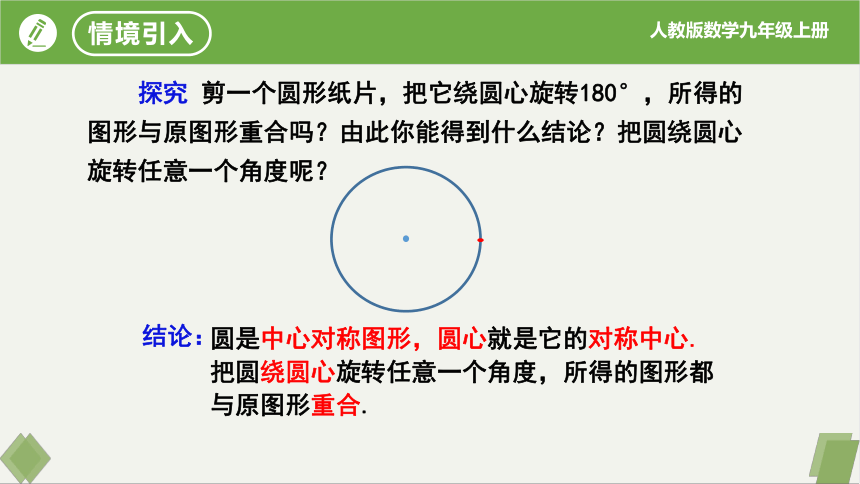
探究 剪一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?由此你能得到什么结论?把圆绕圆心旋转任意一个角度呢?
圆是中心对称图形,圆心就是它的对称中心.
把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合.
情境引入
结论:
互动新授
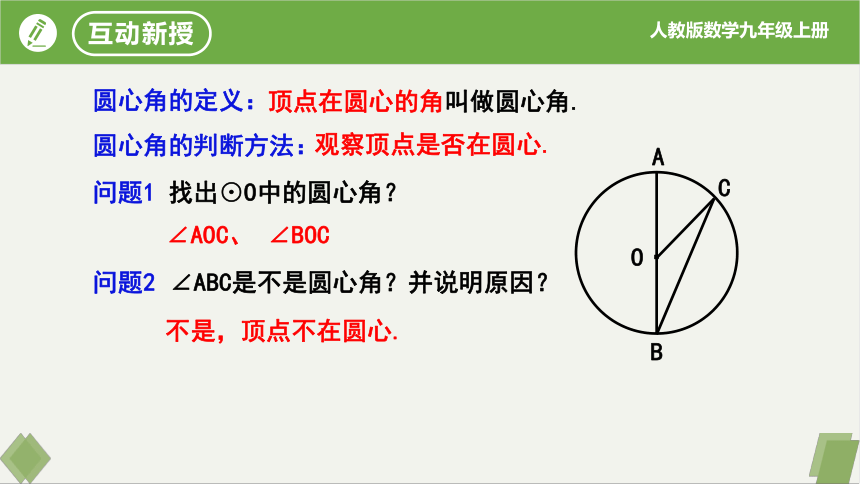
圆心角的定义:
圆心角的判断方法:
A
O·
B
C
问题1 找出⊙O中的圆心角?
问题2 ∠ABC是不是圆心角?并说明原因?
∠AOC、 ∠BOC
不是,顶点不在圆心.
顶点在圆心的角叫做圆心角.
观察顶点是否在圆心.
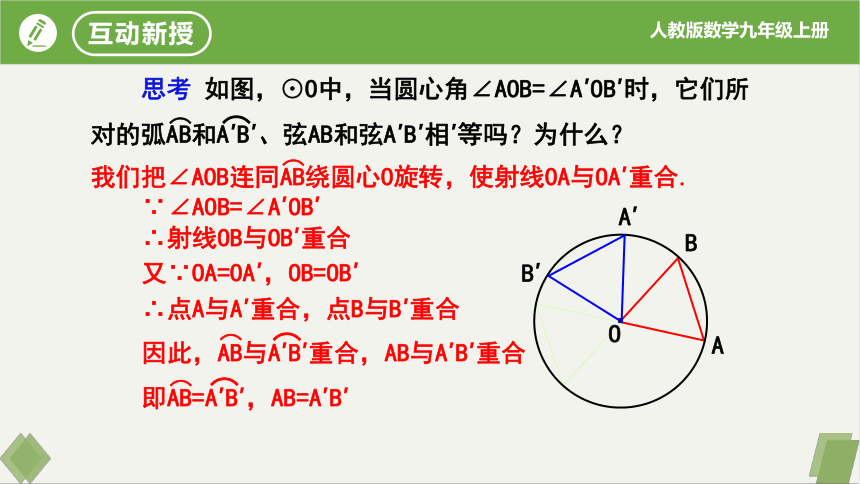
思考 如图,⊙O中,当圆心角∠AOB=∠A′OB′时,它们所对的弧AB和A′B′、弦AB和弦A′B′相′等吗?为什么?
(
(
互动新授
我们把∠AOB连同AB绕圆心O旋转,使射线OA与OA′重合.
(
·
O
A
B
A′
B′
∵∠AOB=∠A′OB′
∴射线OB与OB′重合
又∵OA=OA′,OB=OB′
∴点A与A′重合,点B与B′重合
因此,AB与A′B′重合,AB与A′B′重合
即AB=A′B′,AB=A′B′
(
(
(
(
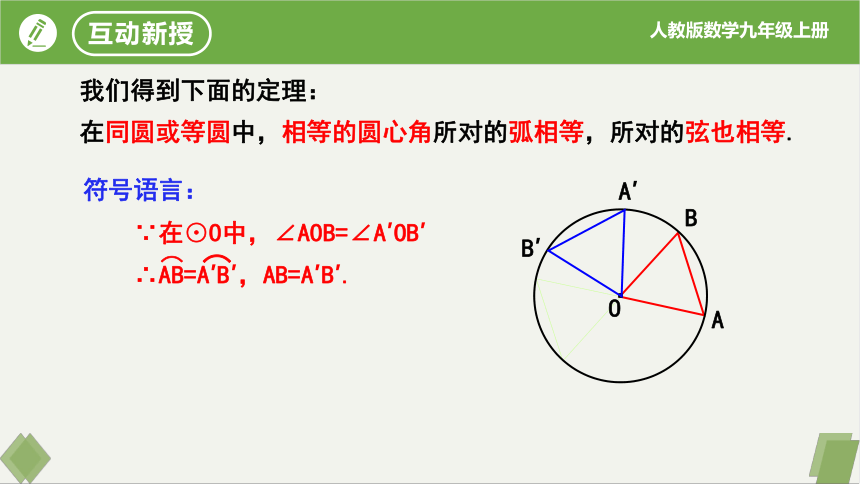
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
我们得到下面的定理:
互动新授
符号语言:
∵在⊙O中,∠AOB=∠A′OB′
∴AB=A′B′,AB=A′B′.
·
O
A
B
A′
B′
(
(
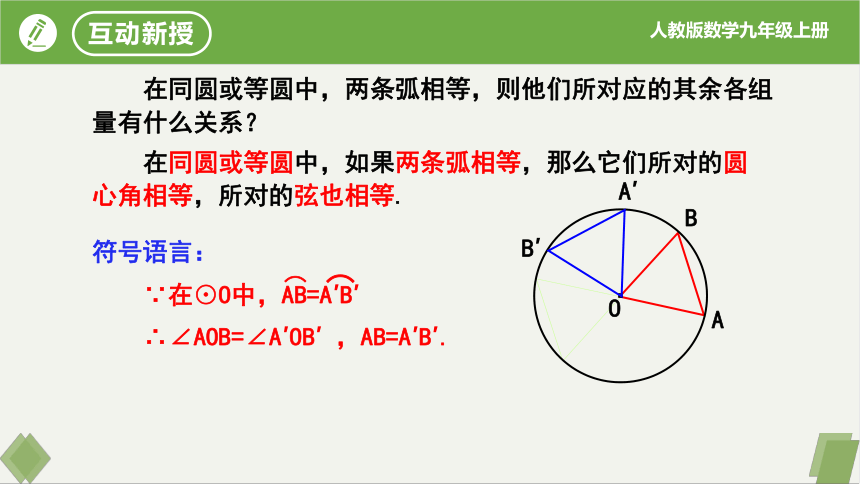
在同圆或等圆中,两条弧相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
A′
B′
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
符号语言:
∵在⊙O中,AB=A′B′
∴∠AOB=∠A′OB′ ,AB=A′B′.
(
(
互动新授
符号语言:
∵在⊙O中,AB=A′B′
∴∠AOB=∠A′OB′,AB=A′B′.
(
(
·
O
A
B
A′
B′
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,两条弦相等,则他们所对应的其余各组量有什么关系?
互动新授
·
B
C
O
A
例3 如图,在⊙O中,AB=AC,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
证明:∵AB=AC,
∴AB=AC,△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形 , AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
(
(
(
(
典例精析
1.判断下列各图中的角是不是圆心角,并说明理由.
(1) (2) (3) (4)
解:(4)是圆心角,
(1)(2)(3)不是圆心角,因为顶点不在圆心上.
小试牛刀
2.AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 _______,_____________.
(2)如果 AB=CD,那么 ________,___________.
(3)如果∠AOB=∠COD,那么 ______,_______ .
(
(
小试牛刀
·
C
A
B
D
E
F
O
AB=CD
AB=CD
∠AOB=∠COD
∠AOB=∠COD
AB=CD
(
(
AB=CD
(
(
1.如图,AB是⊙O的直径,BC=CD=DE,∠AOE=66°,则∠COD的度数是( )
A.108° B.72° C.48° D.38°
2.如图,已知AB是⊙O的直径,C、D是半圆上两个三等分点,则∠COD= .
3.如图,在⊙O中,点C是AB的中点,∠A=70°,则∠BOC= .
60°
20°
D
课堂检测
4.已知:如图,在⊙O中,弦AB和CD相交,连接AC、BD,且AC=BD.求证:AB=CD.
课堂检测
1.如图,AB是⊙O的直径, ∠COD=35°,求∠AOE的度数.
·
A
O
B
C
D
E
解:
∵
拓展训练
课堂小结
圆心角的定义:
顶点在圆心的角叫做圆心角.
得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的、弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
A
C
课后作业
3.弦长等于半径的弦所对的圆心角等于_______.
4.若一条弦把圆分成1:3两部分,则劣弧所对的圆心角的度数为______.
5.如图,AB是☉O的直径,AC,CD,DE,EF,FB都是☉O的弦,且AC=CD=DE=EF=FB,则∠AOC=______,∠COF=______.
60°
90°
36°
108°
课后作业
谢谢聆听
人教版数学九年级上册
第24.1.3 弧、弦、圆心角
学习目标
1.理解圆心角的概念,掌握圆的中心对称性和旋转不变性.
2.探索圆心角、弧、弦之间关系定理并利用其解决相关问题.
3.理解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
探究 剪一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?由此你能得到什么结论?把圆绕圆心旋转任意一个角度呢?
圆是中心对称图形,圆心就是它的对称中心.
把圆绕圆心旋转任意一个角度,所得的图形都与原图形重合.
情境引入
结论:
互动新授
圆心角的定义:
圆心角的判断方法:
A
O·
B
C
问题1 找出⊙O中的圆心角?
问题2 ∠ABC是不是圆心角?并说明原因?
∠AOC、 ∠BOC
不是,顶点不在圆心.
顶点在圆心的角叫做圆心角.
观察顶点是否在圆心.
思考 如图,⊙O中,当圆心角∠AOB=∠A′OB′时,它们所对的弧AB和A′B′、弦AB和弦A′B′相′等吗?为什么?
(
(
互动新授
我们把∠AOB连同AB绕圆心O旋转,使射线OA与OA′重合.
(
·
O
A
B
A′
B′
∵∠AOB=∠A′OB′
∴射线OB与OB′重合
又∵OA=OA′,OB=OB′
∴点A与A′重合,点B与B′重合
因此,AB与A′B′重合,AB与A′B′重合
即AB=A′B′,AB=A′B′
(
(
(
(
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
我们得到下面的定理:
互动新授
符号语言:
∵在⊙O中,∠AOB=∠A′OB′
∴AB=A′B′,AB=A′B′.
·
O
A
B
A′
B′
(
(
在同圆或等圆中,两条弧相等,则他们所对应的其余各组量有什么关系?
·
O
A
B
A′
B′
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
符号语言:
∵在⊙O中,AB=A′B′
∴∠AOB=∠A′OB′ ,AB=A′B′.
(
(
互动新授
符号语言:
∵在⊙O中,AB=A′B′
∴∠AOB=∠A′OB′,AB=A′B′.
(
(
·
O
A
B
A′
B′
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,两条弦相等,则他们所对应的其余各组量有什么关系?
互动新授
·
B
C
O
A
例3 如图,在⊙O中,AB=AC,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
证明:∵AB=AC,
∴AB=AC,△ABC是等腰三角形.
∵∠ACB=60°,
∴△ABC是等边三角形 , AB=BC=CA.
∴∠AOB=∠BOC=∠AOC.
(
(
(
(
典例精析
1.判断下列各图中的角是不是圆心角,并说明理由.
(1) (2) (3) (4)
解:(4)是圆心角,
(1)(2)(3)不是圆心角,因为顶点不在圆心上.
小试牛刀
2.AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么 _______,_____________.
(2)如果 AB=CD,那么 ________,___________.
(3)如果∠AOB=∠COD,那么 ______,_______ .
(
(
小试牛刀
·
C
A
B
D
E
F
O
AB=CD
AB=CD
∠AOB=∠COD
∠AOB=∠COD
AB=CD
(
(
AB=CD
(
(
1.如图,AB是⊙O的直径,BC=CD=DE,∠AOE=66°,则∠COD的度数是( )
A.108° B.72° C.48° D.38°
2.如图,已知AB是⊙O的直径,C、D是半圆上两个三等分点,则∠COD= .
3.如图,在⊙O中,点C是AB的中点,∠A=70°,则∠BOC= .
60°
20°
D
课堂检测
4.已知:如图,在⊙O中,弦AB和CD相交,连接AC、BD,且AC=BD.求证:AB=CD.
课堂检测
1.如图,AB是⊙O的直径, ∠COD=35°,求∠AOE的度数.
·
A
O
B
C
D
E
解:
∵
拓展训练
课堂小结
圆心角的定义:
顶点在圆心的角叫做圆心角.
得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的、弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.
A
C
课后作业
3.弦长等于半径的弦所对的圆心角等于_______.
4.若一条弦把圆分成1:3两部分,则劣弧所对的圆心角的度数为______.
5.如图,AB是☉O的直径,AC,CD,DE,EF,FB都是☉O的弦,且AC=CD=DE=EF=FB,则∠AOC=______,∠COF=______.
60°
90°
36°
108°
课后作业
谢谢聆听
同课章节目录
