24.1.3弧、弦、圆心角 课件(38张PPT)
文档属性
| 名称 | 24.1.3弧、弦、圆心角 课件(38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览






文档简介
(共38张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
24.1.3弧、弦、圆周角
学习目标
1.理解圆心角的概念和圆的旋转不变性,会辨析圆心角.
2.掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的证明和计算.
3.在探索弧、弦、圆心角的关系的过程中,学会运用转化的数学思想解决问题.
复习提问
【提问】简述中心对称图形的概念?说出常见的中心对称图形?
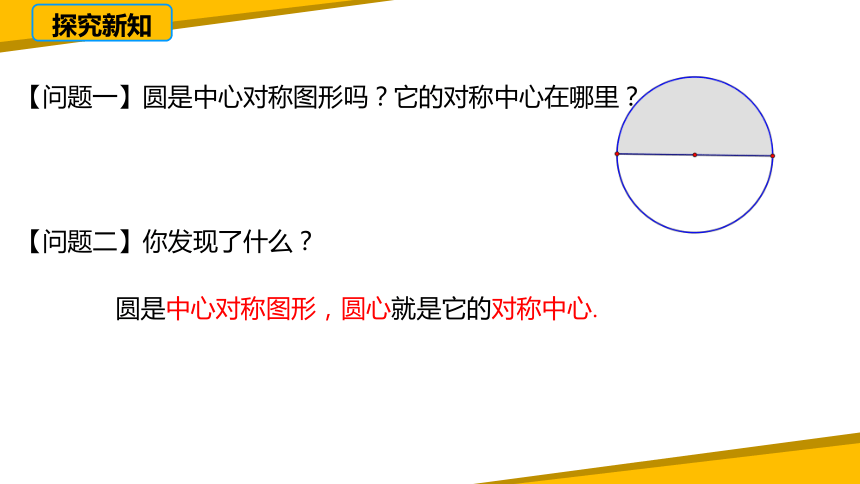
【问题一】圆是中心对称图形吗?它的对称中心在哪里?
【问题二】你发现了什么?
圆是中心对称图形,圆心就是它的对称中心.
探究新知
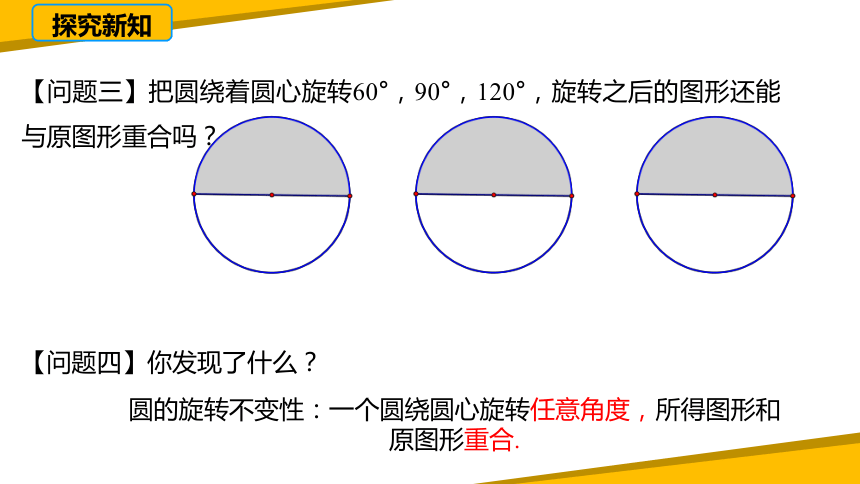
【问题三】把圆绕着圆心旋转60°,90°,120°,旋转之后的图形还能与原图形重合吗?
【问题四】你发现了什么?
圆的旋转不变性:一个圆绕圆心旋转任意角度,所得图形和原图形重合.
探究新知
【提问】观察下图,它们有什么共同点?
顶点是圆心
圆心角的定义:
圆心角的判断方法:
顶点在圆心的角叫做圆心角.
观察顶点是否在圆心.
探究新知
【问题】任意圆心角,对应会出现哪几个量?
【猜想】你觉得这几个量会有什么关系呢?
圆心角、弧、弦
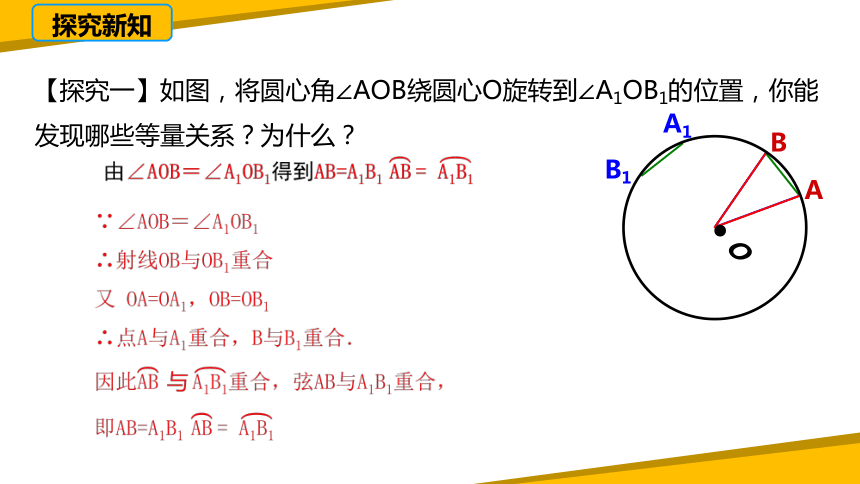
【探究一】如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
B
A
A1
B1
● O
探究新知
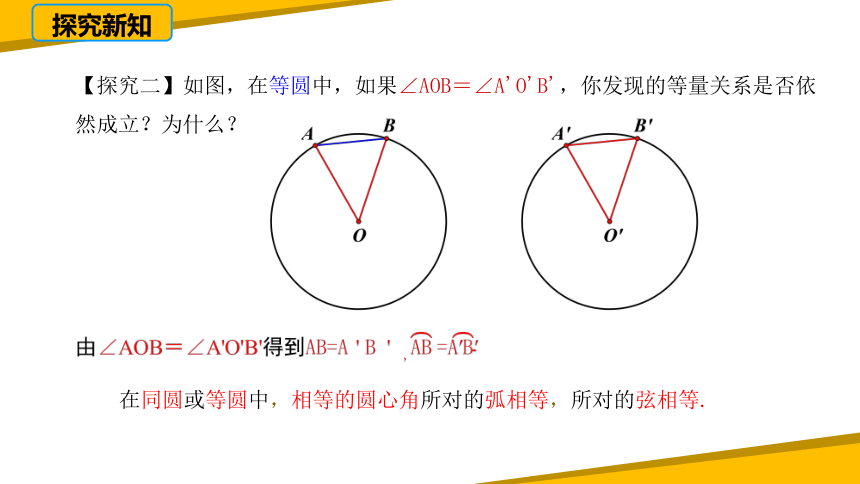
【探究二】如图,在等圆中,如果∠AOB=∠A'O'B',你发现的等量关系是否依然成立?为什么?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
探究新知
【提问】定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
探究新知
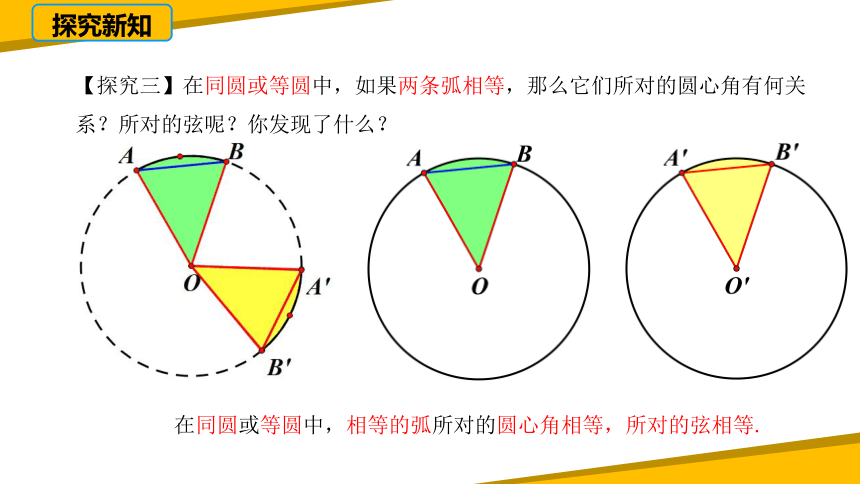
【探究三】在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角有何关系?所对的弦呢?你发现了什么?
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
探究新知
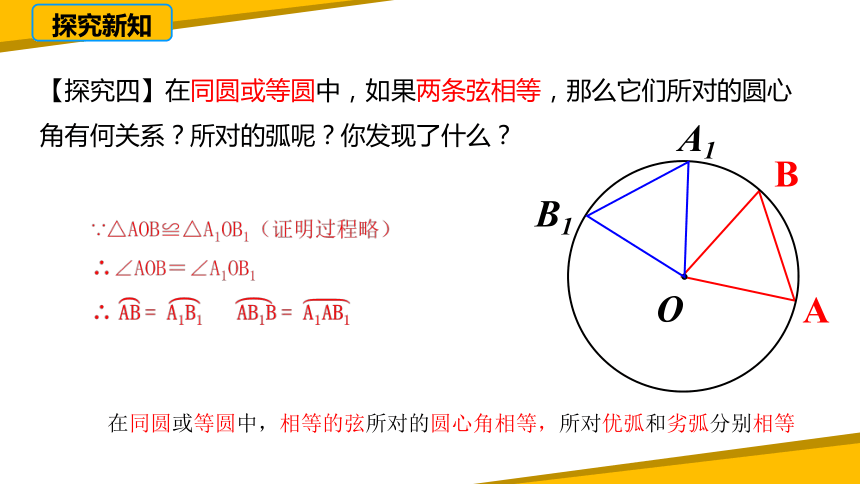
【探究四】在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角有何关系?所对的弧呢?你发现了什么?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等
探究新知
【提问】简述同圆和等圆中,圆心角、弧、弦之间的关系吗?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等.
【总结】在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
建立模型
例1 回答下面问题:
1.找出⊙O中的圆心角?
2.∠ABC是不是圆心角?并说明原因?
A
O·
B
C
∠AOC、 ∠BOC
不是,顶点不在圆心.
典例解析
·
C
A
B
D
E
F
O
AB=CD
AB=CD
∵AB=CD,∴∠AOB=∠COD.
∵AO=CO,BO=DO,则△AOB ≌ △COD.
而OE、OF是AB与CD对应边上的高,
∴OE=OF.
典例解析
60°
20°
随堂练习
随堂练习
随堂练习
中考链接
A
中考链接
课堂小结
1.圆具有怎样的对称性?
2.圆心角的概念?
3.在同圆与等圆中,圆心角、弧、弦之间有何关系?
当堂测试
B
当堂测试
C
当堂测试
C
当堂测试
B
当堂测试
当堂测试
50
当堂测试
当堂测试
分层作业
B
分层作业
B
分层作业
D
分层作业
D
分层作业
分层作业
分层作业
24
分层作业
【拓展延伸作业】
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
24.1.3弧、弦、圆周角
学习目标
1.理解圆心角的概念和圆的旋转不变性,会辨析圆心角.
2.掌握在同圆或等圆中,圆心角与其所对的弦、弧之间的关系,并能运用此关系进行相关的证明和计算.
3.在探索弧、弦、圆心角的关系的过程中,学会运用转化的数学思想解决问题.
复习提问
【提问】简述中心对称图形的概念?说出常见的中心对称图形?
【问题一】圆是中心对称图形吗?它的对称中心在哪里?
【问题二】你发现了什么?
圆是中心对称图形,圆心就是它的对称中心.
探究新知
【问题三】把圆绕着圆心旋转60°,90°,120°,旋转之后的图形还能与原图形重合吗?
【问题四】你发现了什么?
圆的旋转不变性:一个圆绕圆心旋转任意角度,所得图形和原图形重合.
探究新知
【提问】观察下图,它们有什么共同点?
顶点是圆心
圆心角的定义:
圆心角的判断方法:
顶点在圆心的角叫做圆心角.
观察顶点是否在圆心.
探究新知
【问题】任意圆心角,对应会出现哪几个量?
【猜想】你觉得这几个量会有什么关系呢?
圆心角、弧、弦
【探究一】如图,将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置,你能发现哪些等量关系?为什么?
B
A
A1
B1
● O
探究新知
【探究二】如图,在等圆中,如果∠AOB=∠A'O'B',你发现的等量关系是否依然成立?为什么?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
探究新知
【提问】定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
探究新知
【探究三】在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角有何关系?所对的弦呢?你发现了什么?
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
探究新知
【探究四】在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角有何关系?所对的弧呢?你发现了什么?
·
O
A
B
B1
A1
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等
探究新知
【提问】简述同圆和等圆中,圆心角、弧、弦之间的关系吗?
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,相等的弧所对的圆心角相等,所对的弦相等.
在同圆或等圆中,相等的弦所对的圆心角相等,所对优弧和劣弧分别相等.
【总结】在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
建立模型
例1 回答下面问题:
1.找出⊙O中的圆心角?
2.∠ABC是不是圆心角?并说明原因?
A
O·
B
C
∠AOC、 ∠BOC
不是,顶点不在圆心.
典例解析
·
C
A
B
D
E
F
O
AB=CD
AB=CD
∵AB=CD,∴∠AOB=∠COD.
∵AO=CO,BO=DO,则△AOB ≌ △COD.
而OE、OF是AB与CD对应边上的高,
∴OE=OF.
典例解析
60°
20°
随堂练习
随堂练习
随堂练习
中考链接
A
中考链接
课堂小结
1.圆具有怎样的对称性?
2.圆心角的概念?
3.在同圆与等圆中,圆心角、弧、弦之间有何关系?
当堂测试
B
当堂测试
C
当堂测试
C
当堂测试
B
当堂测试
当堂测试
50
当堂测试
当堂测试
分层作业
B
分层作业
B
分层作业
D
分层作业
D
分层作业
分层作业
分层作业
24
分层作业
【拓展延伸作业】
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华
同课章节目录
