24.1.1圆 课件（49张PPT）

(共49张PPT)
新课标 人教版 九年级上册
2023-2024学年度上学期人教版精品课件
第二十四章圆
24.1.1圆
1.理解圆的定义及表示方法.
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆有关的概念，并了解它们之间的区别和联系.
学习目标
情境引入
观察下列生活中的图片，找一找你所熟悉的图形.
圆是常见的图形，生活中的许多物体都给我们以圆的形象
探究新知
我们在小学已经对圆有了初步认识，如图，观察画圆的过程，你能说出圆是如何画出来的吗？
探究新知
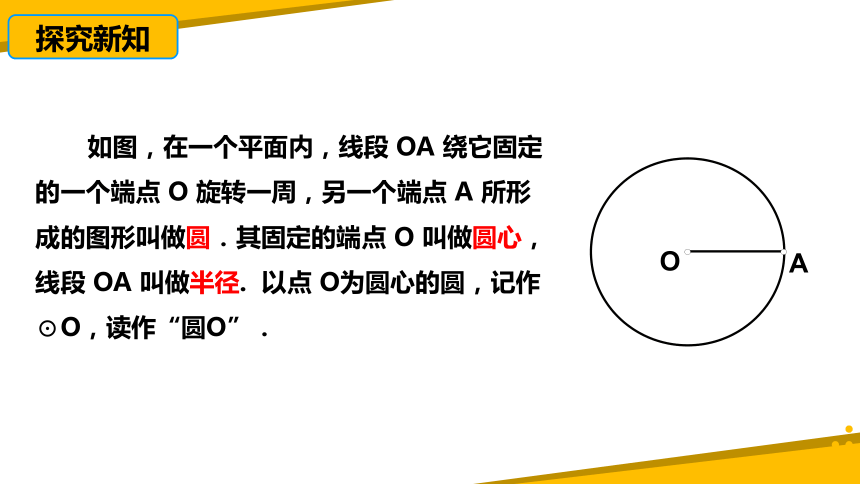
如图，在一个平面内，线段 OA 绕它固定的一个端点 O 旋转一周，另一个端点 A 所形成的图形叫做圆．其固定的端点 O 叫做圆心，线段 OA 叫做半径. 以点 O为圆心的圆，记作⊙O，读作“圆O”．
概念精析
1.确定一个圆需要“两个要素”，一是圆心：圆心定其位置;
二是半径：半径定其大小.
2.圆是一条封闭的曲线，曲线是“圆周”，而不能认为是“圆面”.
3.“圆上的点”指圆周上的点.
合作探究
尝试画出一个圆，在画圆的过程中你发现了什么？
方法一
方法二
方法三
·
利用图钉画圆
探究新知
(1) 圆上各点到定点（圆心O）的距离都等于 ．
(2) 到定点的距离等于定长的点都在 ．
在画圆的过程中我发现：
结论：
圆心为O，半径为 r 的圆可以看成是所有到定点O的距离等于定长 r 的点的集合.
定长 r
同一个圆上
探究新知
C
A
·
O
B
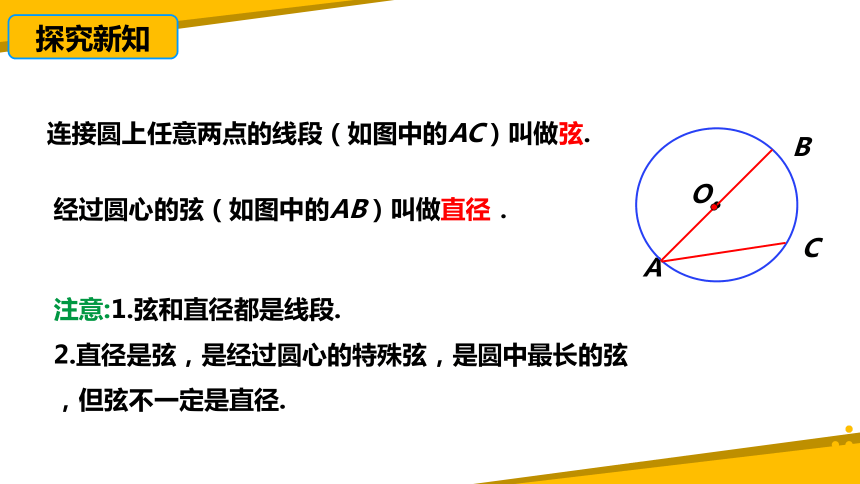
连接圆上任意两点的线段（如图中的AC）叫做弦.
经过圆心的弦（如图中的AB）叫做直径．
注意:1.弦和直径都是线段.
2.直径是弦，是经过圆心的特殊弦，是圆中最长的弦，但弦不一定是直径.
探究新知
半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．
劣弧与优弧：小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
·
C
O
A
B
·
C
O
A
B
探究新知
等圆: 能够重合的两个圆叫做等圆.
·
C
O1
A
容易看出：等圆是两个半径相等的圆.
等弧:在同圆或等圆中，能够互相重合的弧叫做等弧.
·
C
O
A
概念精练
1.下列语句中：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，弧不一定是半圆. 正确的有_________ .
解析：直径是最长的弦，故①正确；直径是过圆心的弦，但弦不一定是直径，故②错误；半径相等的两个半圆能互相重合，所以是等弧，故③正确；在同圆或等圆中，长度相等的两条弧才是等弧，故④错误；弧分为劣弧、优弧、半圆，故⑤正确.
①③⑤
概念精练
2.如图，如果弧AB和弧CD的拉直长度都是10 cm，平移并调整小圆的位置，是否能使这两条弧完全重合？
这两条弧不可能完全重合，因为这两条弧弯曲程度不同，“等弧”不等于“长度相等的弧”，等弧仅仅存在于同圆或者等圆中.
例题讲解
例 矩形ABCD 的对角线AC,BD相交于点O.求证：A,B,C,D 四个点在以点O为圆心的同一个圆上.
A
B
C
D
O
证明：∵四边形ABCD为矩形，
∴OA=OC= AC,OB=OD= BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心，OA为半径的圆上.
随堂练习
1.判断下列说法的正误：
(1)弦是直径；( )
(2)半圆是弧； ( )
(3)过圆心的线段是直径； ( )
(7)圆心相同，半径相等的两个圆是同心圆;( )
(8)半径相等的两个圆是等圆.( )
(4)过圆心的直线是直径；( )
(5)半圆是最长的弧；( )
(6)直径是最长的弦；( )
随堂练习
2.下列关于圆的叙述正确的是(　　)
A．圆是由圆心唯一确定的
B．圆是一条封闭的曲线
C．到定点的距离小于或等于定长的所有点组成圆
D．圆内任意一点到圆心的距离都相等
B
随堂练习
3.以下命题：(1)半圆是弧，但弧不一定是半圆；(2)过圆上任意一点只能作一条弦，且这条弦是直径；(3)弦是直径；(4)直径是圆中最长的弦；(5)直径不是弦；(6)优弧大于劣弧；(7)以O为圆心可以画无数个圆. 正确的个数为(　 　)
A．1　 　 B．2　 　 C．3　　 　D．4
C
随堂练习
4.下列说法中, 错误的有( )
(1)经过点P 的圆有无数个； (2)以点P 为圆心的圆有无数个；
(3)半径为3 cm 且经过点P 的圆有无数个；
(4)以点P 为圆心，3 cm 长为半径的圆有无数个.
A. 1 个 B. 2 个 C. 3 个 D. 4 个
A
随堂练习
5.如图所示，在⊙O中，点A，O，D以及点
B，O，C分别在一条直线上，则图中的弦有( )
A．2条 B．3条 C．4条 D．5条
B
6.半径为5的圆的一条弦长不可能是(　 )
A．3 B．5 C．10 D．12
D
随堂练习
7.如何在操场上画一个半径是5m的圆？说出你的理由.
首先确定圆心, 然后用5米长的绳子一端固定为圆心端,另一端系在一端尖木棒,木棒以5米长尖端划动一周,所形成的图形就是所画的圆.
随堂练习
8.已知：如图，在△ABC中，∠C=90°，求证：A、B、C三点在同一个圆上.
证明：作AB的中点O，连接OC.
∵△ABC是直角三角形.
∴OA=OB=OC= AB.
∴A、B、C三点在同一个圆上.
B
A
C
中考链接
1．(2023年 苏家屯区 一模试卷)下列叙述中不正确的是（　　）
A．圆是中心对称图形，圆心是它的对称中心
B．圆是轴对称图形，直径是它的对称轴
C．连接圆上两点的线段叫弦
D．圆上两点间的部分叫弧
B
中考链接
2.（2023年 四十六教育集团 二模试卷）如图，在 中，点B、O、C和点A、O、D分别在同一条直线上，则图中有（　　）条弦．
A.2 B.3 C.4 D.5
B
中考链接
3.（2023年 六十九中学 一模试卷）如图，半径为1的圆从表示1的点开始沿着数轴向左滚动一周，圆上的点A与表示1的点重合，滚动一周后到达点B，点B表示的数是（　　）
A．﹣2π B．1﹣2π C．﹣π D．1﹣π
B
中考链接
4.（2023年 一八四中学 一模试卷）已知：如图，在⊙O中，AB为弦，C、D两点在 AB上，且AC=BD．求证：OC=OD．
证明：∵OA、OB为⊙O的半径，
∴OA=OB. ∴∠A=∠B.
又∵AC=BD，
∴△ACO≌△BDO.
∴OC=OD.
课堂小结
圆的基本概念
圆的定义
与圆有关的概念
形成性定义：
集合性定义：
弦：
直径：
圆弧（弧）：
半圆：
等圆、等弧：
优弧、劣弧：
在一个平面内，线段OA绕它固定的一个端点O旋
转一周，另一个端点A所形成的图形叫做圆.
圆心为O、半径为r的圆可以看成是所有到定点O
的距离等定长r的点的.
连接圆上任意两点的线段叫做弦.
直径是经过圆心的弦，是圆中最长的弦.
圆的任意一条直径的两个端点把圆分成两条弧，每条弧
都叫做半圆.
能够重合的两个圆叫做等圆，在同圆或等圆中，
能够互相重合的弧叫做等弧.
大于半圆的弧叫做优弧，小于半圆的弧叫做劣弧.
圆上任意两点间的部分叫做圆弧，简称弧.
1.下列说法正确的是( )
A.四边形的四个顶点都在同一个圆上
B.菱形的四个顶点都在同一个圆上
C.矩形的四个顶点都在同一个圆上
D.平行四边形的四个顶点都在同一个圆上
C
当堂测试
当堂测试
2. 下列说法错误的是（　 　）
A．直径是圆中最长的弦 B．长度相等的两条弧是等弧
C．面积相等的两个圆是等圆 D．半径相等的两个半圆是等弧
B
当堂测试
3．如图，点A，B，C在⊙O上，点O在线段AC上，点
D在线段AB上，下列说法正确的是(　　)
A．线段AB，AC，CD，OB都是弦
B．与线段OB相等的线段有OA，OC，CD
C．图中的优弧有2条
D．AC是弦，AC又是⊙O的直径，所以弦是直径
C
4.下列说法中正确的是（ ）
①直径相等的两个圆是等圆　　②长度相等的两条弧是等弧
③圆中最长的弦是通过圆心的弦　
④一条弦把圆分成两条弧，这两条弧不可能是等弧
Ａ．①③ 　　　Ｂ．②③④
Ｃ．①④　 　　 D．①
当堂测试
A
分层作业
【能力提升作业】
5.下列说法：
①优弧一定比劣弧长；②面积相等的两个圆是等圆；③长度相等的弧是等弧；④经过圆内的一个定点可以作无数条弦；⑤经过圆内一定点可以作无数条直径．其中不正确的个数是（　　）
A.1个 B.2个 C.3个 D.4个
C
6.一点和⊙O上的最近点距离为4cm,最远的距离为10cm,则这个圆的半径是 .
7cm或3cm
当堂测试
当堂测试
7.如图，菱形ABCD的对角线AC和BD相交于点O.E，F，G，H 分别为边AB，BC，CD，DA 的中点，那么点E，F，G，H 是否在同一个圆上？请说明理由.
当堂测试
同理可得，OF= BC，OG= CD，OH= DA.
∴ OE=OF=OG=OH.
∴点E，F，G，H 在以点O 为圆心，OE 为半径的圆上.
分层作业
【基础达标作业】
1．下列条件中，能确定一个圆的是（　　）
A．以点O为圆心
B．以10m长为半径
C．以点A为圆心，4cm长为半径
D．经过已知点M
C
2．下列说法：①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，但弧不一定是半圆．正确的说法有（　　）
A．1个 B．2个 C．3个 D．4个
C
分层作业
【基础达标作业】
3．如图所示，MN为⊙O的弦，∠N＝52°，则∠MON的度数为（　　）
A．38° B．52° C．76° D．104°
C
分层作业
【基础达标作业】
4．已知⊙O的半径是6cm，则⊙O中最长的弦长是（　　）
A．6cm B．12cm C．16cm D．20cm
B
5．如图，图中的弦共有（　　）
A．1条 B．2条 C．3条 D．4条
B
分层作业
【基础达标作业】
6.你见过树木的年轮吗 从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径平均每年增加多少
解： 23÷2÷20=0.575(cm)
答:这棵红衫树的半径每年增加0.575cm.
分层作业
【能力提升作业】
7．由所有到已知点O的距离大于或等于2，并且小于或等于3的点组成的图形的面积为（　　）
A．4π B．9π C．5π D．13π
B
分层作业
【能力提升作业】
8.如图，AB、AC为⊙O的弦，连接CO、BO并延长分别交弦AB、AC于
点E、F，∠B＝∠C．求证：CE＝BF．
分层作业
【能力提升作业】
8.证明：∵在△BOE和△COF中，
∴△BOE≌△COF（ASA），
∴OE＝OF，
又∵OB＝OC
∴OE+OC＝OF+OB
∴CE＝BF．
分层作业
【能力提升作业】
9.已知：如图，BD、CE是△ABC的高，M为BC的中点．试说明点
B、C、D、E在以点M为圆心的同一个圆上．
分层作业
【能力提升作业】
∴点B、C、D、E在以点M为圆心的同一圆上．
分层作业
【拓展延伸作业】
10.如图，AB是⊙O的弦，点C是优弧AB上的动点（C不与A、B重合），
CH⊥AB，垂足为H，点M是BC的中点．若⊙O的半径是3，则MH长的
最大值是（　　）
A．3 B．4 C．5 D．6
A
分层作业
【拓展延伸作业】
11.如图a，直线l经过⊙O的圆心O，且与⊙O交于A，B两点，点C在⊙O
上，且∠AOC＝30°，点P是直线l上的一个动点（与圆心O不重合），直线
CP与⊙O相交于点Q．
（1）如图b，当点P在半径OA上时，若QP＝QO，求∠OCP的度数．
（2）当点P在直线l上其他位置时，是否还存在∠OCP使得QP＝QO？
若存在，请求出∠OCP的度数；若不存在，请说明理由．
分层作业
【拓展延伸作业】
解：（1）如图1，设∠QPO＝x，
∵PQ＝QO，
∴∠QOP＝∠QPO＝x，
∴∠Q＝180°﹣2x，
∵OQ＝OC，
∴∠C＝180°﹣2x，
∵∠OPQ＝∠C+∠POC，
∴180°﹣2x+30°＝x，解得x＝70°，
∴∠OCP＝180°﹣2×70°＝40°；
分层作业
【拓展延伸作业】
（2）存在，
如图2，设∠QOC＝x，则∠QOP＝x+30°，
∵QO＝QP，∴∠QPO＝∠QOP＝x+30°，
∴∠QCO＝∠COP+∠CPO＝30°+x+30°＝x+60°，
∵OQ＝OC，∴∠OQC＝∠OCQ＝x+60°，
∴x+x+60°+x+60°＝180°，解得x＝20°，
∴∠OCP＝∠QOC+∠OQC＝20°+20°+60°＝100°；
当点Q与C点重合时，；
∵QP=QO，
∴∠POC=∠CPO=30°，
∴∠OCP=180°-∠POC-∠CPO=180°-30°-30°=120°．
分层作业
【拓展延伸作业】
如图3，设∠QPO＝x，
∵PQ＝QO，
∴∠QOP＝∠QPO＝x，
∴∠CQO＝2x，
而OC＝OQ，
∴∠C＝2x，
∵∠AOC＝∠APC+∠C，
∴x+2x＝30°，解得x＝10°，
∴∠OCP＝2x＝20°．
综上所述：∠OCP的度数是100°，120°，20°．
祝所有同学
会用数学的眼光观察现实世界
会用数学的思维思考现实世界
会用数学的语言表达现实世界
不负韶华