25.1.1 随机事件 课件(26张PPT)
文档属性
| 名称 | 25.1.1 随机事件 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
第25章 概率初步
25.1.1 随机概率
第五单元
1 理解必然事件、不可能事件、随机事件的概念,能辨别随机事件;
2 会简单分析事件发生的可能性;
3 经历体验、操作、观察、归纳、总结的过程,发展学生从复杂的表象中,提炼出本质特征并加以抽象概括的能力.
情景引入
探究新知
新知讲解
探究新知
典例分析
典例分析
针对训练
探究新知
新知讲解
针对训练
能力提升
直击中考
归纳小结
归纳小结
布置作业
下图为实际生活的具体现象,你觉得这些现象是否一定会发生?
太阳东升西落
天气预报显示
明天可能下雨
太阳绕着地球转
可能发生
一定发生
不可能发生
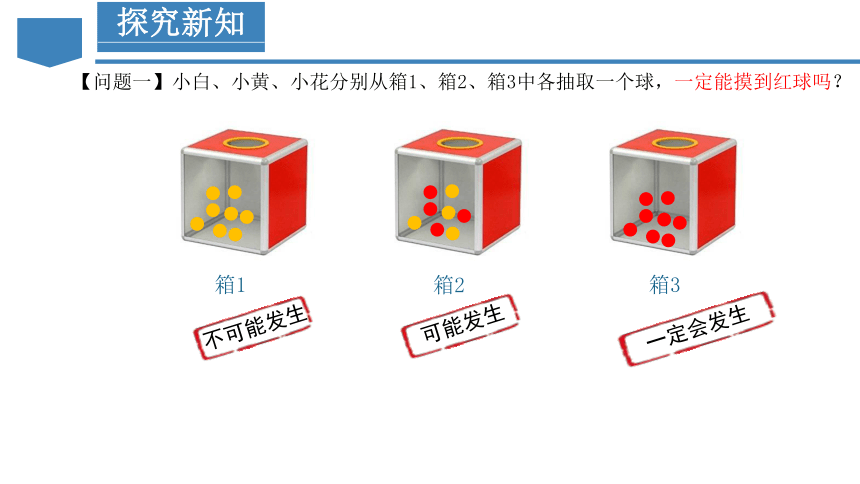
【问题一】小白、小黄、小花分别从箱1、箱2、箱3中各抽取一个球,一定能摸到红球吗?
箱1
箱3
箱2
不可能发生
可能发生
一定会发生
【问题二】 5名同学参加演讲比赛,以抽扑克牌的方式决定每个人的出场顺序.现桌面上有5张扑克牌(背面花色相同),牌面分别是1,2,3,4,5.小军首先抽签,他在看不到的扑克牌上数字的情况从桌面上随机(任意)地取一张扑克.
1)抽到的扑克牌有几种可能的结果?
2)抽到的扑克牌牌面数字会小于6吗?
3)抽到的扑克牌牌面数字会是0吗?
4)抽到的扑克牌牌面数字会是1吗?
五种可能,数字1-5都可能被抽到.
结果必然小于6.
结果不可能为0.
可能是1,也可能不是1,结果无法确定.
在一定条件下:
1)必然会发生的事件叫必然事件;
2)必然不会发生的事件叫不可能事件;
3)可能会发生,也可能不发生的事件叫不确定事件或随机事件.
【问题三】小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数.请考虑以下问题,掷一次骰子,观察骰子向上的一面:
1)可能出现哪些点数?
2) 出现的点数会是7吗?
3) 出现的点数大于0吗?
4) 出现的点数会是4吗?
5) 判断2)3)4)出现的事件属于哪种事件?
1,2,3,4,5,6
肯定不会是7.
肯定大于0.
出现点数可能是4,也可能不是4,结果无法确定.
2)为不可能事件
3)必然事件
4)随机事件
不可能事件
必然事件
确定性事件
随机事件
事件
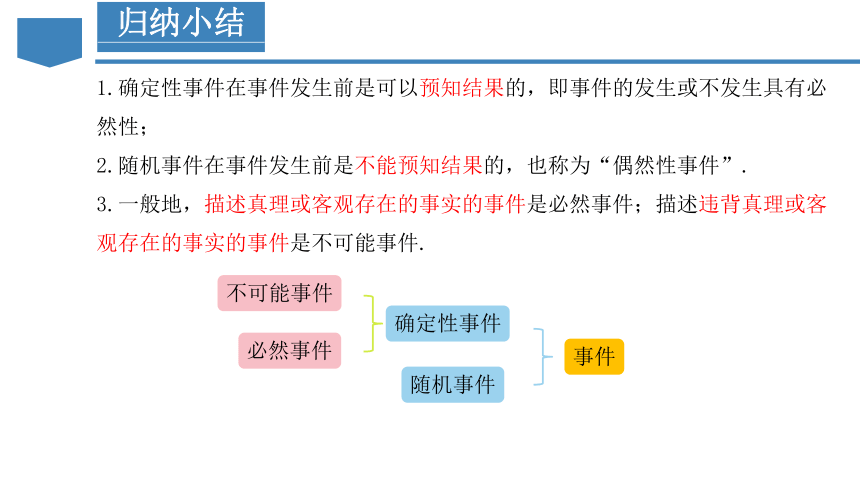
1.确定性事件在事件发生前是可以预知结果的,即事件的发生或不发生具有必然性;
2.随机事件在事件发生前是不能预知结果的,也称为“偶然性事件”.
3.一般地,描述真理或客观存在的事实的事件是必然事件;描述违背真理或客观存在的事实的事件是不可能事件.
例1 判断下列事件属于哪种事件
1.将一小勺食盐放入开水中,食盐缓慢溶解.
2.测量某天的最高气温,结果为100℃.
3.小强打开电视机,电视里正在播放电视剧.
4.互为相反数的两个数的和等于0.
5.2019年2月的天数有29天.
必然事件
不可能事件
随机事件
必然事件
不可能事件
1. 下列事件中,①打开电视,它正在播关于扬州特产的广告;②太阳绕着地球转;③掷一枚正方体骰子,点数“4”朝上;④13人中至少有2人的生日是同一个月.属于随机事件的个数是 .
2. 一盒乒乓球中共有6只,其中2只次品,4只正品,正品和次品大小和形状完全相同,每次任取3只,出现了下列事件,指出这些事件分别是什么事件.
1)3只正品.
2)至少有一只次品.
3)3只次品.
4)至少有一只正品.
2
随机事件
随机事件
不可能事件
必然事件
小组讨论:
1.两人一组,两人轮流举事件,对方判断是什么事件;
2.两位同学讨论,全班交流,深化概念.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
1)这个球是白球还是黑球?
2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗并说明原因?
可能是白球,也可能是黑球.
不一样,黑球的数量大于白球数量,则摸出黑球的可能性大于白球的可能性.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
3)你能验证你的猜想吗?由此你发现了什么?
1.每名同学随机从袋子摸出一个球,记下球的颜色,并放回摇匀;
2.汇总全班的摸球结果,填在下表中.
球的颜色 黑球 白球
摸取次数
33
17
一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
4)能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
1.白球个数不变, 拿出两个黑球;
2.黑球个数不变,加入2个白球.
【问题五】能否通过改变盒中红、黄球的数量,在摸一个球的前提下,使“摸出红球”和“摸出黄球”的可能性大小相同?(不改变总数量)
取出3个黄球,放入3个红球
【问题六】如何比较随机事件发生的可能性大小?
比较随机事件发生的可能性大小时,可在相同的条件和总数一定的情况下,通过可能出现的结果数进行比较,结果数越多,则这个事件发生的可能性越大.
例2:如图,一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘.估计以下各事件的可能性大小,完成下列问题:
①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.
1)可能性最大的事件是_____,可能性最小的事件是_____(填序号);
2)将这些事件的序号按发生的可能性从小到大的顺序排列:________________.
④
②
② ③ ① ④
1.转动转盘,当转盘停止转动时,指针落在红色区域的可能性最大的是( )
2.下列4个袋子中,装有除颜色外完全相同的10个小球,任意摸出一个球,摸到红球可能性最大的是( )
例3 一个不透明的口袋中有6个红球,5个黄球,4个绿球,这些球除颜色外没有其它区别,现从中任意摸出一球,如果要使摸到绿球的可能性最大,需要在这个口袋中至少再放入多少个绿球?请简要说明理由.
解:至少再放入3个绿球.
理由:至少再放入3个绿球后,袋中有不少于7个绿球,即绿球的数量最多,这样摸到绿球的可能性最大.
1. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
1)当n为何值时,男生小强参加是确定事件?
2)当n为何值时,男生小强参加是随机事件?
【详解】1)若小强一定参加,则必须将所有男生都参加,
选4名同学参加,而男生共有3名,
∴女生只能参加1名,即n=1,此时男生小强参加是必然事件;
∴当n=4时,男生小强参加是不可能事件;
1. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
1)当n为何值时,男生小强参加是确定事件?
2)当n为何值时,男生小强参加是随机事件?
2)∵4名同学参加,而女生总共有5名,男生总共有3名,
∴男生最多参加2名,最少参加1名,
∴当n=2或3时,男生小强参加是随机事件.
1.(2023·湖北武汉·统考中考真题)掷两枚质地均匀的骰子,下列事件是随机事件的是( )
A.点数的和为1 B.点数的和为6
C.点数的和大于12 D.点数的和小于13
2.(2023·辽宁盘锦·统考中考真题)下列事件中,是必然事件的是( )
A.任意画一个三角形,其内角和是
B.任意买一张电影票,座位号是单号
C.掷一次骰子,向上一面的点数是3
D.射击运动员射击一次,命中靶心
1.通过本节课的学习,你学会了哪些知识?
2.你是怎样认识随机事件发生可能性大小的?
P128:练习
P129:练习
一套在手,备课无忧!
第25章 概率初步
25.1.1 随机概率
第五单元
1 理解必然事件、不可能事件、随机事件的概念,能辨别随机事件;
2 会简单分析事件发生的可能性;
3 经历体验、操作、观察、归纳、总结的过程,发展学生从复杂的表象中,提炼出本质特征并加以抽象概括的能力.
情景引入
探究新知
新知讲解
探究新知
典例分析
典例分析
针对训练
探究新知
新知讲解
针对训练
能力提升
直击中考
归纳小结
归纳小结
布置作业
下图为实际生活的具体现象,你觉得这些现象是否一定会发生?
太阳东升西落
天气预报显示
明天可能下雨
太阳绕着地球转
可能发生
一定发生
不可能发生
【问题一】小白、小黄、小花分别从箱1、箱2、箱3中各抽取一个球,一定能摸到红球吗?
箱1
箱3
箱2
不可能发生
可能发生
一定会发生
【问题二】 5名同学参加演讲比赛,以抽扑克牌的方式决定每个人的出场顺序.现桌面上有5张扑克牌(背面花色相同),牌面分别是1,2,3,4,5.小军首先抽签,他在看不到的扑克牌上数字的情况从桌面上随机(任意)地取一张扑克.
1)抽到的扑克牌有几种可能的结果?
2)抽到的扑克牌牌面数字会小于6吗?
3)抽到的扑克牌牌面数字会是0吗?
4)抽到的扑克牌牌面数字会是1吗?
五种可能,数字1-5都可能被抽到.
结果必然小于6.
结果不可能为0.
可能是1,也可能不是1,结果无法确定.
在一定条件下:
1)必然会发生的事件叫必然事件;
2)必然不会发生的事件叫不可能事件;
3)可能会发生,也可能不发生的事件叫不确定事件或随机事件.
【问题三】小伟掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1至6的点数.请考虑以下问题,掷一次骰子,观察骰子向上的一面:
1)可能出现哪些点数?
2) 出现的点数会是7吗?
3) 出现的点数大于0吗?
4) 出现的点数会是4吗?
5) 判断2)3)4)出现的事件属于哪种事件?
1,2,3,4,5,6
肯定不会是7.
肯定大于0.
出现点数可能是4,也可能不是4,结果无法确定.
2)为不可能事件
3)必然事件
4)随机事件
不可能事件
必然事件
确定性事件
随机事件
事件
1.确定性事件在事件发生前是可以预知结果的,即事件的发生或不发生具有必然性;
2.随机事件在事件发生前是不能预知结果的,也称为“偶然性事件”.
3.一般地,描述真理或客观存在的事实的事件是必然事件;描述违背真理或客观存在的事实的事件是不可能事件.
例1 判断下列事件属于哪种事件
1.将一小勺食盐放入开水中,食盐缓慢溶解.
2.测量某天的最高气温,结果为100℃.
3.小强打开电视机,电视里正在播放电视剧.
4.互为相反数的两个数的和等于0.
5.2019年2月的天数有29天.
必然事件
不可能事件
随机事件
必然事件
不可能事件
1. 下列事件中,①打开电视,它正在播关于扬州特产的广告;②太阳绕着地球转;③掷一枚正方体骰子,点数“4”朝上;④13人中至少有2人的生日是同一个月.属于随机事件的个数是 .
2. 一盒乒乓球中共有6只,其中2只次品,4只正品,正品和次品大小和形状完全相同,每次任取3只,出现了下列事件,指出这些事件分别是什么事件.
1)3只正品.
2)至少有一只次品.
3)3只次品.
4)至少有一只正品.
2
随机事件
随机事件
不可能事件
必然事件
小组讨论:
1.两人一组,两人轮流举事件,对方判断是什么事件;
2.两位同学讨论,全班交流,深化概念.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
1)这个球是白球还是黑球?
2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗并说明原因?
可能是白球,也可能是黑球.
不一样,黑球的数量大于白球数量,则摸出黑球的可能性大于白球的可能性.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
3)你能验证你的猜想吗?由此你发现了什么?
1.每名同学随机从袋子摸出一个球,记下球的颜色,并放回摇匀;
2.汇总全班的摸球结果,填在下表中.
球的颜色 黑球 白球
摸取次数
33
17
一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.
【问题四】袋中装有4个黑球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球.
4)能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
1.白球个数不变, 拿出两个黑球;
2.黑球个数不变,加入2个白球.
【问题五】能否通过改变盒中红、黄球的数量,在摸一个球的前提下,使“摸出红球”和“摸出黄球”的可能性大小相同?(不改变总数量)
取出3个黄球,放入3个红球
【问题六】如何比较随机事件发生的可能性大小?
比较随机事件发生的可能性大小时,可在相同的条件和总数一定的情况下,通过可能出现的结果数进行比较,结果数越多,则这个事件发生的可能性越大.
例2:如图,一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘.估计以下各事件的可能性大小,完成下列问题:
①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.
1)可能性最大的事件是_____,可能性最小的事件是_____(填序号);
2)将这些事件的序号按发生的可能性从小到大的顺序排列:________________.
④
②
② ③ ① ④
1.转动转盘,当转盘停止转动时,指针落在红色区域的可能性最大的是( )
2.下列4个袋子中,装有除颜色外完全相同的10个小球,任意摸出一个球,摸到红球可能性最大的是( )
例3 一个不透明的口袋中有6个红球,5个黄球,4个绿球,这些球除颜色外没有其它区别,现从中任意摸出一球,如果要使摸到绿球的可能性最大,需要在这个口袋中至少再放入多少个绿球?请简要说明理由.
解:至少再放入3个绿球.
理由:至少再放入3个绿球后,袋中有不少于7个绿球,即绿球的数量最多,这样摸到绿球的可能性最大.
1. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
1)当n为何值时,男生小强参加是确定事件?
2)当n为何值时,男生小强参加是随机事件?
【详解】1)若小强一定参加,则必须将所有男生都参加,
选4名同学参加,而男生共有3名,
∴女生只能参加1名,即n=1,此时男生小强参加是必然事件;
∴当n=4时,男生小强参加是不可能事件;
1. 某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
1)当n为何值时,男生小强参加是确定事件?
2)当n为何值时,男生小强参加是随机事件?
2)∵4名同学参加,而女生总共有5名,男生总共有3名,
∴男生最多参加2名,最少参加1名,
∴当n=2或3时,男生小强参加是随机事件.
1.(2023·湖北武汉·统考中考真题)掷两枚质地均匀的骰子,下列事件是随机事件的是( )
A.点数的和为1 B.点数的和为6
C.点数的和大于12 D.点数的和小于13
2.(2023·辽宁盘锦·统考中考真题)下列事件中,是必然事件的是( )
A.任意画一个三角形,其内角和是
B.任意买一张电影票,座位号是单号
C.掷一次骰子,向上一面的点数是3
D.射击运动员射击一次,命中靶心
1.通过本节课的学习,你学会了哪些知识?
2.你是怎样认识随机事件发生可能性大小的?
P128:练习
P129:练习
一套在手,备课无忧!
同课章节目录
