第12章 全等三角形 章末复习课件(36张PPT)
文档属性
| 名称 | 第12章 全等三角形 章末复习课件(36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 37.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 10:04:34 | ||
图片预览




文档简介
(共36张PPT)
第12章
全等三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
单元复盘提升
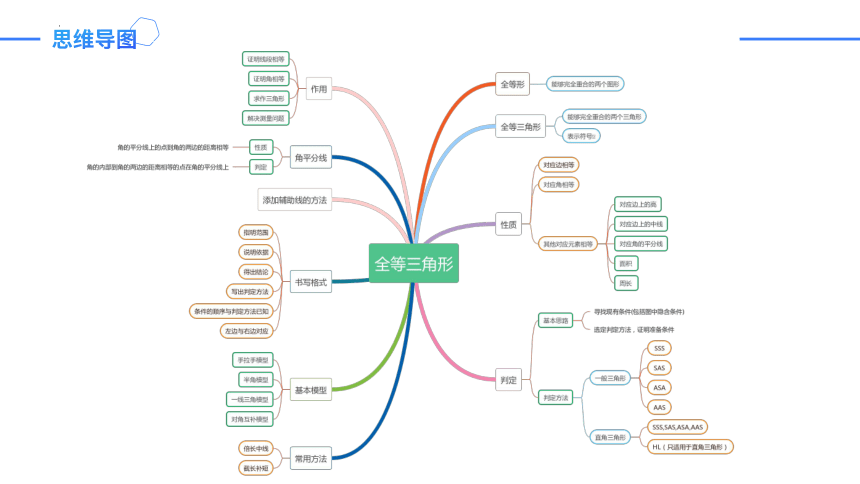
思维导图
知识串讲
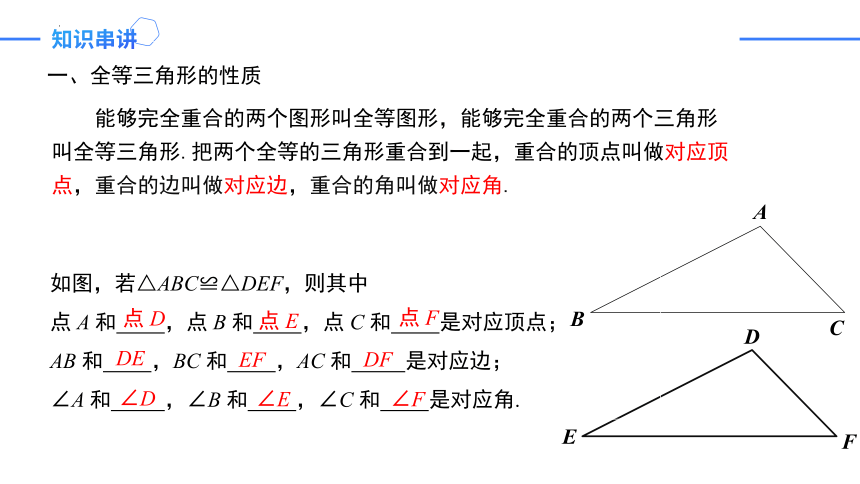
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
一、全等三角形的性质
B
C
E
F
如图,若△ABC≌△DEF,则其中
点 A 和 ,点 B 和 ,点 C 和 是对应顶点;
AB 和 ,BC 和 ,AC 和 是对应边;
∠A 和 ,∠B 和 ,∠C 和 是对应角.
A
D
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
知识串讲
A
B
C
D
E
F
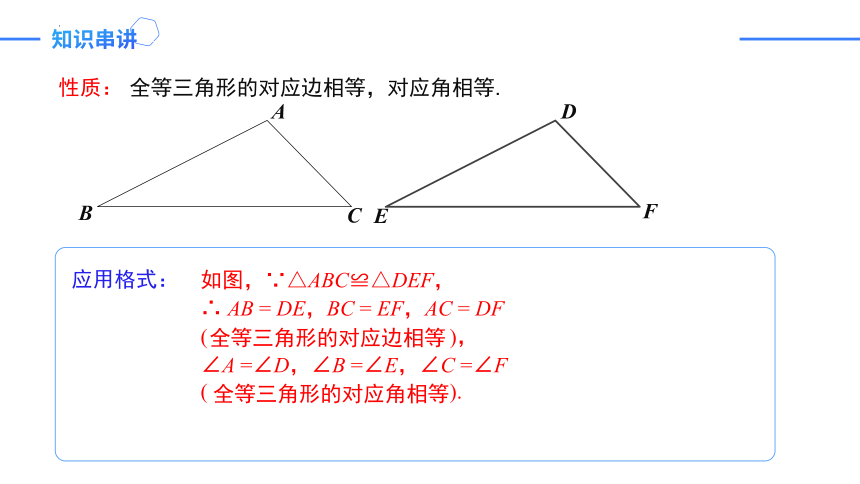
性质:
全等三角形的对应边相等,对应角相等.
如图,∵△ABC≌△DEF,
∴ AB = DE,BC = EF,AC = DF
( ),
∠A =∠D,∠B =∠E,∠C =∠F
( ).
全等三角形的对应边相等
全等三角形的对应角相等
应用格式:
知识串讲
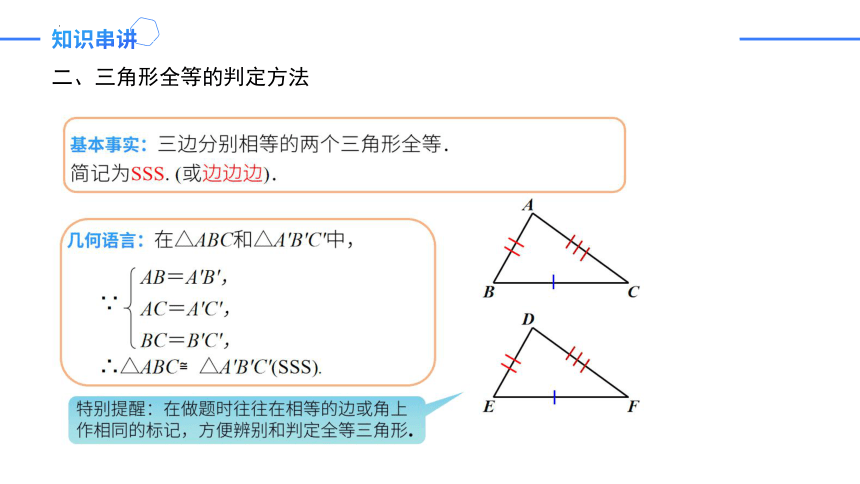
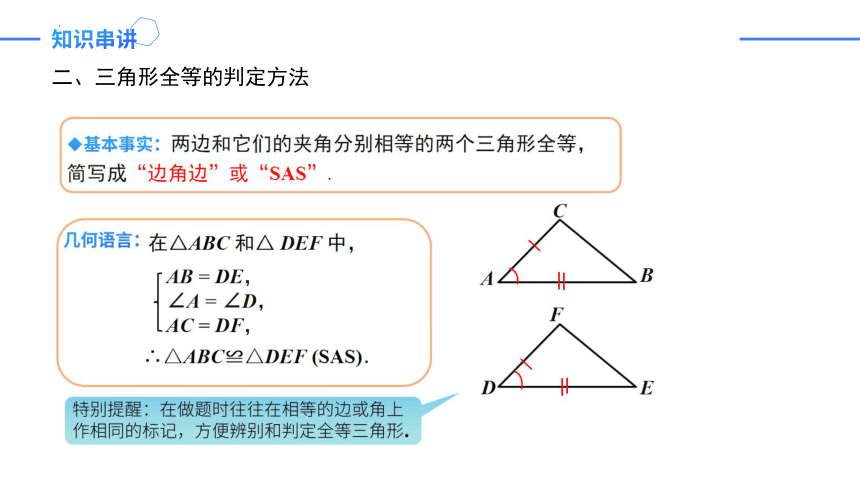
二、三角形全等的判定方法
知识串讲
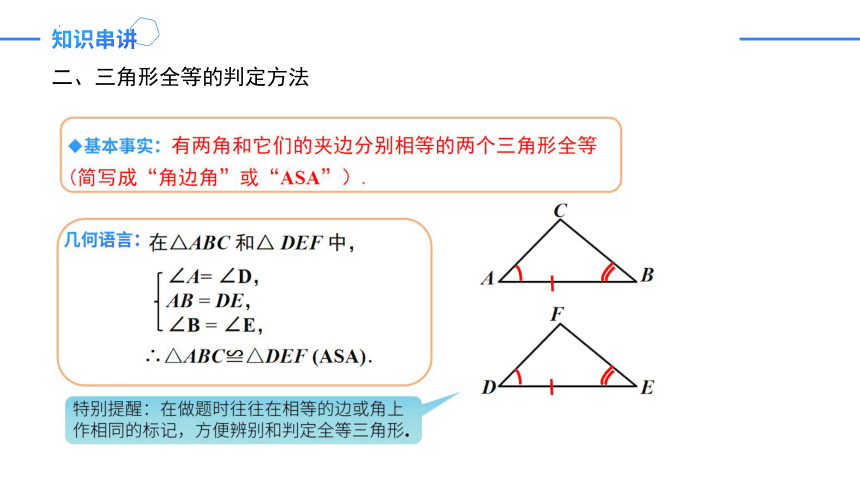
二、三角形全等的判定方法
知识串讲
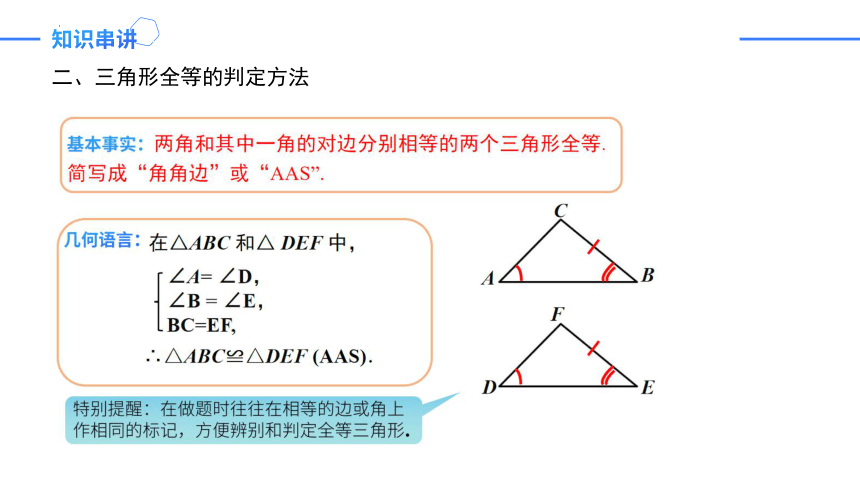
二、三角形全等的判定方法
知识串讲
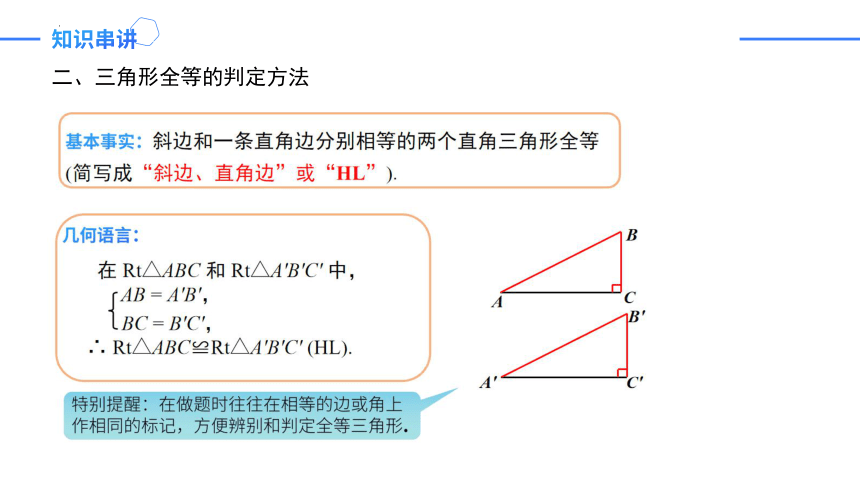
二、三角形全等的判定方法
知识串讲
二、三角形全等的判定方法
知识串讲
三、角平分线的性质与判定
考点梳理
考点一:全等三角形的性质
例1
已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,求EF边上的高.
解:∵△ABC≌△DEF,
∴△ABC的面积等于△DEF的面积.
∵EF=6cm,△DEF的面积为18cm2,
∴EF边上的高为6cm.
考点梳理
考点一:全等三角形的性质
例2
解:(1)∠BAE=∠CAD,理由如下:
∵△ABD≌△ACE, ∴∠BAD=∠CAE.
∵∠BAE=∠BAD+∠DAE,∠CAD=∠CAE+∠DAE,
∴∠BAD+∠DAE=∠CAE+∠DAE.
∴∠BAE=∠CAD.
如图,已知△ABD≌△ACE,点B、D、E、C在同一条直线上.
(1)∠BAE和∠CAD有什么关系?说明理由;
(2)BE与CD相等吗?请说明理由.
B
D
E
C
A
(2)BE=CD,理由如下:
∵△ABD≌△ACE, ∴BD=CE.
∵BE=BD+DE,CD=CE+DE,
∴BD+DE=CE+DE.
∴BE=CD.
刻意练习
练1
在△ABC中,∠A:∠ABC:∠ACB=3:5:10,△MNC≌△BAC,则∠BCN= ( )
A.10° B.20° C.50° D.80°
B
解:设 ∠A为3x,∠ABC为5x,∠ACB 为10x.
由三角形内角和得:3x+5x+10x=180° ,解得x=10° .
则 ∠A=30° ,∠ABC=50° ,∠ACB =100° .
∵△MNC≌△BAC,
∴∠M=∠ABC =50° ,∠N=∠A =30° ,
∠ACN=∠M+∠N =80° ,∠BCN=∠ACB-∠ACN=20° .
A
N
M
C
B
刻意练习
练2
解:∵∠ACB=105°,∠B=50°,
∴∠CAB=180°-∠B-∠ACB=25°.
∵ △ABC≌△ADE,
∴∠EAD=∠CAB=25°.
又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=10°,
∴∠AEB=180°-∠EAB-∠B=70°.
∴∠DEF=∠AED-∠AEB=35°.
如图,已知△ABC≌△ADE,BC的延长线过点E,交AD于点F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF的度数.
A
C
E
D
F
B
考点梳理
考点二:全等三角形的判定综合
例3
如图,O是线段AB和线段CD的中点.求证:(1)△AOD≌△BOC;(2)AD∥BC.
考点梳理
考点二:全等三角形的判定综合
例4
如图, 在△ABC和△DEF中, 点B,E, C, F在同一直线上, 下面有四个条件, 请你从中选三个作为题设, 余下的一个作为结论, 写出一个正确的命题, 并加以证明.
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
考点梳理
考点二:全等三角形的判定综合
例4
条件 结论 是否正确 依据
②③④ ① 不正确 由“SSA”不能得出△ABC与△DEF全等
①③④ ② 正确 由“SAS”得△ABC≌△DEF
①②④ ③ 正确 由“SSS”得△ABC≌△DEF
①②③ ④ 不正确 由“SSA”不能得出△ABC与△DEF全等
考点梳理
考点二:全等三角形的判定综合
例5
如图,在△ABC 中,AD 平分∠BAC,CE⊥AD 于点 G,交 AB 于点 E,EF∥BC 交 AC 于点 F.求证:∠DEC =∠FEC.
A
B
C
D
F
E
G
证明:∵ CE⊥AD,∴∠AGE =∠AGC = 90°.
在△AGE 和△AGC 中,
∠AGE =∠AGC,
AG = AG,
∠EAG =∠CAG,
∵ AD 平分∠BAC,∴∠EAG =∠CAG.
∴△AGE≌△AGC (ASA).
∴ GE = GC.
考点梳理
考点二:全等三角形的判定综合
例5
在△DGE 和△DGC 中,
EG = CG,
∠EGD =∠CGD,
DG = DG,
∴△DGE≌△DGC (SAS).
∴∠DEG = ∠DCG.
∵ EF∥BC,
∴∠FEC = ∠DCG.
∴∠DEG = ∠FEC.
A
B
C
D
F
E
G
考点梳理
考点二:全等三角形的判定综合
例6
如图,已知△ABC中,AB=AC=10,BC=8,点D为AB的中点,点P在线段BC上以每秒3个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以每秒a个单位长度的速度运动,设运动时间为t秒.
(1)求CP的长(用含有t的式子表示);
C
A
B
Q
D
P
解:(1)由题意得:BP=3t.
∵BC=8, ∴CP=BC-BP=8-3t.
考点梳理
考点二:全等三角形的判定综合
例6
(2)若以点C、P、Q为顶点的三角形和以点B、D、P为顶点的三角形全等,且∠B和∠C是对应角,求a和t的值.
C
A
B
Q
D
P
解:(2)①若△BDP≌△CPQ,∵AB=10,点D为AB的中点,∴ BD=5.
根据题意:BP=3t,CP=8-3t,CQ=at. ∵△BDP≌△CPQ,
∴BD=CP,BP=CQ,∴5=8-3t,3t=at,解得t=1,a=3.
②若△BDP≌△CQP,∵AB=10,点D为AB的中点,
∴ BD=5.根据题意:BP=3t,CP=8-3t,CQ=at.
∵△BDP≌△CQP, ∴BP=CP,BD=CQ.
∴3t=8-3t,5=at,解得t=4/3 ,a=15/4 .
刻意练习
练3
如图, 点C, F, E, B在一条直线上, ∠CFD= ∠BEA, CE=BF, DF=AE.写出CD与AB之间的关系,并证明你的结论.
刻意练习
练4
如图, 在△ACD和△ABE中, 点D在AB上, 点E在AC上. 下面四个条件中, 请你以其中两个为题设, 一个为结论, 写出一个真命题(只需写出一种情况), 并证明.①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
刻意练习
练5
如图, AB⊥CD, 且AB=CD. E, F是AD上两点, CE⊥AD, BF⊥AD.若CE=a, BF=b, EF=c, 则AD的长为( ).
A.a+c B.b+c
C.a-b+c D.a+b-c
D
分析 ∵AB⊥CD, CE⊥AD, BF⊥AD,
∴∠AFB=∠CED=90°, ∠A+∠D=90°,
∠C+∠D=90°,∴∠A=∠C.
又∵AB=CD, ∴△ABF≌△CDE,
∴AF=CE=a, BF=DE=b.∵EF=c,
∴AD=AF+DF=a+(b-c)=a+b-c.故选D.
刻意练习
练6
如图, 已知AB=AD, AC=AE, ∠BAE=∠DAC. 求证:∠C=∠E.
考点梳理
考点三:利用全等三角形解决实际问题
例7
如图所示, 小强在河的一岸, 要测量河面一只船B与对岸码头A的距离, 他的做法如下:①在岸边确定一点C, 使C与A, B在同一直线上;②在与AC垂直的方向画线段CD, 取其中点O; ③画DF⊥CD, 使F, O, A在同一直线上;④在线段DF上找到一点E, 使E与O, B共线. 他说测出线段FE
的长就是船B与码头A的距离. 他
这样做有道理吗?为什么?
考点梳理
考点三:利用全等三角形解决实际问题
例7
解:小强这样做有道理. 理由:
∵AC⊥CD, DF⊥CD,∴∠C=∠D=90°.
又∵OC=OD, ∠AOC=∠FOD(对顶角相等),
∴△ACO≌△FDO(ASA),
∴OA=OF, ∠A=∠F(全等三角形的对应边相等, 对应角相等).
又∵∠AOB=∠FOE(对顶角相等),
∴△AOB≌△FOE(ASA),
∴AB=FE(全等三角形的对应边相等),
∴线段FE的长就是船B与码头A的距离.
刻意练习
练7
解:∵△AEF是由△AED沿直线AE折叠而成,
∴△ADE≌△AFE,
∴∠DAE=∠FAE.
∵∠BAF=56°, ∠BAD=90°,
∴∠DAF=90°-∠BAF=90°-56°=34°,
∴∠DAE= ∠DAF= ×34°=17°.
如图, 将长方形纸片ABCD沿AE折叠, 使点D落在BC边上的点F处. 若∠BAF=56°, 求∠DAE的度数.
考点梳理
考点四:角平分线的性质与判定
例8
如图, ∠B=∠C=90°, E是BC的中点, DE平分∠ADC.求证:AD=AB+CD.
刻意练习
练8
如图, ∠B=∠C=90°, E是BC的中点, DE平分∠ADC, ∠CED=35°,
则∠EAB的度数是( ).
A.35° B.45°
C.55° D.65°
A
刻意练习
练9
如图,∠1=∠2,点 P 为 BN 上的一点,PA = PC.
求证:∠PCB +∠BAP = 180°.
B
A
C
N
)
)
1
2
P
E
F
证明:过点 P 作 PE⊥BA,PF⊥BC,垂足分别为 E,F.
又∵∠1 =∠2,
∴PE = PF, ∠PEA =∠PFC = 90°.
PA = PC,
PE = PF,
在Rt△APE 和Rt△CPF 中,
∴ Rt△PAE≌Rt△PCF (HL).
∴∠EAP =∠FCP =∠PCB.
∵∠BAP +∠EAP = 180°,
∴∠PCB +∠BAP = 180°.
模型总结
模型一:
模型总结
模型二:
模型总结
模型三:
课程小结
判定
作用
是证明两条线段相等和角相等的常用方法
判定方法基本思路:
寻找现有条件(包括图中隐含条件);
选定判定方法,证明准备条件.
判定方法:SSS,SAS,ASA,AAS,HL
全等三角形
对应元素相等
性质
性质与判定
角平分线
第12章
全等三角形
八年级数学上册同步精品课堂(人教版)
人教版 数学
八年级 上册
单元复盘提升
思维导图
知识串讲
能够完全重合的两个图形叫全等图形,能够完全重合的两个三角形叫全等三角形.把两个全等的三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
一、全等三角形的性质
B
C
E
F
如图,若△ABC≌△DEF,则其中
点 A 和 ,点 B 和 ,点 C 和 是对应顶点;
AB 和 ,BC 和 ,AC 和 是对应边;
∠A 和 ,∠B 和 ,∠C 和 是对应角.
A
D
点 D
点 E
点 F
DE
EF
DF
∠D
∠E
∠F
知识串讲
A
B
C
D
E
F
性质:
全等三角形的对应边相等,对应角相等.
如图,∵△ABC≌△DEF,
∴ AB = DE,BC = EF,AC = DF
( ),
∠A =∠D,∠B =∠E,∠C =∠F
( ).
全等三角形的对应边相等
全等三角形的对应角相等
应用格式:
知识串讲
二、三角形全等的判定方法
知识串讲
二、三角形全等的判定方法
知识串讲
二、三角形全等的判定方法
知识串讲
二、三角形全等的判定方法
知识串讲
二、三角形全等的判定方法
知识串讲
三、角平分线的性质与判定
考点梳理
考点一:全等三角形的性质
例1
已知△ABC≌△DEF,BC=EF=6cm,△ABC的面积为18cm2,求EF边上的高.
解:∵△ABC≌△DEF,
∴△ABC的面积等于△DEF的面积.
∵EF=6cm,△DEF的面积为18cm2,
∴EF边上的高为6cm.
考点梳理
考点一:全等三角形的性质
例2
解:(1)∠BAE=∠CAD,理由如下:
∵△ABD≌△ACE, ∴∠BAD=∠CAE.
∵∠BAE=∠BAD+∠DAE,∠CAD=∠CAE+∠DAE,
∴∠BAD+∠DAE=∠CAE+∠DAE.
∴∠BAE=∠CAD.
如图,已知△ABD≌△ACE,点B、D、E、C在同一条直线上.
(1)∠BAE和∠CAD有什么关系?说明理由;
(2)BE与CD相等吗?请说明理由.
B
D
E
C
A
(2)BE=CD,理由如下:
∵△ABD≌△ACE, ∴BD=CE.
∵BE=BD+DE,CD=CE+DE,
∴BD+DE=CE+DE.
∴BE=CD.
刻意练习
练1
在△ABC中,∠A:∠ABC:∠ACB=3:5:10,△MNC≌△BAC,则∠BCN= ( )
A.10° B.20° C.50° D.80°
B
解:设 ∠A为3x,∠ABC为5x,∠ACB 为10x.
由三角形内角和得:3x+5x+10x=180° ,解得x=10° .
则 ∠A=30° ,∠ABC=50° ,∠ACB =100° .
∵△MNC≌△BAC,
∴∠M=∠ABC =50° ,∠N=∠A =30° ,
∠ACN=∠M+∠N =80° ,∠BCN=∠ACB-∠ACN=20° .
A
N
M
C
B
刻意练习
练2
解:∵∠ACB=105°,∠B=50°,
∴∠CAB=180°-∠B-∠ACB=25°.
∵ △ABC≌△ADE,
∴∠EAD=∠CAB=25°.
又∵∠EAB=∠EAD+∠CAD+∠CAB,∠CAD=10°,
∴∠AEB=180°-∠EAB-∠B=70°.
∴∠DEF=∠AED-∠AEB=35°.
如图,已知△ABC≌△ADE,BC的延长线过点E,交AD于点F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF的度数.
A
C
E
D
F
B
考点梳理
考点二:全等三角形的判定综合
例3
如图,O是线段AB和线段CD的中点.求证:(1)△AOD≌△BOC;(2)AD∥BC.
考点梳理
考点二:全等三角形的判定综合
例4
如图, 在△ABC和△DEF中, 点B,E, C, F在同一直线上, 下面有四个条件, 请你从中选三个作为题设, 余下的一个作为结论, 写出一个正确的命题, 并加以证明.
①AB=DE;②AC=DF;③∠ABC=∠DEF;④BE=CF.
考点梳理
考点二:全等三角形的判定综合
例4
条件 结论 是否正确 依据
②③④ ① 不正确 由“SSA”不能得出△ABC与△DEF全等
①③④ ② 正确 由“SAS”得△ABC≌△DEF
①②④ ③ 正确 由“SSS”得△ABC≌△DEF
①②③ ④ 不正确 由“SSA”不能得出△ABC与△DEF全等
考点梳理
考点二:全等三角形的判定综合
例5
如图,在△ABC 中,AD 平分∠BAC,CE⊥AD 于点 G,交 AB 于点 E,EF∥BC 交 AC 于点 F.求证:∠DEC =∠FEC.
A
B
C
D
F
E
G
证明:∵ CE⊥AD,∴∠AGE =∠AGC = 90°.
在△AGE 和△AGC 中,
∠AGE =∠AGC,
AG = AG,
∠EAG =∠CAG,
∵ AD 平分∠BAC,∴∠EAG =∠CAG.
∴△AGE≌△AGC (ASA).
∴ GE = GC.
考点梳理
考点二:全等三角形的判定综合
例5
在△DGE 和△DGC 中,
EG = CG,
∠EGD =∠CGD,
DG = DG,
∴△DGE≌△DGC (SAS).
∴∠DEG = ∠DCG.
∵ EF∥BC,
∴∠FEC = ∠DCG.
∴∠DEG = ∠FEC.
A
B
C
D
F
E
G
考点梳理
考点二:全等三角形的判定综合
例6
如图,已知△ABC中,AB=AC=10,BC=8,点D为AB的中点,点P在线段BC上以每秒3个单位长度的速度由点B向点C运动,同时点Q在线段CA上由点C向点A以每秒a个单位长度的速度运动,设运动时间为t秒.
(1)求CP的长(用含有t的式子表示);
C
A
B
Q
D
P
解:(1)由题意得:BP=3t.
∵BC=8, ∴CP=BC-BP=8-3t.
考点梳理
考点二:全等三角形的判定综合
例6
(2)若以点C、P、Q为顶点的三角形和以点B、D、P为顶点的三角形全等,且∠B和∠C是对应角,求a和t的值.
C
A
B
Q
D
P
解:(2)①若△BDP≌△CPQ,∵AB=10,点D为AB的中点,∴ BD=5.
根据题意:BP=3t,CP=8-3t,CQ=at. ∵△BDP≌△CPQ,
∴BD=CP,BP=CQ,∴5=8-3t,3t=at,解得t=1,a=3.
②若△BDP≌△CQP,∵AB=10,点D为AB的中点,
∴ BD=5.根据题意:BP=3t,CP=8-3t,CQ=at.
∵△BDP≌△CQP, ∴BP=CP,BD=CQ.
∴3t=8-3t,5=at,解得t=4/3 ,a=15/4 .
刻意练习
练3
如图, 点C, F, E, B在一条直线上, ∠CFD= ∠BEA, CE=BF, DF=AE.写出CD与AB之间的关系,并证明你的结论.
刻意练习
练4
如图, 在△ACD和△ABE中, 点D在AB上, 点E在AC上. 下面四个条件中, 请你以其中两个为题设, 一个为结论, 写出一个真命题(只需写出一种情况), 并证明.①AE=AD;②AB=AC;③OB=OC;④∠B=∠C.
刻意练习
练5
如图, AB⊥CD, 且AB=CD. E, F是AD上两点, CE⊥AD, BF⊥AD.若CE=a, BF=b, EF=c, 则AD的长为( ).
A.a+c B.b+c
C.a-b+c D.a+b-c
D
分析 ∵AB⊥CD, CE⊥AD, BF⊥AD,
∴∠AFB=∠CED=90°, ∠A+∠D=90°,
∠C+∠D=90°,∴∠A=∠C.
又∵AB=CD, ∴△ABF≌△CDE,
∴AF=CE=a, BF=DE=b.∵EF=c,
∴AD=AF+DF=a+(b-c)=a+b-c.故选D.
刻意练习
练6
如图, 已知AB=AD, AC=AE, ∠BAE=∠DAC. 求证:∠C=∠E.
考点梳理
考点三:利用全等三角形解决实际问题
例7
如图所示, 小强在河的一岸, 要测量河面一只船B与对岸码头A的距离, 他的做法如下:①在岸边确定一点C, 使C与A, B在同一直线上;②在与AC垂直的方向画线段CD, 取其中点O; ③画DF⊥CD, 使F, O, A在同一直线上;④在线段DF上找到一点E, 使E与O, B共线. 他说测出线段FE
的长就是船B与码头A的距离. 他
这样做有道理吗?为什么?
考点梳理
考点三:利用全等三角形解决实际问题
例7
解:小强这样做有道理. 理由:
∵AC⊥CD, DF⊥CD,∴∠C=∠D=90°.
又∵OC=OD, ∠AOC=∠FOD(对顶角相等),
∴△ACO≌△FDO(ASA),
∴OA=OF, ∠A=∠F(全等三角形的对应边相等, 对应角相等).
又∵∠AOB=∠FOE(对顶角相等),
∴△AOB≌△FOE(ASA),
∴AB=FE(全等三角形的对应边相等),
∴线段FE的长就是船B与码头A的距离.
刻意练习
练7
解:∵△AEF是由△AED沿直线AE折叠而成,
∴△ADE≌△AFE,
∴∠DAE=∠FAE.
∵∠BAF=56°, ∠BAD=90°,
∴∠DAF=90°-∠BAF=90°-56°=34°,
∴∠DAE= ∠DAF= ×34°=17°.
如图, 将长方形纸片ABCD沿AE折叠, 使点D落在BC边上的点F处. 若∠BAF=56°, 求∠DAE的度数.
考点梳理
考点四:角平分线的性质与判定
例8
如图, ∠B=∠C=90°, E是BC的中点, DE平分∠ADC.求证:AD=AB+CD.
刻意练习
练8
如图, ∠B=∠C=90°, E是BC的中点, DE平分∠ADC, ∠CED=35°,
则∠EAB的度数是( ).
A.35° B.45°
C.55° D.65°
A
刻意练习
练9
如图,∠1=∠2,点 P 为 BN 上的一点,PA = PC.
求证:∠PCB +∠BAP = 180°.
B
A
C
N
)
)
1
2
P
E
F
证明:过点 P 作 PE⊥BA,PF⊥BC,垂足分别为 E,F.
又∵∠1 =∠2,
∴PE = PF, ∠PEA =∠PFC = 90°.
PA = PC,
PE = PF,
在Rt△APE 和Rt△CPF 中,
∴ Rt△PAE≌Rt△PCF (HL).
∴∠EAP =∠FCP =∠PCB.
∵∠BAP +∠EAP = 180°,
∴∠PCB +∠BAP = 180°.
模型总结
模型一:
模型总结
模型二:
模型总结
模型三:
课程小结
判定
作用
是证明两条线段相等和角相等的常用方法
判定方法基本思路:
寻找现有条件(包括图中隐含条件);
选定判定方法,证明准备条件.
判定方法:SSS,SAS,ASA,AAS,HL
全等三角形
对应元素相等
性质
性质与判定
角平分线
