3.7探索与表达规律二课件
图片预览


文档简介
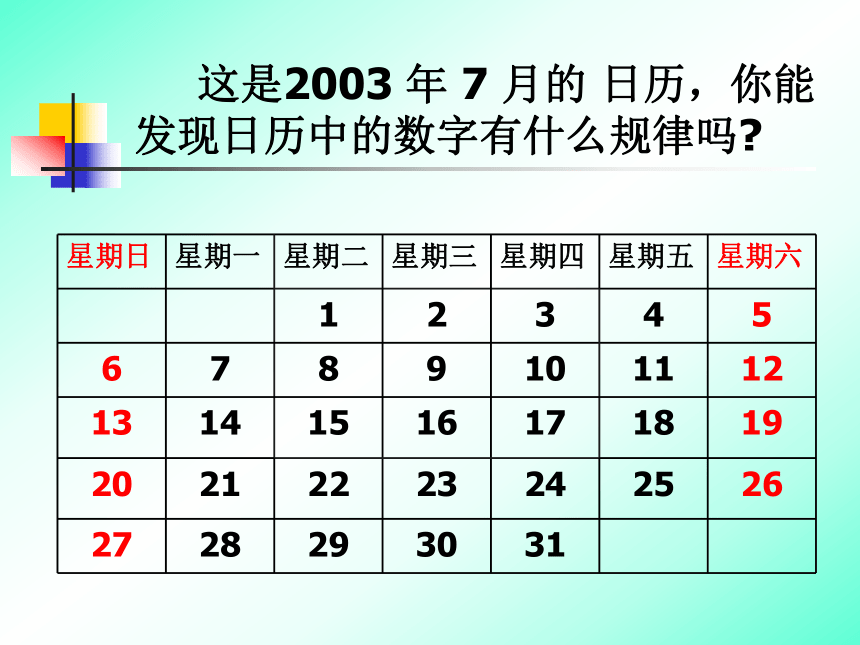
课件39张PPT。探 索与表达 规 律 这是2003 年 7 月的 日历,你能发现日历中的数字有什么规律吗?经历探索数量关系、运用符号表示规 律、通过运算验证规律的过程。
2.会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
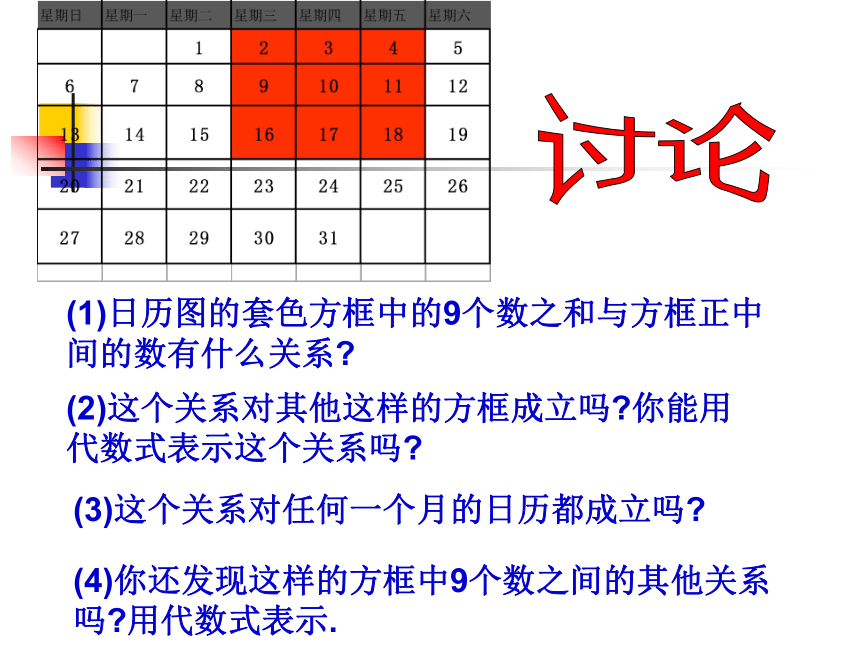
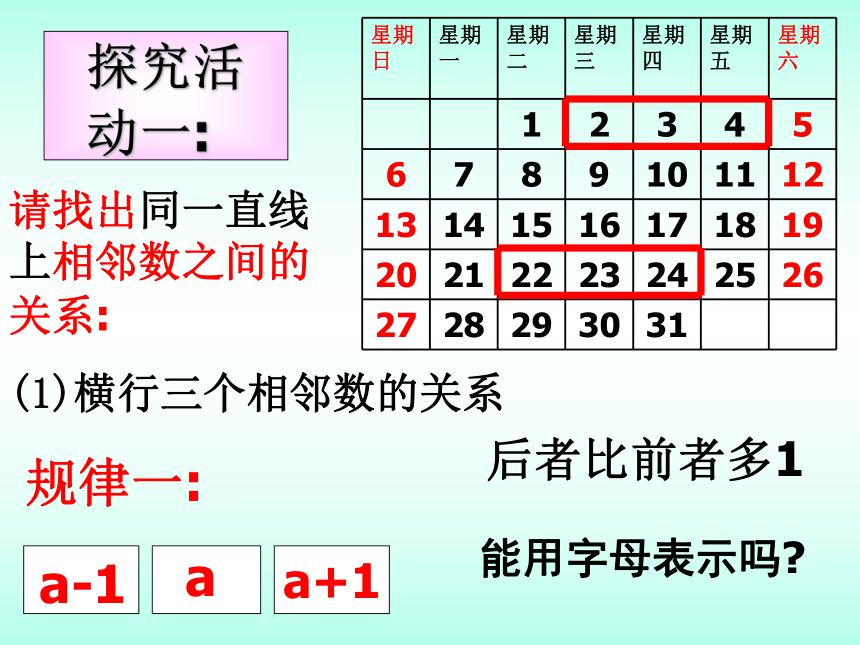
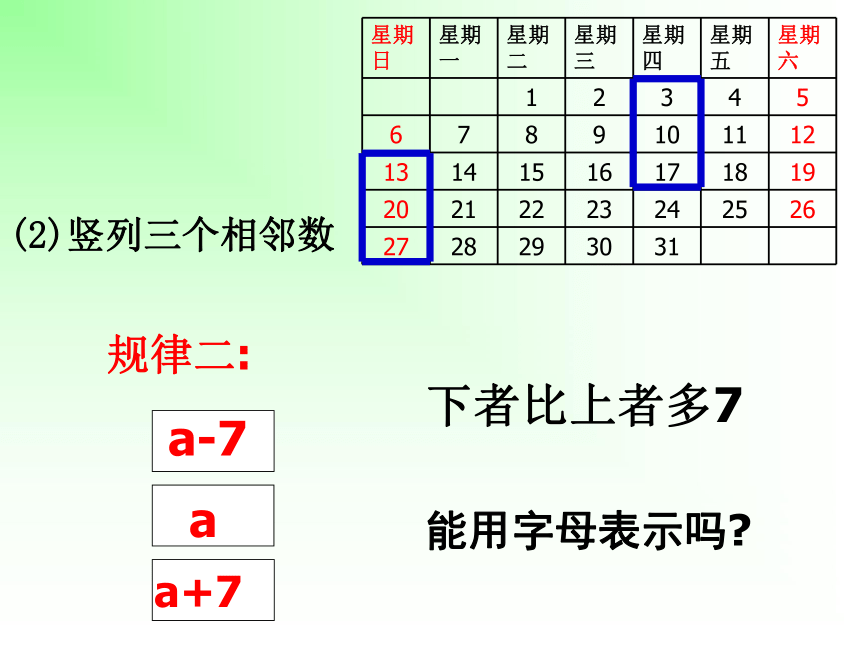
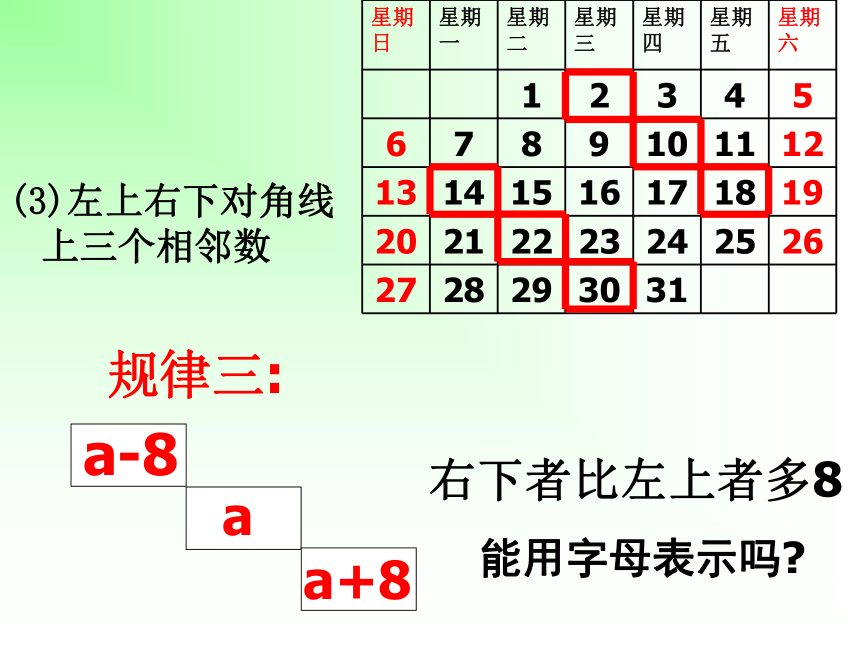
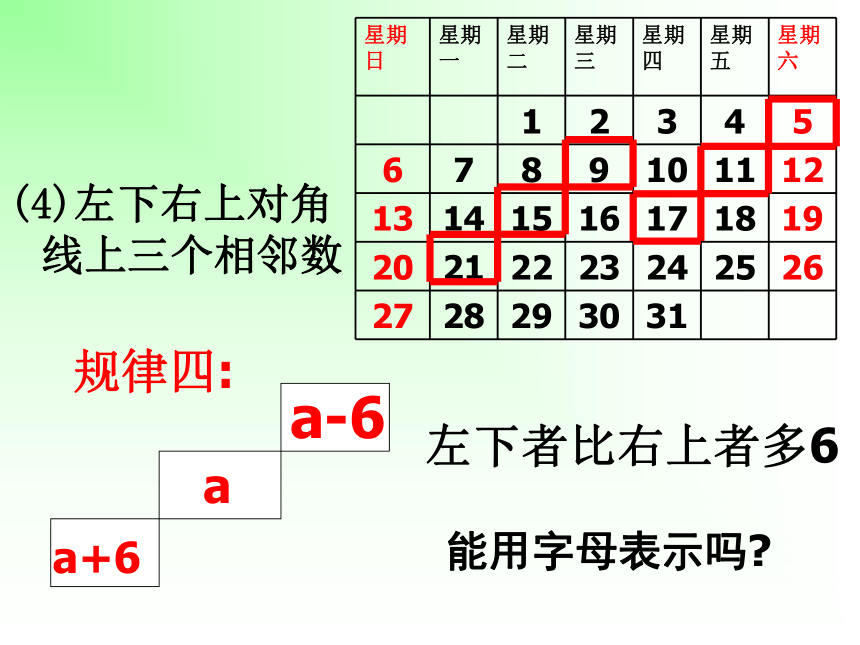
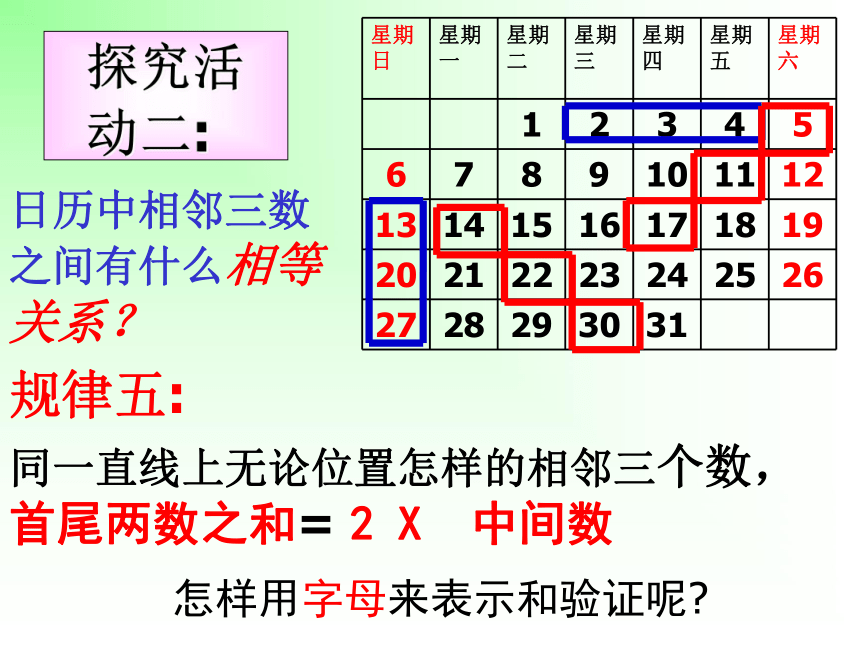
3.积极思考,踊跃发言,大胆地交流你所探索的规律。学习目标(1)日历图的套色方框中的9个数之和与方框正中间的数有什么关系?(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?(3)这个关系对任何一个月的日历都成立吗?(4)你还发现这样的方框中9个数之间的其他关系吗?用代数式表示.讨论请找出同一直线上相邻数之间的关系:横行三个相邻数的关系后者比前者多1能用字母表示吗?探究活动一:(2)竖列三个相邻数下者比上者多7能用字母表示吗?(3)左上右下对角线上三个相邻数右下者比左上者多8能用字母表示吗?(4)左下右上对角线上三个相邻数左下者比右上者多6能用字母表示吗?日历中相邻三数之间有什么相等关系?怎样用字母来表示和验证呢?探究活动二:(1) 水平三邻数: (2)竖直三邻数:(3)斜下三邻数:(4)斜上三邻数(a-1)+(a+1)=___2a(a-7)+(a+7)
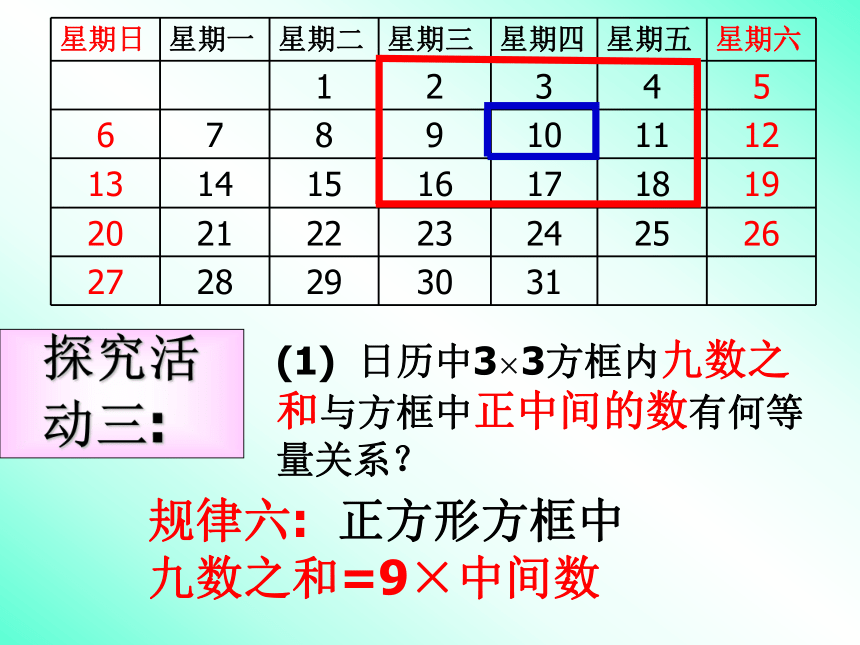
=____2a(a-8)+(a+8)=____2a(a-6)+(a+6)=_____2a 在日历中,同一直线上无论位置怎样的相邻三个数,首尾两数之和都等于中间数的2倍。注意哦! 对探索到的规律既要能用文字叙述它,又要会用字母来表示和验证它!(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?规律六: 正方形方框中 九数之和=9×中间数 这个关系在其它方框中成立吗?答:成立!(3) 这个关系对任何一个月的日历都成立吗?2003 年 2 月 日历答:成立!2003 年 2 月 日历(4) 这个规律也能用字母表示吗?aa-7a+8a-6a-8a+6a+7a-1a+1(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)
(a+6)+(a+7)+(a+8) = ______9a 在正方形方框中,设中间的一个数为a,那么,其余八个数分别应怎样表示?所以,正方形方框中,九数之和等于中间数的九倍。(5) 你还能发现正方形方框中九数之间的其它关系吗?变式探究巩固提高2003 年 7 月 日历变式探究(1) 在 + 字形区域内,五个数之和与正中心何关系? 能用字母表示并验证这个关系吗?答:五数之和=5×中间数aa+1a-1a+7a-7(a-1)+(a+1)+a+(a-7)+(a+7)=___5a想一想(1)如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?(2)你还能设计其他形状的包含数字规律的数框吗?2003 年 7 月 日历变式探究(2) 在 H 形区域内,七个数之和与正中心的数有关系? 能用字母表示吗?答:七数之和=7×中间数aa-1a+1a-8a+6a-6a+8(a-8)+(a+8)+(a-1)+(a+1)
+a+(a-6)+(a+6)= 7a小 结 通过本节课你有哪些收获? 3 5 7 9 11
15 17 19 21 23
27 29 31 33 35
37 39 41 43 45 47将连续的奇数1、3、5、7…排成如下的数表,十字框中的5个数中:
(1)中间的数17与这5个数的和有什么关系?(2)将十字框上下左右移动,可以框住另外的5个数,还有这种关系吗?
(3)设中间的数为a,用代数式表示十字框中的5个数的和。
变式练习二(1)在下列表格中前面所探究的规律是否正确?变式思考,灵活选用: (2)在下列表格中前面所探究的规律
是否正确? 你还能发现哪些规律?你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5最后得到的数加个位数。把你的结果告诉我,我就知道你心里想的两位数。知道为什么吗?
比如你想的数是15,1x2+3=5,5x5=25,25+5=30
又如12,1x2+3=5,5x5=25,25+2=27你发现了什么规律?是不是你用你所想的数算的结果总比你想的数大15?不信你用其他的两位数试试细胞分裂问题细胞每次都是由一个分裂成两个。24816212223242n…我们曾经接触过“细胞分裂”问题:思路启迪 ? 可从具体的、简单的对折次数入手,寻找 所得折痕数与对折次数的变化关系. 13715…24816…212223242n2n-1 将一张长方形的纸对折,如右图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折n次后,可以得到多少条折痕?折 纸 问 题谁能算出:1+2+22+23+24+……2n=?
13715…24816…212223242n2n-1观察上表可得: 1=21- 1 3=1+ 21 =22- 1
7=1+21 +22 =23- 1
15= 1+21 +22 +23=24- 1……所以 1+2+22+23+24+……2n=
2n+1-1+2+4+8探索规律的一般步骤:猜 想 规 律表 示 规 律验 证 规 律具 体 问 题观 察 特 例成立得出结论头 回新 重索 探智慧园1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 x 10 5 1
1 6 y 20 15 6 1
观察下表,找出规律:根据表中的规律,可知x = ,y = .1015等分次数(n)正方形个数(s)=3+1=2×3+1=3×3+1=4×3+1思维拓展
①根据上述规律你知道第2003次操作后能将原来的正方形纸板剪成多少个正方形纸板?
②请你推断,能不能按上述操作过程,将原来的正方形纸板剪成33个正方形?为什么?① S2003=3×2003 + 1=60101.观察下列各式,你会发现什么规律?
3×5=15,而15=42-1;
5×7=35,而35=62-1;
11×13=143,而143=122-1;
……
请你猜想到的规律用只含一个字母的式子表示出来: .2.观察下列顺序排列的等式:
9×0+1=1,
9×1+2=11,
9×2+3=21,
9×3+4=31,
9×4+5=41,
……
猜想:第n个等式(n为正整数)应为 .3.观察下列各式:
1×3=12+2×1,
2×4=22+2×2,
3×5=32+2×3,
……
请你将猜想到的规律用自然数n(n≥1)表示出来: .
2.会用代数式表示简单问题中的数量关系,能用合并同类项、去括号等法则验证所探索的规律。
3.积极思考,踊跃发言,大胆地交流你所探索的规律。学习目标(1)日历图的套色方框中的9个数之和与方框正中间的数有什么关系?(2)这个关系对其他这样的方框成立吗?你能用代数式表示这个关系吗?(3)这个关系对任何一个月的日历都成立吗?(4)你还发现这样的方框中9个数之间的其他关系吗?用代数式表示.讨论请找出同一直线上相邻数之间的关系:横行三个相邻数的关系后者比前者多1能用字母表示吗?探究活动一:(2)竖列三个相邻数下者比上者多7能用字母表示吗?(3)左上右下对角线上三个相邻数右下者比左上者多8能用字母表示吗?(4)左下右上对角线上三个相邻数左下者比右上者多6能用字母表示吗?日历中相邻三数之间有什么相等关系?怎样用字母来表示和验证呢?探究活动二:(1) 水平三邻数: (2)竖直三邻数:(3)斜下三邻数:(4)斜上三邻数(a-1)+(a+1)=___2a(a-7)+(a+7)
=____2a(a-8)+(a+8)=____2a(a-6)+(a+6)=_____2a 在日历中,同一直线上无论位置怎样的相邻三个数,首尾两数之和都等于中间数的2倍。注意哦! 对探索到的规律既要能用文字叙述它,又要会用字母来表示和验证它!(1) 日历中3×3方框内九数之和与方框中正中间的数有何等量关系?规律六: 正方形方框中 九数之和=9×中间数 这个关系在其它方框中成立吗?答:成立!(3) 这个关系对任何一个月的日历都成立吗?2003 年 2 月 日历答:成立!2003 年 2 月 日历(4) 这个规律也能用字母表示吗?aa-7a+8a-6a-8a+6a+7a-1a+1(a-8)+(a-7)+(a-6)+(a-1)+a+(a+1)
(a+6)+(a+7)+(a+8) = ______9a 在正方形方框中,设中间的一个数为a,那么,其余八个数分别应怎样表示?所以,正方形方框中,九数之和等于中间数的九倍。(5) 你还能发现正方形方框中九数之间的其它关系吗?变式探究巩固提高2003 年 7 月 日历变式探究(1) 在 + 字形区域内,五个数之和与正中心何关系? 能用字母表示并验证这个关系吗?答:五数之和=5×中间数aa+1a-1a+7a-7(a-1)+(a+1)+a+(a-7)+(a+7)=___5a想一想(1)如果将方框改为十字形框,你能发现哪些规律?如果改为“H”形框呢?(2)你还能设计其他形状的包含数字规律的数框吗?2003 年 7 月 日历变式探究(2) 在 H 形区域内,七个数之和与正中心的数有关系? 能用字母表示吗?答:七数之和=7×中间数aa-1a+1a-8a+6a-6a+8(a-8)+(a+8)+(a-1)+(a+1)
+a+(a-6)+(a+6)= 7a小 结 通过本节课你有哪些收获? 3 5 7 9 11
15 17 19 21 23
27 29 31 33 35
37 39 41 43 45 47将连续的奇数1、3、5、7…排成如下的数表,十字框中的5个数中:
(1)中间的数17与这5个数的和有什么关系?(2)将十字框上下左右移动,可以框住另外的5个数,还有这种关系吗?
(3)设中间的数为a,用代数式表示十字框中的5个数的和。
变式练习二(1)在下列表格中前面所探究的规律是否正确?变式思考,灵活选用: (2)在下列表格中前面所探究的规律
是否正确? 你还能发现哪些规律?你在心里想好一个两位数,将十位数字乘2,然后加3,再将所得新数乘5最后得到的数加个位数。把你的结果告诉我,我就知道你心里想的两位数。知道为什么吗?
比如你想的数是15,1x2+3=5,5x5=25,25+5=30
又如12,1x2+3=5,5x5=25,25+2=27你发现了什么规律?是不是你用你所想的数算的结果总比你想的数大15?不信你用其他的两位数试试细胞分裂问题细胞每次都是由一个分裂成两个。24816212223242n…我们曾经接触过“细胞分裂”问题:思路启迪 ? 可从具体的、简单的对折次数入手,寻找 所得折痕数与对折次数的变化关系. 13715…24816…212223242n2n-1 将一张长方形的纸对折,如右图所示可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折n次后,可以得到多少条折痕?折 纸 问 题谁能算出:1+2+22+23+24+……2n=?
13715…24816…212223242n2n-1观察上表可得: 1=21- 1 3=1+ 21 =22- 1
7=1+21 +22 =23- 1
15= 1+21 +22 +23=24- 1……所以 1+2+22+23+24+……2n=
2n+1-1+2+4+8探索规律的一般步骤:猜 想 规 律表 示 规 律验 证 规 律具 体 问 题观 察 特 例成立得出结论头 回新 重索 探智慧园1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 x 10 5 1
1 6 y 20 15 6 1
观察下表,找出规律:根据表中的规律,可知x = ,y = .1015等分次数(n)正方形个数(s)=3+1=2×3+1=3×3+1=4×3+1思维拓展
①根据上述规律你知道第2003次操作后能将原来的正方形纸板剪成多少个正方形纸板?
②请你推断,能不能按上述操作过程,将原来的正方形纸板剪成33个正方形?为什么?① S2003=3×2003 + 1=60101.观察下列各式,你会发现什么规律?
3×5=15,而15=42-1;
5×7=35,而35=62-1;
11×13=143,而143=122-1;
……
请你猜想到的规律用只含一个字母的式子表示出来: .2.观察下列顺序排列的等式:
9×0+1=1,
9×1+2=11,
9×2+3=21,
9×3+4=31,
9×4+5=41,
……
猜想:第n个等式(n为正整数)应为 .3.观察下列各式:
1×3=12+2×1,
2×4=22+2×2,
3×5=32+2×3,
……
请你将猜想到的规律用自然数n(n≥1)表示出来: .
