2023-2024学年八年级华东师大版数学上册 13.2.1和13.2.2 全等三角形及判定条件 同步练习(含答案)
文档属性
| 名称 | 2023-2024学年八年级华东师大版数学上册 13.2.1和13.2.2 全等三角形及判定条件 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 550.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 20:01:32 | ||
图片预览



文档简介
13.2.1和13.2.2 全等三角形及判定条件
一、单选题(每小题3分,共30分)
1.下列说法正确的是( )
A.全等三角形的周长和面积分别相等 B.全等三角形是指形状相同的两个三角形
C.全等三角形是指面积相等的两个三角形 D.所有的等边三角形都是全等三角形
2.如图,,C,B是对应点,下列结论错误的是( )
A.和是对应角 B.和是对应角
C.与是对应边 D.和是对应边
3.下列说法中正确的是( )
A.两个面积相等的三角形是全等三角形 B.三个对应角都相等的三角形是全等三角形
C.两个周长相等的三角形是全等三角形 D.两个完全重合的三角形是全等三角形
4.如图,,,,,则的度数为( )
A. B. C. D.
5.如图,和关于直线对称,连接,下列结论:
①l垂直平分;②;③;④直线的交点一定在上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.下列说法正确的是( )
A.两个直角三角形一定全等 B.形状相同的两个三角形全等
C.面积相等的两个三角形全等 D.全等三角形的面积一定相等
7.下列命题:①全等三角形的面积相等;②面积相等的两个三角形全等;③成轴对称的两个图形全等;④两个全等三角形是轴对称图形.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
8.下列命题:①形状相同的三角形是全等三角形;②面积相等的三角形是全等三角形;③全等三角形的周长相等;④经过平移或旋转得到的三角形与原三角形是全等三角形.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形 B.全等三角形的周长和面积分别相等
C.全等三角形是指面积相等的两个三角形 D.所有的直角三角形都是全等三角形
10.如图,,的延长线交于,,,,则的度数为 ( )
A. B. C. D.
二、填空题(每小题3分,共30分)
11.已知图中的两个三角形全等,则 °
12.已知的周长为,则 .
13.如图,,,,点P在线段上以的速度由点A向点B运动,同时,点Q在射线上运动速度为,它们运动的时间为(当点P运动结束时,点Q运动随之结束),当点P,Q运动到某处时,有与BPQ全等,此时 .
14.如图,已知△ABD≌△ACE,且∠BAD和∠CAE、∠ABD和∠ACE是对应角,则另一对对应角是 ,对应边是 , , .
15.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边: .
16.以下说法中,正确的是(填写序号) .
①周长相等的两个三角形全等;
②有两边及一角分别相等的两个三角形全等;
③两个全等三角形的面积相等;
④面积相等的两个三角形全等.
17.如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠AFE= °.
18.如图,已知AB=AC,D为∠BAC的角平分线上的一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上的两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上的三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第5个图形中有全等三角形的对数是 .
19.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠BAC=145°,则∠α= .
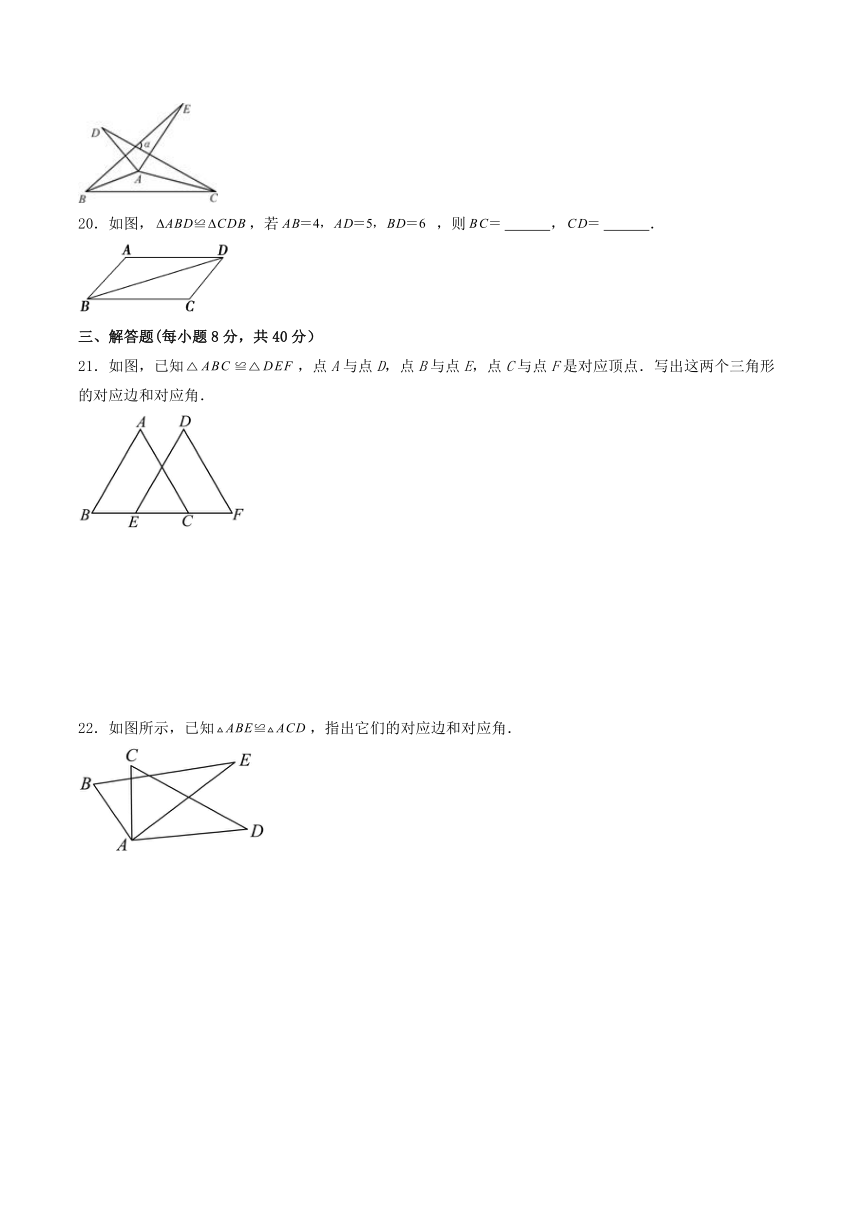
20.如图,,若 ,则 , .
三、解答题(每小题8分,共40分)
21.如图,已知,点A与点D,点B与点E,点C与点F是对应顶点.写出这两个三角形的对应边和对应角.
22.如图所示,已知,指出它们的对应边和对应角.
23.如图,,点D在边上,与交于点P,已知,,,.
(1)求的度数.
(2)求与的周长和.
24.(1)如图1,为直角三角形,,若沿图中虚线剪去,则__________;
(2)如图2,在中,,剪去后成为四边形,则__________;
(3)如图2,根据(1)和(2)的求解过程,请归纳与的关系是______________;
(4)若没有剪去,而是将折成如图3的形状,试探究与的关系,并说明理由.
25.如图,,写出两个全等三角形对应边及对应角.
参考答案
1.A 2.C 3.D 4.C 5.D 6.D 7.B 8.B 9.B 10.B
11. 12.5 13.或 14.∠ADB和∠AEC AB和AC AD和AE BD和CE
15.BC和BC,CD和CA,BD和AB 16.③ 17.85 18.15 19.70° 20. 5 4
21.【详解】解:∵,点A与点D,点B与点E,点C与点F是对应顶点,
∴这两个三角形的对应边是:和,和,和;
对应角是:和,和,和.
22.【详解】解:∵,
∴的对应边是,的对应边是,的对应边是,
的对应角是,的对应角是,的对应角是.
23.【详解】(1)解:∵,,
∴,
∵,
∴,
∴,
即的度数为;
(2)解:∵,
∴,,
∴与的周长和为
.
24.【详解】(1)为直角三角形,,
∴,
∵,,
∴,
∴,
故答案为:.
(2)∵,
∴,
∵,,
∴,
∴,
故答案为:.
(3)由(1)和(2)得,,
∵,
∴,
∴.
(4),理由见下:
由题意得,,
∴,,
∴,,
∴,
∵,
∴,
∴,
∴,
∴.
25.【详解】,
对应边为和,和,和,
对应角为和,和,和.
一、单选题(每小题3分,共30分)
1.下列说法正确的是( )
A.全等三角形的周长和面积分别相等 B.全等三角形是指形状相同的两个三角形
C.全等三角形是指面积相等的两个三角形 D.所有的等边三角形都是全等三角形
2.如图,,C,B是对应点,下列结论错误的是( )
A.和是对应角 B.和是对应角
C.与是对应边 D.和是对应边
3.下列说法中正确的是( )
A.两个面积相等的三角形是全等三角形 B.三个对应角都相等的三角形是全等三角形
C.两个周长相等的三角形是全等三角形 D.两个完全重合的三角形是全等三角形
4.如图,,,,,则的度数为( )
A. B. C. D.
5.如图,和关于直线对称,连接,下列结论:
①l垂直平分;②;③;④直线的交点一定在上,
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.下列说法正确的是( )
A.两个直角三角形一定全等 B.形状相同的两个三角形全等
C.面积相等的两个三角形全等 D.全等三角形的面积一定相等
7.下列命题:①全等三角形的面积相等;②面积相等的两个三角形全等;③成轴对称的两个图形全等;④两个全等三角形是轴对称图形.其中真命题有( )
A.1个 B.2个 C.3个 D.4个
8.下列命题:①形状相同的三角形是全等三角形;②面积相等的三角形是全等三角形;③全等三角形的周长相等;④经过平移或旋转得到的三角形与原三角形是全等三角形.其中是真命题的有( )
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形 B.全等三角形的周长和面积分别相等
C.全等三角形是指面积相等的两个三角形 D.所有的直角三角形都是全等三角形
10.如图,,的延长线交于,,,,则的度数为 ( )
A. B. C. D.
二、填空题(每小题3分,共30分)
11.已知图中的两个三角形全等,则 °
12.已知的周长为,则 .
13.如图,,,,点P在线段上以的速度由点A向点B运动,同时,点Q在射线上运动速度为,它们运动的时间为(当点P运动结束时,点Q运动随之结束),当点P,Q运动到某处时,有与BPQ全等,此时 .
14.如图,已知△ABD≌△ACE,且∠BAD和∠CAE、∠ABD和∠ACE是对应角,则另一对对应角是 ,对应边是 , , .
15.如图,△ABC≌△DBC,且∠A和∠D,∠ABC和∠DBC是对应角,其对应边: .
16.以下说法中,正确的是(填写序号) .
①周长相等的两个三角形全等;
②有两边及一角分别相等的两个三角形全等;
③两个全等三角形的面积相等;
④面积相等的两个三角形全等.
17.如图,△ABC≌△ADE,BC的延长线经过点E,交AD于F,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,则∠AFE= °.
18.如图,已知AB=AC,D为∠BAC的角平分线上的一点,连接BD,CD;如图2,已知AB=AC,D、E为∠BAC的角平分线上的两点,连接BD,CD,BE,CE;如图3,已知AB=AC,D、E、F为∠BAC的角平分线上的三点,连接BD,CD,BE,CE,BF,CF;…,依次规律,第5个图形中有全等三角形的对数是 .
19.如图,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠BAC=145°,则∠α= .
20.如图,,若 ,则 , .
三、解答题(每小题8分,共40分)
21.如图,已知,点A与点D,点B与点E,点C与点F是对应顶点.写出这两个三角形的对应边和对应角.
22.如图所示,已知,指出它们的对应边和对应角.
23.如图,,点D在边上,与交于点P,已知,,,.
(1)求的度数.
(2)求与的周长和.
24.(1)如图1,为直角三角形,,若沿图中虚线剪去,则__________;
(2)如图2,在中,,剪去后成为四边形,则__________;
(3)如图2,根据(1)和(2)的求解过程,请归纳与的关系是______________;
(4)若没有剪去,而是将折成如图3的形状,试探究与的关系,并说明理由.
25.如图,,写出两个全等三角形对应边及对应角.
参考答案
1.A 2.C 3.D 4.C 5.D 6.D 7.B 8.B 9.B 10.B
11. 12.5 13.或 14.∠ADB和∠AEC AB和AC AD和AE BD和CE
15.BC和BC,CD和CA,BD和AB 16.③ 17.85 18.15 19.70° 20. 5 4
21.【详解】解:∵,点A与点D,点B与点E,点C与点F是对应顶点,
∴这两个三角形的对应边是:和,和,和;
对应角是:和,和,和.
22.【详解】解:∵,
∴的对应边是,的对应边是,的对应边是,
的对应角是,的对应角是,的对应角是.
23.【详解】(1)解:∵,,
∴,
∵,
∴,
∴,
即的度数为;
(2)解:∵,
∴,,
∴与的周长和为
.
24.【详解】(1)为直角三角形,,
∴,
∵,,
∴,
∴,
故答案为:.
(2)∵,
∴,
∵,,
∴,
∴,
故答案为:.
(3)由(1)和(2)得,,
∵,
∴,
∴.
(4),理由见下:
由题意得,,
∴,,
∴,,
∴,
∵,
∴,
∴,
∴,
∴.
25.【详解】,
对应边为和,和,和,
对应角为和,和,和.
