2.3.4 两条平行直线间的距离 课件(共22张PPT)
文档属性
| 名称 | 2.3.4 两条平行直线间的距离 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 47.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-27 13:01:40 | ||
图片预览








文档简介
(共22张PPT)
2.3.4 两条平行直线间的距离
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1. 理解两条平行线间的距离公式的推导.
2.掌握量平行线的距离公式,能应用两平行线距离公式解决有关距离问题.
3. 通过两平行线距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力
01情景导入
PART ONE
复习导入
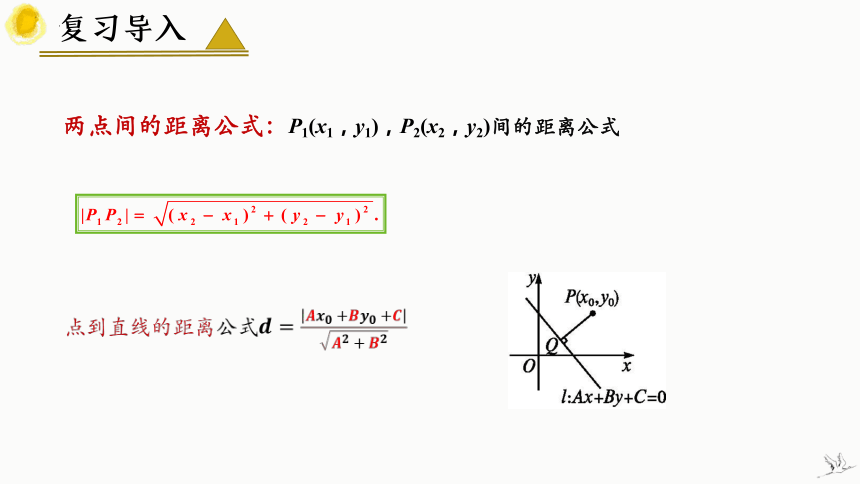
点到直线的距离公式
两点间的距离公式:P1(x1,y1),P2(x2,y2)间的距离公式
02两条平行线间的距离
PART ONE
两条平行线间的距离
两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长。
探究1:两条平行直线间的距离是指什么线段的长?
探究2:直线l1:x+y-1=0上有A(1,0)、B(0,1)、C(-1,2)三点,直线l2:x+y-2=0与直线l1平行,那么点A、B、C到直线l2的距离分别为多少?有什么规律吗?
A,B,C到直线l2距离分别为、.
距离均相等,平行线之间的距离处处相等.
两条平行线间的距离
探究3:已知两条平行直线l1Ax+By+C1=0(A,B不同时为0),
l2:Ax+By+C2=0(C2≠C1),如何求l1,l2间的距离?
根据两条平行直线间距离的含义,在直线上取任一点P,,点P到直线的距离就是直线与直线间的距离,这样求两条平行线间的距离就转化为求点到直线的距离。
即d=. 又Ax0+By0+C1=0,即Ax0+By0=-C1,
因此d=.
两条平行线间的距离
两条平行直线间的距离:
(1)概念:两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长.
(2)图示
(3)求法:两条平行直线间的距离转化为点到直线的距离.
(4)公式:两条平行直线l1Ax+By+C1=0与l2:Ax+By+C2=0间的距离
d=.
(2) 两直线方程中要求的系数要相同.
应用公式时注意:(1) 把直线方程要化成一般式;
两条平行线间的距离
公式应用时需要直线l1与直线l2中x,y的系数相同
两条平行线间的距离
3.已知直线l1:x+y-1=0,l2:2x+2y+a=0,且两直线间的距离为,则a=
-6或2
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
2
两条平行线间的距离
方法总结
两条平行线间的距离
4.两直线3x+y-3=0与6x+my+1=0平行,则它们之间的距离为( )
03两平行线距离应用
PART ONE
两平行线距离的应用
1.已知直线l与直线3x+4y-1=0平行,且两直线间的距离为4,则求直线l的方程.
解析:设所求的直线方程为3x+4y+C=0,
由题意得 =4,得C=19或C=-21.
∴直线l的方程为3x+4y+19=0或3x+4y-21=0.
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
4.求直线 关于直线 对称的直线 的方程.
解:由,解得, 的交点,
A 是直线 的点,它关于直线 的对称点为,则
解得 ,所以 ,则 M ,都在直线 上,所以 所在直线为 ,
故直线的方程为2x+11y+16=0.
5两条互相平行的直线分别过点A(6,2)和B(-3,-1),如果两条平行直线间的距离为d,求:
(1)d的变化范围;
(2)当d取最大值时,两条直线的方程.
【解析】(1)如图,当两条平行直线与AB垂直时,两平行直线间的距离最大,
为d=|AB|==3,
当两条平行线各自绕点B,A逆时针旋转时,距离逐渐变小,越来越接近于0,所以0(2)当d取最大值3时,两条平行线都垂直于AB,所以k==-=-3,
故所求的直线方程分别为y-2=-3(x-6)和y+1=-3(x+3),
即3x+y-20=0和3x+y+10=0.
两平行线距离的应用
04课堂小结
PART ONE
课堂小结
1.两平行线距离公式
2.两平行线距离公式的应用
2.3.4 两条平行直线间的距离
第 二 章 直线和圆的方程
人教A版2019选修第一册
学习目标
1. 理解两条平行线间的距离公式的推导.
2.掌握量平行线的距离公式,能应用两平行线距离公式解决有关距离问题.
3. 通过两平行线距离公式的探索和推导过程,培养学生运用等价转化、数形结合等数学思想方法解决问题的能力
01情景导入
PART ONE
复习导入
点到直线的距离公式
两点间的距离公式:P1(x1,y1),P2(x2,y2)间的距离公式
02两条平行线间的距离
PART ONE
两条平行线间的距离
两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长。
探究1:两条平行直线间的距离是指什么线段的长?
探究2:直线l1:x+y-1=0上有A(1,0)、B(0,1)、C(-1,2)三点,直线l2:x+y-2=0与直线l1平行,那么点A、B、C到直线l2的距离分别为多少?有什么规律吗?
A,B,C到直线l2距离分别为、.
距离均相等,平行线之间的距离处处相等.
两条平行线间的距离
探究3:已知两条平行直线l1Ax+By+C1=0(A,B不同时为0),
l2:Ax+By+C2=0(C2≠C1),如何求l1,l2间的距离?
根据两条平行直线间距离的含义,在直线上取任一点P,,点P到直线的距离就是直线与直线间的距离,这样求两条平行线间的距离就转化为求点到直线的距离。
即d=. 又Ax0+By0+C1=0,即Ax0+By0=-C1,
因此d=.
两条平行线间的距离
两条平行直线间的距离:
(1)概念:两条平行直线间的距离是指夹在这两条平行直线间的公垂线段的长.
(2)图示
(3)求法:两条平行直线间的距离转化为点到直线的距离.
(4)公式:两条平行直线l1Ax+By+C1=0与l2:Ax+By+C2=0间的距离
d=.
(2) 两直线方程中要求的系数要相同.
应用公式时注意:(1) 把直线方程要化成一般式;
两条平行线间的距离
公式应用时需要直线l1与直线l2中x,y的系数相同
两条平行线间的距离
3.已知直线l1:x+y-1=0,l2:2x+2y+a=0,且两直线间的距离为,则a=
-6或2
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
2
两条平行线间的距离
方法总结
两条平行线间的距离
4.两直线3x+y-3=0与6x+my+1=0平行,则它们之间的距离为( )
03两平行线距离应用
PART ONE
两平行线距离的应用
1.已知直线l与直线3x+4y-1=0平行,且两直线间的距离为4,则求直线l的方程.
解析:设所求的直线方程为3x+4y+C=0,
由题意得 =4,得C=19或C=-21.
∴直线l的方程为3x+4y+19=0或3x+4y-21=0.
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
两平行线距离的应用
4.求直线 关于直线 对称的直线 的方程.
解:由,解得, 的交点,
A 是直线 的点,它关于直线 的对称点为,则
解得 ,所以 ,则 M ,都在直线 上,所以 所在直线为 ,
故直线的方程为2x+11y+16=0.
5两条互相平行的直线分别过点A(6,2)和B(-3,-1),如果两条平行直线间的距离为d,求:
(1)d的变化范围;
(2)当d取最大值时,两条直线的方程.
【解析】(1)如图,当两条平行直线与AB垂直时,两平行直线间的距离最大,
为d=|AB|==3,
当两条平行线各自绕点B,A逆时针旋转时,距离逐渐变小,越来越接近于0,所以0
故所求的直线方程分别为y-2=-3(x-6)和y+1=-3(x+3),
即3x+y-20=0和3x+y+10=0.
两平行线距离的应用
04课堂小结
PART ONE
课堂小结
1.两平行线距离公式
2.两平行线距离公式的应用
